2023学苏科版数学七年级下学期期中考试模拟卷(1)【范围:第7~10章】
试卷更新日期:2023-04-12 类型:期中考试
一、单选题(每题3分,共24分)
-
1. 2022年9月9日下午,东阳市吉祥物“东迎迎”“向阳阳”正式发布.如图,通过平移吉祥物“向阳阳”可以得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列计算中,一定正确的是( )A、 B、 C、 D、3. 如图,点E在BA延长线上,下列条件不能判断的是( )
2. 下列计算中,一定正确的是( )A、 B、 C、 D、3. 如图,点E在BA延长线上,下列条件不能判断的是( ) A、 B、 C、 D、4. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 下列长度的两条线段与长度为6的线段能组成三角形的是( )A、1,4 B、3,3 C、4,6 D、2,46. 若a=0.32 , b=-3-2 , c=()-2 , d=()0 , 则( )A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b7. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=40°,则∠A的度数是( )
A、 B、 C、 D、4. 下列各式中,从左到右的变形是因式分解的是( )A、 B、 C、 D、5. 下列长度的两条线段与长度为6的线段能组成三角形的是( )A、1,4 B、3,3 C、4,6 D、2,46. 若a=0.32 , b=-3-2 , c=()-2 , d=()0 , 则( )A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b7. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=40°,则∠A的度数是( )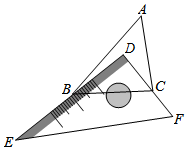 A、40° B、45° C、50° D、55°8. 已知 , ,…, 都是正数,如果 M=( + +…+ )( + +…+ ),N=( + +…+ )( + +…+ ),那么 M,N 的大小关系是( )A、M>N B、M=N C、M<N D、不确定
A、40° B、45° C、50° D、55°8. 已知 , ,…, 都是正数,如果 M=( + +…+ )( + +…+ ),N=( + +…+ )( + +…+ ),那么 M,N 的大小关系是( )A、M>N B、M=N C、M<N D、不确定二、填空题(每空3分,共33分)
-
9. 小明同学在百度搜索引擎中输入“中国梦,我的梦”,引擎搜索耗时0.000175秒,将这个数字用科学记数法表示为.10. 计算:.11. 若等腰三角形中有两边长分别是3和6,则这个三角形的周长为.12. 如图,∠1、∠2、∠3、∠4是五边形的外角,若∠A=120°,则∠1+∠2+∠3+∠4= .
 13. 若 , 则的结果为.14. 如果 , , 则 .15. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.
13. 若 , 则的结果为.14. 如果 , , 则 .15. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于.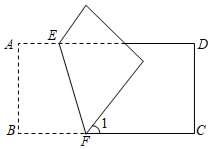 16. 已知展开式中不含项,且的系数为2.则的值为 .17. 如图, , 平分 , 平分 ,若设 , 则 度 用 , 的代数式表示 ,若 平分 , 平分 ,可得 , 平分 , 平分 ,可得 ,依次平分下去,则 度
16. 已知展开式中不含项,且的系数为2.则的值为 .17. 如图, , 平分 , 平分 ,若设 , 则 度 用 , 的代数式表示 ,若 平分 , 平分 ,可得 , 平分 , 平分 ,可得 ,依次平分下去,则 度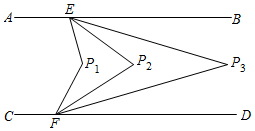 18. 若方程是二元一次方程,则.
18. 若方程是二元一次方程,则.三、解答题(共10题,共93分)
-
19. 计算:(1)、 .(2)、 .20. 先化简,再求值:(2a-3b)2-(2a+3b)(2a-3b)+6b(a-3b).其中a= 6,b= .21. 解方程组:(1)、;(2)、.22. 把下列各式分解因式;(1)、;(2)、 .23. 如图,方格纸中每一个小方格的边长为1个单位,△ABC的顶点都在方格纸的格点上.
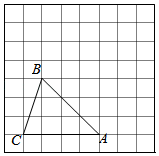 (1)、画出将△ABC向右平移2个单位,再向上平移3个单位得到的△A1B1C1(点A1、B1、C1分别是点A、B、C的对应点);(2)、连接AA1、BB1 , 则线段AA1、BB1的位置关系为;(3)、试在边AC上确定点P,连接BP,使BP平分△ABC的面积(要求:在图中画出线段BP).24. 如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
(1)、画出将△ABC向右平移2个单位,再向上平移3个单位得到的△A1B1C1(点A1、B1、C1分别是点A、B、C的对应点);(2)、连接AA1、BB1 , 则线段AA1、BB1的位置关系为;(3)、试在边AC上确定点P,连接BP,使BP平分△ABC的面积(要求:在图中画出线段BP).24. 如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
证明:∵AB⊥BF,CD⊥BF(已知),
∴∠ABD=∠CDF= ( ),
∴ ( )
∵∠1=∠2(已知),
∴ ( )
∴ ( )
∴∠3=∠E( )
25. 如图,已知EFAB,∠DEF=∠A.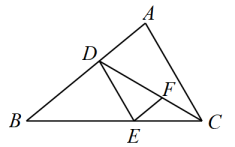 (1)、求证:DEAC;(2)、若CD平分∠ACB,∠BED=60°,求∠ACD的度数.26. 阅读:已知 , ,求 的值.
(1)、求证:DEAC;(2)、若CD平分∠ACB,∠BED=60°,求∠ACD的度数.26. 阅读:已知 , ,求 的值.解: , ,
.
请你根据上述解题思路解答下面问题:
(1)、已知 , ,求 的值.(2)、已知 ,求 的值.27. 提出问题:怎么运用矩形面积表示(y+2)(y+3)与2y+5的大小关系(其中y>0)?几何建模:
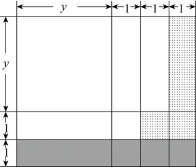
(1)画长y+3,宽y+2的矩形,按图方式分割
(2)变形:2y+5=(y+2)+(y+3)
(3)分析:图中大矩形的面积可以表示为(y+2)(y+3);阴影部分面积可以表示为(y+3)×1,画点部分的面积可表示为y+2,由图形的部分与整体的关系可知:(y+2)(y+3)>(y+2)+(y+3),即(y+2)(y+3)>2y+5
归纳提炼:
当a>2,b>2时,表示ab与a+b的大小关系.根据题意,设a=2+m,b=2+n(m>0,n>0),要求参照上述研究方法,画出示意图,并写出几何建模步骤(用铅笔画图,并标注相关线段的长)
28. “公路村村通”的政策让公路修到了山里,蜿蜒的盘山公路沟通了山里与外面的世界.数学活动课上,老师把山路抽象成图1所示的样子,并提出了以下问题:如图1,// , 点在直线、之间.求证: .

小贤的解法如下:
解:如图1,过点作EF∥AB.
因为 , 所以 .
因为 , 所以 .
因为 , 所以(根据1),
所以 ,
即 .
(1)、材料中的根据1是指 .(2)、若把图1变为图2,其中 , , , , 求的度数.(3)、如图3, , 是内部一点,且 , 延长与交于点 , , 且 . 已知 , 则的度数为(用含的式子表示).