2023学苏科版数学八年级下学期期中考试模拟卷（1）【范围：第7-10章】

试卷更新日期：2023-04-12 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共24分）

1. 下列图形中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件是随机事件的是（）

A、射击运动员射击一次，命中靶心 B、在标准大气压下，通常加热到 $100 ℃$ 时，水沸腾 C、任意画一个三角形，其内角和等于 $180 °$ D、在空旷的操场，向空中抛一枚硬币，硬币不会从空中落下

查看试题解析
3. 下列命题中真命题是（）

A、对角线互相垂直的四边形是菱形 B、矩形的四条边相等 C、对角线相等的四边形是矩形 D、菱形的对角线互相垂直

查看试题解析
4. 某校为了了解学生在校吃午餐所需的时间，抽查了20名学生在校吃午餐所需的时间，获得数据（单位： $m i n$ ）：10，12，15，10，16，18，19，18，20，18，18，20，28，22，31，20，15，16，21，16．若将这些数据以 $4 m i n$ 为组距进行分组，则组数是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 把分式 $\frac{2 x + y}{5 x y - y^{2}}$ 中的x，y的值都扩大为原来的8倍，则分式的值（）

A、不变 B、为原分式值的 $\frac{1}{8}$ C、为原分式值的8倍 D、为原分式值的 $\frac{1}{64}$

查看试题解析
6. 如图， $△ A B C$ 中，AB=10，AC=7，BC=9，点D、E、F分别是AB、AC、BC的中点，则四边形DBFE的周长是（）

A、13 B、 $\frac{19}{2}$ C、17 D、19

查看试题解析
7. 如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点E，AF交CD于点F，连接EF．若DF＝3，则BE的长为（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，分别以AB，AC，BC为边向△ABC外作正方形ABED，正方形ACHI，正方形BCGF．直线ED，HI交于点J，过点F作KF // HI，交DE于点K，过点G作GM // DE，与HI，KF分别交于点M，L. 则四边形KLMJ的面积为（）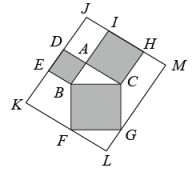

A、90 B、100 C、110 D、120

查看试题解析

二、填空题（每题3分，共30分）

9. 化简 $\frac{a^{2} - 4}{a + 2}$ 的结果是．

查看试题解析
10. 样本的50个数据分别落在4个组内，第1、2、3组数据的个数分别是7、8、15，则落在第4组数据的频数为．

查看试题解析
11. 若分式 $\frac{2}{x - 1}$ 的值为负数，则x的取值范围是．

查看试题解析
12. 如图，菱形ABCD中， $A B = 10$ ， AC，BD交于点O，若E是边AD的中点，∠AEO＝ $32 °$ ，则OE的长等于， ∠ADO的度数为.

查看试题解析
13. 如果 $\frac{a}{b} = 2$ ，则 $\frac{a^{2} - 2 a b + b^{2}}{a^{2} - b^{2}}$ = ．

查看试题解析
14. 一个矩形的一条对角线长为8，两条对角线的一个交角为120°，这个矩形的较长边等于.

查看试题解析
15. 如图 1 ，菱形纸片 $A B C D$ 的面积为 $30 c m^{2}$ ，对角线 $A C$ 的长为 $6 c m$ ，将这个菱形纸片沿对角线剪开，得到四个全等的直角三角形，将这四个直角三角形按图2 所示的方法拼成正方形．则大正方形中空白小正方形的边长是 $c m$ ．

查看试题解析
16. 如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有次.

查看试题解析
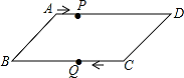17. 如图，将n个边长都为1cm的正方形按如图所示摆放，点A1， A2，…，An分别是正方形的中心，则n个正方形重叠形成的重叠部分的面积和为

查看试题解析
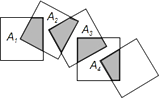18. 如图，在平面直角坐标系中，已知菱形OABC的顶点O、B的坐标分别为（0，0）、（2，2），若菱形绕点O逆时针旋转135°时，菱形的对角线交点D的坐标为．

查看试题解析

三、计算题（共2题，共16分）

19. 计算与化简：

(1)、 $(x y - x^{2}) \div \frac{x - y}{x y}$ ；

(2)、 $\frac{a^{2}}{a - 1} - a - 1$ .

(3)、先化简 $\frac{2 a + 2}{a - 1} \div (a + 1) + \frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后a在－1、1、2三个数中任选一个你喜欢的数代入求值.

查看试题解析
20. 解分式方程： $\frac{3}{x - 3} - \frac{1}{x + 3} = \frac{18}{x^{2} - 9}$

查看试题解析

四、作图题（共8分）

21. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C都是格点.

⑴将△ABC向左平移6个单位长度得到△A₁B₁C₁；

⑵将△ABC绕点O按逆时针方向旋转180°得到△A₂B₂C₂ ，请画出△A₂B₂C₂；

⑶若点B的坐标为（3，3）；写出△A₁B₁C₁与△A₂B₂C₂的对称中心的坐标 ▲ .

查看试题解析

五、解答题（共7题，共72分）

22. 第24届冬季奥林匹克运动会，即2022年北京冬季奥运会，将于2022年2月4日开幕，共设7个大项，15个分项，109个小项.学校从七年级同学中随机抽取若干名，组织了奥运知识竞答活动，将他们的成绩进行整理，得到如下不完整的频数分布表、频数分布直方图与扇形统计图.（满分为100分，将抽取的成绩分成A，B，C，D四组，每组含最大值不含最小值）
分组
频数
A：60～70
4
B：70～80
12
C：80～90
16
D：90～100
△

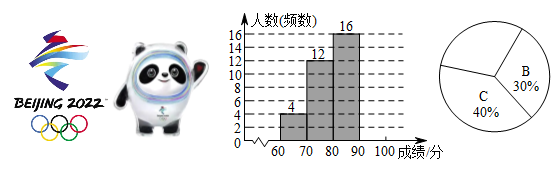(1)、本次知识竞答共抽取七年级同学名，D组成绩在扇形统计图中对应的圆心角为°；

(2)、请将频数分布直方图与扇形统计图补充完整；

(3)、学校将此次竞答活动的D组成绩记为优秀，已知该校初、高中共有学生2400名，小敏想根据七年级竞答活动的结果，估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.

查看试题解析
23. 随着通讯技术迅猛发展，人与人之间的沟通方式更多样，更便捷.为此，老师设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种）.某校八年级（1）班同学利用课余时间对全校师生进行了抽样调查，并将统计结果绘制成如图所示两幅不完整的统计图：

请结合图中所给的信息解答下列问题：

(1)、这次参与调查的共有人，在扇形统计图中，表示“微信”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、如果该校有3600人在使用手机：
①请估计该校最喜欢用“微信”进行沟通的人数；

②在该校师生中随机抽取一人，用频率估计概率，抽取的恰好使用“QQ”的概率是 ▲ .

查看试题解析
24. 如图，O为矩形ABCD对角线的交点，DE//AC，CE//BD.

(1)、求证：四边形OCED是菱形.

(2)、若AB=6，BC=8，求四边形OCED的周长.

查看试题解析
25. 如图，已知正方形ABCD的边长为3，菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上，AH=1，连接CF.

(1)、当DG=1时，求证：菱形EFGH为正方形；

(2)、设DG= $x$ ，请用含 $x$ 的代数式表示△FCG的面积；

查看试题解析
26. 观察下面的变形规律： $\frac{1}{1 \times 2} = \frac{1}{1} - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ；…，解答下面的问题：

(1)、若n为正整数，且写成上面式子的形式，请你猜想 $\frac{1}{n (n + 1)} =$ .

(2)、说明你猜想的正确性.

(3)、计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2018 \times 2019} =$ .

(4)、解关于n的分式方程 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)} = \frac{n + 7}{n + 9}$ .

查看试题解析
27. 如图，点 $E$ 在正方形 $A O C D$ 的边 $A D$ 上，点 $H$ 在边 $A O$ 上， $D H ⊥ C E$ .

(1)、如图1，求证： $A H = D E$ ；

(2)、如图2， $E F ⊥ C E$ ， $F H ⊥ A O$ ，垂足分别为 $E$ ， $H$ ，求证： $F H = A H$ ；

(3)、在（2）的条件下，连接 $C F$ ， $T$ 为 $F C$ 的中点，若 $F O = 10$ ， $T O = 4 \sqrt{2}$ ，求点 $E$ 的坐标.

查看试题解析
28. 已知，矩形ABCD中，AB＝4cm，BC＝8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．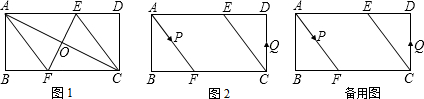

(1)、如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

(2)、如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．

查看试题解析

分组	频数
A：60～70	4
B：70～80	12
C：80～90	16
D：90～100	△