2023年北师大版数学七年级下学期期中考试模拟试卷(2)【范围:1-4章】
试卷更新日期:2023-04-12 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 如图所示,∠1和∠2是对顶角的是( )A、
 B、
B、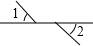 C、
C、 D、
D、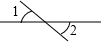 2. 下列计算正确的是( )A、 B、 C、 D、3. 若 , , 则的值为( )A、1 B、2 C、3 D、-34. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,5cm D、3cm,4cm,8cm5. 如图所示,工人师傅在砌门时,通常用木条固定长方形门框 , 使其不变形,这样做的数学根据是( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 若 , , 则的值为( )A、1 B、2 C、3 D、-34. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,5cm D、3cm,4cm,8cm5. 如图所示,工人师傅在砌门时,通常用木条固定长方形门框 , 使其不变形,这样做的数学根据是( )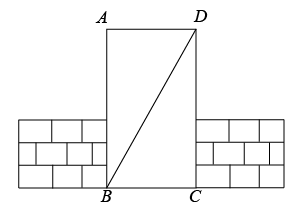 A、两点确定一条直线 B、两点之间,线段最短 C、同角的余角相等 D、三角形具有稳定性6. 如图,下列条件中不能判定AB∥CD的是( )
A、两点确定一条直线 B、两点之间,线段最短 C、同角的余角相等 D、三角形具有稳定性6. 如图,下列条件中不能判定AB∥CD的是( )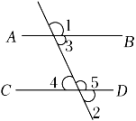 A、∠1=∠2 B、∠3=∠4 C、∠3+∠5=180° D、∠2=∠37. 根据实验结果表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下表的关系,下列说法错误的是( )
A、∠1=∠2 B、∠3=∠4 C、∠3+∠5=180° D、∠2=∠37. 根据实验结果表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下表的关系,下列说法错误的是( )0
1
2
3
4
20
21
22
23
24
A、与都是变量,且是自变量,是因变量 B、弹簧不挂重物时的长度为 C、随着所挂物体重量的增加,弹簧长度逐渐变长 D、所挂物体的重量每增加 , 弹簧长度增加8. 如图,向高为H的圆柱形空水杯中注水,表示注水量y与水深x的关系的图象是下面哪一个?( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是( )
9. 如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是( ) A、30° B、20° C、40° D、15°10. 南宋数学家杨辉在其著作《详解九章算法》中揭示了(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将图称为“杨辉三角”.
A、30° B、20° C、40° D、15°10. 南宋数学家杨辉在其著作《详解九章算法》中揭示了(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将图称为“杨辉三角”.……

则展开式中所有项的系数和是( )
A、128 B、256 C、512 D、1024二、填空题(每空3分,共15分)
-
11. 如图所示的是一款手机支架,能非常方便地支起手机,由图分析这款手机支架的设计原理是三角形的 .
 12. 若是一个完全平方式,则k的值为 .13. 如图,在中, , 点D是边上一动点,若 , , , 则的面积S与x之间的关系式为 .
12. 若是一个完全平方式,则k的值为 .13. 如图,在中, , 点D是边上一动点,若 , , , 则的面积S与x之间的关系式为 . 14. 如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和 , 过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 .
14. 如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和 , 过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 . 15. 某物流公司的快递车和货车每天沿同一条路线往返于A、B两地,快递车比货车多往返一趟.如图所示,表示货车距离A地的路程y(单位:h)与所用时间x(单位h)的图象,其间在B地装卸货物2h.已知快递车比货车早1h出发,最后一次返回A地比货车晚1h.若快递车往返途中速度不变,且在A、B两地均不停留,则两车在往返途中相遇的次数为次.
15. 某物流公司的快递车和货车每天沿同一条路线往返于A、B两地,快递车比货车多往返一趟.如图所示,表示货车距离A地的路程y(单位:h)与所用时间x(单位h)的图象,其间在B地装卸货物2h.已知快递车比货车早1h出发,最后一次返回A地比货车晚1h.若快递车往返途中速度不变,且在A、B两地均不停留,则两车在往返途中相遇的次数为次.
三、解答题(共7题,共55分)
-
16. 先化简,再求值:
, 其中、满足.
17. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数. 18. 如图,AB∥CD,∠1=∠2.
18. 如图,AB∥CD,∠1=∠2. (1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.19.(1)、填空:
(1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.19.(1)、填空:;
;
;
……
.
(2)、猜想:(其中n为正整数,且 .
(3)、利用(2)中猜想的结论计算: .20. 如图,在△ABC中,AD为BC边上的高,BC=8,AD=4,点P为边BC上一动点,连接AP,随着BP长度的变化,△ACP的面积也在变化. (1)、在这个变化过程中,自变量是什么?因变量是什么?(2)、若设BP=x,△ACP的面积为y,请写出y与x的关系式;(3)、当BPAD时,求△ACP的面积.21. 图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)、在这个变化过程中,自变量是什么?因变量是什么?(2)、若设BP=x,△ACP的面积为y,请写出y与x的关系式;(3)、当BPAD时,求△ACP的面积.21. 图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.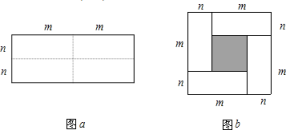 (1)、请用两种不同的方法,求图b中阴影部分的面积:
(1)、请用两种不同的方法,求图b中阴影部分的面积:方法1:; 方法2:;
(2)、观察图b,写出代数式 , , 之间的等量关系,并通过计算验证;(3)、根据(2)题中的等量关系,解决如下问题:若 , , 求的值.22. 如图1,已知直线 , 点A在直线PQ上,点B,C在直线MN上,连接AB,AC, , , AD平分 , BD平分 , AD与BD相交于点D. (1)、求的度数;(2)、若将图1中的线段AC沿MN向右平移到 , 如图2,此时平分 , 平分 , 与BD相交于点D, , , 求的度数;(3)、若将图1中的线段AC沿MN向左平移到 , 如图3,其他条件与(2)相同,求此时的度数.
(1)、求的度数;(2)、若将图1中的线段AC沿MN向右平移到 , 如图2,此时平分 , 平分 , 与BD相交于点D, , , 求的度数;(3)、若将图1中的线段AC沿MN向左平移到 , 如图3,其他条件与(2)相同,求此时的度数.