2023年北师大版数学七年级下学期期中考试模拟试卷(1)【范围:1-4章】
试卷更新日期:2023-04-12 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 计算(﹣x3)2的结果是( )A、x5 B、x6 C、﹣x5 D、﹣x62. 华为作为世界顶级科技公司,设计的麒麟90005GSoc芯片,拥有领先的5nm制程和架构设计,5nm=0.000000005m,将0.000000005用科学记数法表示为( )A、5×10﹣7 B、5×10﹣8 C、5×10﹣9 D、5×10﹣103. 在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是( )A、
 B、
B、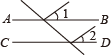 C、
C、 D、
D、 4. 如图,已知△ABC≌△DEF,则下列结论不正确的是( )
4. 如图,已知△ABC≌△DEF,则下列结论不正确的是( ) A、∠A=∠D B、∠C=∠E C、AB=DE D、BC=EF5. 在下列的计算中正确的是( )A、2x+3y=5xy B、(a+2)(a-2)=a2+4 C、a2•ab=a3b D、(x-3)2=x2+6x+96. 将一副直角三角板按如图所示的方式叠放在一起,若AC∥DE,则∠BAE的度数为( )
A、∠A=∠D B、∠C=∠E C、AB=DE D、BC=EF5. 在下列的计算中正确的是( )A、2x+3y=5xy B、(a+2)(a-2)=a2+4 C、a2•ab=a3b D、(x-3)2=x2+6x+96. 将一副直角三角板按如图所示的方式叠放在一起,若AC∥DE,则∠BAE的度数为( )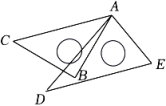 A、50° B、65° C、75° D、85°7. 若 的值使得 成立,则 的值为( )A、5 B、4 C、3 D、28. 如下图(1),边长为a的大正方形中一个边长为b的小正方形,小明将图(1)的阴影部分拼成了一个矩形,如图(2).这一过程可以验证( )
A、50° B、65° C、75° D、85°7. 若 的值使得 成立,则 的值为( )A、5 B、4 C、3 D、28. 如下图(1),边长为a的大正方形中一个边长为b的小正方形,小明将图(1)的阴影部分拼成了一个矩形,如图(2).这一过程可以验证( ) A、a2+b2-2ab=(a-b)2 B、a2+b2+2ab=(a+b)2 C、2a2-3ab+b2=(2a-b)(a-b) D、a2-b2=(a+b) (a-b)9. 如图,中,是边上的中线, , , 那么和的周长的差是( )
A、a2+b2-2ab=(a-b)2 B、a2+b2+2ab=(a+b)2 C、2a2-3ab+b2=(2a-b)(a-b) D、a2-b2=(a+b) (a-b)9. 如图,中,是边上的中线, , , 那么和的周长的差是( )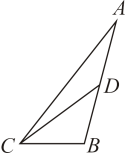 A、 B、 C、 D、10. 如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中符合题意结论的个数是( )
A、 B、 C、 D、10. 如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中符合题意结论的个数是( )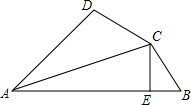 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共15分)
-
11. 已知 , , 则 .12. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为三角形ACE的面积为有y,则y与x的关系式为.
 13. 若 , , 则 .14. 如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明 .
13. 若 , , 则 .14. 如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明 . 15. 如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转.
15. 如图,∠A=70°,O是AB上一点,直线OD与AB所夹的∠AOD=100°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转.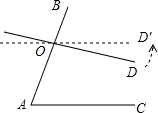
三、解答题(共7题,共55分)
-
16. 利用乘法公式计算:(1)、(2)、17. 先化简,再求值:
, 其中、满足.
18. 完成下面的证明.如图, , 分别在和上, , 与互余,于点.求证.

证明:∵(已知),
∴(垂直的定义).
∵(已知),
∴ ∥ ( ).
∴( ).
又∵(已知),
(平角的定义),
∴.
∴ .
∴( ).
19. 已知:如图,△ABC.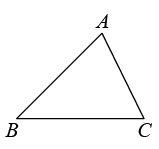
 (1)、求作:△DEF,使△DEF≌△ABC(要求:在指定区域尺规作图,不写作法,保留作图痕迹);(2)、根据作图过程写出△DEF≌△ABC的依据: .20. 晚上7点15分,小李骑自行车从家出发到距离家3500米远的水上公园看7点40分开始的水上灯光秀,如图所示是小李从家到公园路途中离家的距离与离家时间之间的关系.
(1)、求作:△DEF,使△DEF≌△ABC(要求:在指定区域尺规作图,不写作法,保留作图痕迹);(2)、根据作图过程写出△DEF≌△ABC的依据: .20. 晚上7点15分,小李骑自行车从家出发到距离家3500米远的水上公园看7点40分开始的水上灯光秀,如图所示是小李从家到公园路途中离家的距离与离家时间之间的关系.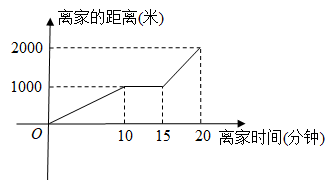 (1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?
(1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?