2023年北师大版数学八年级下学期期中模拟试卷（2）（范围：1~3章）

试卷更新日期：2023-04-12 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若x＞y，则下列不等式成立的是（）

A、x＋5＞y＋5 B、 $\frac{1}{3}$ x＜ $\frac{1}{3}$ y C、－8x＞－8y D、x－10＞y＋10

查看试题解析
3. 等腰三角形的一个角是50°，则它的底角是（　　）

A、50° B、50°或65° C、80°或50° D、65°

查看试题解析
4. 由线段a，b，c组成的三角形是直角三角形的是（）

A、 $a = 2$ ， $b = 4$ ， $c = 5$ B、 $a = \sqrt{3}$ ， $b = \sqrt{4}$ ， $c = \sqrt{5}$ C、 $a = 3$ ， $b = 4$ ， $c = 5$ D、 $a = 5$ ， $b = 13$ ， $c = 14$

查看试题解析
5. 如图，已知AB＝AC＝7，BC＝5，以A，B两点为圆心，大于 $\frac{1}{2}$ AB的长为半径画圆弧，两弧相交于点M，N，连接MN与AC相交于点D，则△BCD的周长是（　　）

A、12 B、14 C、15 D、17

查看试题解析
6. 如图，在△ABC中，∠ACB＝90°，BE平分ABC，DE⊥AB于点D，如果AC＝7cm，DE＝3cm，那么AE等于（）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
7. 若关于x的不等式组 ${\begin{array}{l} x - 2 \leq 3 a \\ x + 4 > a \end{array}$ 无解，则a的取值范围是（）

A、 $a$ ≤－3 B、 $a < - 3$ C、 $a > 3$ D、 $a$ ≥3

查看试题解析
8. 如图，在平面直角坐标系中，等边△OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（）

A、（4，2 $\sqrt{3}$ ） B、（3，3） C、（4，3） D、（3，2）

查看试题解析
9. 如图，直线y＝x＋m与y＝nx－5n（n≠0）的交点的横坐标为3，则关于x的不等式x＋m＞nx－5n＞0的整数解为（）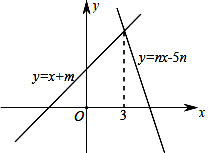

A、6 B、5 C、4 D、3

查看试题解析
10. 如图，点C为线段AE上一动点（不与点A、E重合），在AE同侧分别作等边ΔABC和等边ΔCDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，以下结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOE=120°；⑥ΔCPQ为等边三角形；⑦CO平分∠AOE；正确的有（）个．

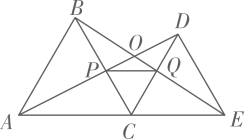A、3个 B、5个 C、6个 D、7个

查看试题解析

二、填空题（每空3分，共15分）

11. 已知点A（-1，2）与点B（3，4）是成中心对称的图形上的两个对称点，则对称中心的坐标为。

查看试题解析
12. 如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α.以OC为一边作等边三角形OCD，连接AD，当△AOD是等腰三角形时，求α的角度为

查看试题解析
13. 某个一元一次不等式组中的两个不等式的解集在同一条数轴上表示如图所示，则该不等式组的解集为．

查看试题解析
14. 某主题公园内一个活动项目的收费标准如下：个人票，每张10元；团体票，满20张八折优惠.当人数为时(人数不到20人)，买20人的团体票反而合算.

查看试题解析
15. 如图，在△ABC中，AB=3，AC=5，AD是BC边上的中线，且AD=2，则BC的长为.

查看试题解析

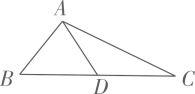
三、计算题（共8分）

16. 解不等式（组）：

(1)、3x﹣2<x+10；

(2)、 ${\begin{array}{l} 2 (x - 3) + 8 > x \\ \frac{3 x + 1}{4} \geq 2 x - 1 \end{array}$ ．

查看试题解析

四、作图题（共9分）

17. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 3 ， 5) ， B (- 2 ， 1) ， C (- 1 ， 3)$

(1)、若 $△ A B C$ 经过平移后得到 $△ A_{1} B_{1} C_{1}$ ，已知点 $C_{1}$ 的坐标为 $(- 1 ， - 3)$ ，画出平移后的图形，并写出顶点 $A_{1} ， B_{1}$ 的坐标；

(2)、画出 $△ A_{2} B_{2} C_{2}$ ， $△ A B C$ 和 $△ A_{2} B_{2} C_{2}$ 关于坐标原点O成中心对称图形，并写出顶点 $A_{2} ， B_{2}$ 的坐标；

(3)、将 $△ A B C$ 绕着点O按顺时针方向旋转 $90 °$ 得到 $△ A_{3} B_{3} C_{3}$ ，画出 $△ A_{3} B_{3} C_{3}$ ，并写出 $△ A_{3} B_{3} C_{3}$ 的各顶点的坐标．

查看试题解析

五、解答题（共5题，共38分）

18. 如图，在△ABC中，∠B=40°，∠C=50°．

(1)、通过观察尺规作图的痕迹，可以发现直线DF是线段AB的，射线AE是∠DAC的．

(2)、求∠DAE的度数．

查看试题解析
19. 如图，在△ABC中，点D是BC边上一点，连接AD，若AB＝10，AC＝17，BD＝6，AD＝8.

(1)、求证：△ABD是直角三角形；

(2)、求BC的长.

查看试题解析
20. 在 $△ A B C$ 中， $A B = A C$ ， $B D$ 是 $△ A B C$ 的角平分线

(1)、如图1，当 $∠ A = 36 °$ 时，求证： $A D = B C$ ；

(2)、如图2，若 $∠ A = 90 °$ ，且 $A B = 1$ ，求 $A D$ 的长；

(3)、如图3，当 $∠ A = 100 °$ 时，求证： $A D + B D = B C$ .

查看试题解析
21. 2021年11月，我市政府紧急组织一批物资送往新冠疫情高风险地区，现已知这批物资中，食品和矿泉水共410箱，且食品比矿泉水多110箱．

(1)、求食品和矿泉水各有多少箱；

(2)、现计划租用A，B两种货车共10辆，一次性将所有物资送到群众手中，已知A种货车最多可装食品40箱和矿泉水10箱，B种货车最多可装食品20箱和矿泉水20箱，试通过计算帮助政府设计几种运输方案；

(3)、在（2）的条件下，A种货车每辆需付运费600元，B种货车每辆需付运费450元，政府应该选哪种方案，才能使运费最少？最少运费是多少？

查看试题解析
22. 如图

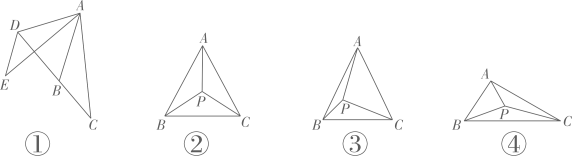(1)、【操作发现】如图①，将△ABC绕点A顺时针旋转60°，得到△ADE，连接BD，则∠ABD=度；

(2)、【类比探究】如图②，在等边三角形ABC内任取一点P，连接PA，PB，PC，求证：以PA，PB，PC的长为三边必能组成三角形；

(3)、【解决问题】如图③，在边长为 $\sqrt{7}$ 的等边三角形ABC内有点P，∠APC=90°，∠BPC=120°，求△APC的面积；

(4)、【拓展应用】如图④是A，B，C三个村子位置的平面图，经测量，AC=4，BC=5，∠ACB=30°，P为△ABC内的一个动点，连接PA，PB，PC，求PA+PB+PC的最小值．

查看试题解析