2023年北师大版数学八年级下学期期中模拟试卷(1)(范围:1~3章)
试卷更新日期:2023-04-12 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若m>n,则下列不等式正确的是( )A、m-2<n-2 B、am>an C、-8m>-8n D、3. 在平面直角坐标系内,将M(6,2)先向左平移4个单位,再向下平移2个单位,则移动后的点的坐标是 ( )A、(2,0) B、(10,4) C、(10,0) D、(2,4)4. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( )
2. 若m>n,则下列不等式正确的是( )A、m-2<n-2 B、am>an C、-8m>-8n D、3. 在平面直角坐标系内,将M(6,2)先向左平移4个单位,再向下平移2个单位,则移动后的点的坐标是 ( )A、(2,0) B、(10,4) C、(10,0) D、(2,4)4. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM的一个动点,若PA=4,则PQ的最小值为( ) A、 B、2 C、4 D、5. 下列命题中,假命题的是( )A、等腰三角形的两个底角相等 B、直角三角形的两个锐角互余 C、有两个内角是 60°的三角形是等边三角 D、等腰三角形的两个底角的平分线互相垂直6. 如图,在△ABC中, , AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,且 , 则AB的长为( )
A、 B、2 C、4 D、5. 下列命题中,假命题的是( )A、等腰三角形的两个底角相等 B、直角三角形的两个锐角互余 C、有两个内角是 60°的三角形是等边三角 D、等腰三角形的两个底角的平分线互相垂直6. 如图,在△ABC中, , AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,且 , 则AB的长为( ) A、6 B、5.5 C、5 D、47. 如图,在△ABC中,点P在边BC上(不与点B,点C重合) ,下列说法正确说法正确的是( )
A、6 B、5.5 C、5 D、47. 如图,在△ABC中,点P在边BC上(不与点B,点C重合) ,下列说法正确说法正确的是( ) A、若∠BAC=90°,∠BAP=∠B,则AC=PC B、若∠BAC=90°,∠BAP=∠C,则AP⊥BC C、若AP⊥BC,PB=PC,则∠BAC=90° D、若PB=PC,∠BAP=∠CAP,则∠BAC=90°8. 如图,△ABC是等边三角形,且AD=BE=CF,则△DEF是( )
A、若∠BAC=90°,∠BAP=∠B,则AC=PC B、若∠BAC=90°,∠BAP=∠C,则AP⊥BC C、若AP⊥BC,PB=PC,则∠BAC=90° D、若PB=PC,∠BAP=∠CAP,则∠BAC=90°8. 如图,△ABC是等边三角形,且AD=BE=CF,则△DEF是( )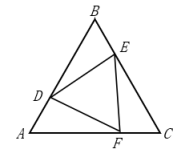 A、等边三角形 B、等腰三角形 C、钝角三角形 D、直角三角形9. 若关于x的不等式组的整数解共有2个,则m的取值范围是( )A、5<m≤6 B、4<m≤5 C、5≤m<6 D、4≤m<510. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
A、等边三角形 B、等腰三角形 C、钝角三角形 D、直角三角形9. 若关于x的不等式组的整数解共有2个,则m的取值范围是( )A、5<m≤6 B、4<m≤5 C、5≤m<6 D、4≤m<510. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( ) A、8 B、7 C、6 D、5
A、8 B、7 C、6 D、5二、填空题(每空3分,共15分)
-
11. 等腰三角形的顶角度数为 , 则它的底角度数为 .12. 如图,△DEC与△ABC关于点C成中心对称,AB=3,AC=1,∠D=90°,则AE的长是 .
 13. 直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
13. 直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .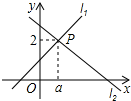 14. 如图,在△ABC中,AC=24,AB=25,BC=7.在AB上取一点E,AC上取一点F,连接EF,若∠EFC=125°,过点B作BD∥EF,且点D在AB的右侧,则∠CBD的度数为 .
14. 如图,在△ABC中,AC=24,AB=25,BC=7.在AB上取一点E,AC上取一点F,连接EF,若∠EFC=125°,过点B作BD∥EF,且点D在AB的右侧,则∠CBD的度数为 . 15. 如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则BE+EF的最小值为 .
15. 如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则BE+EF的最小值为 .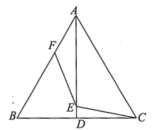
三、计算题(共8分)
-
16. 解下列不等式(组)(1)、;(2)、
四、作图题(共9分)
-
17. 如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:

( 1 )将△ABC向右平移5个单位长度,画出平移后的△A1B1C1 ;
( 2 )画出△ABC关于x轴对称的△A2B2C2 ;
( 3 )将△ABC绕原点O 旋转180°,画出旋转后的△A3B3C3 ;
五、解答题(共5题,共38分)
-
18. 图,△ABC 是边长为 2 的等边三角形,将△ABC 沿直线 BC 平移到△DCE 的位置,连接 BD,
 (1)、△ABC 平移的距离为;(2)、求 BD 的长.19. 已知,如图,在△ABC中,AB=AC,∠BAC=120°,AP⊥BC,垂足为D,且AP=AB.
(1)、△ABC 平移的距离为;(2)、求 BD 的长.19. 已知,如图,在△ABC中,AB=AC,∠BAC=120°,AP⊥BC,垂足为D,且AP=AB. (1)、求证:△ABP是等边三角形;(2)、若E是边AB上一点,∠EPF=60°,PF交AC于点F,试判断BE与AF的数量关系,并说明理由.20. 四边形ABCD中, , AB=13,BC=5,AC=AD=12,
(1)、求证:△ABP是等边三角形;(2)、若E是边AB上一点,∠EPF=60°,PF交AC于点F,试判断BE与AF的数量关系,并说明理由.20. 四边形ABCD中, , AB=13,BC=5,AC=AD=12, (1)、求∠ACB的度数.(2)、求CD的长,21. 某商家欲购进甲、乙两种商品共180件,其进价和售价如表:
(1)、求∠ACB的度数.(2)、求CD的长,21. 某商家欲购进甲、乙两种商品共180件,其进价和售价如表:甲
乙
售价(元/件)
14
35
进价(元/件)
20
43
(1)、若商家计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?(2)、若商家计划投入资金少于5040元,且销售完这批商品后获利不少于1314元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.22. 【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.如图,点是内的一点,将绕点逆时针旋转60°到 , 则可以构造出等边 , 得 , , 所以的值转化为的值,当 , , , 四点共线时,线段的长为所求的最小值,即点为的“费马点”.
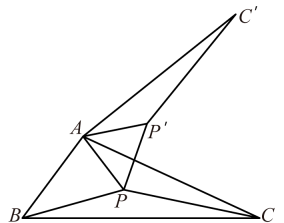 (1)、【拓展应用】
(1)、【拓展应用】如图1,点是等边内的一点,连接 , , , 将绕点逆时针旋转60°得到.
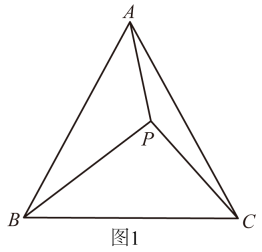
①若 , 则点与点之间的距离是 ▲ ;
②当 , , 时,求的大小;
(2)、如图2,点是内的一点,且 , , , 求的最小值.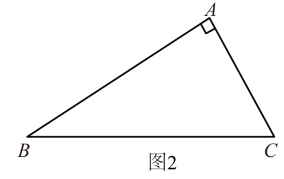
-
-