贵州省遵义市名校联考2022-2023学年七年级下学期4月月考数学试题

试卷更新日期：2023-04-12 类型：月考试卷

进入出卷网下载

一、选择题(本大题共12小题，每小题3分，共36分，每个题目只有唯一一个选项符合题意，请把正确答案填涂在答题卡相应位置．)

1. “水是生命之源，滋润着世间万物"国家节水标志由水滴，手掌和地球变形而成．寓意：像对待掌上明珠一样，珍惜每一滴水！以下通过平移左侧的节水标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 我国自主研发的北斗系统技术世界领先，2020年6月23日在西昌卫星发射中心成功发射最后一颗北斗三号组网卫星，该卫星发射升空的速度约为7100米/秒．将7100用科学记数法表示为（）

A、7.1×10³ B、0.71×10⁴ C、71×10² D、7100

查看试题解析
3. 如图，直线AB、CD相交于点O，OE⊥CD，垂足为点O．若∠BOE=50°，则∠AOC= （）

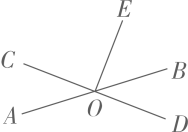A、140° B、50° C、60° D、40°

查看试题解析
4. 下列各数中，大于6且小于7的是（）

A、 $\sqrt{26}$ B、 $\sqrt{32}$ C、 $\sqrt{45}$ D、 $\sqrt{52}$

查看试题解析
5. 下列等式正确的是（）

A、 $\sqrt{\frac{9}{16}} = \pm \frac{3}{4}$ B、 $\sqrt{1 \frac{1}{9}} = 1 \frac{1}{3}$ C、 $^{3} \sqrt{- 9}$ =-3 D、 $\sqrt{(- \frac{1}{3})^{2}} = \frac{1}{3}$

查看试题解析
6. 已知a，b满足(a-1)²+ $\sqrt{b + 2}$ =0，则a+b的值是（）

A、-2 B、2 C、-1 D、0

查看试题解析
7. 下列选项中，能说明命题“两个锐角的和是锐角”是一个假命题的反例是（）

A、∠A=40°，∠B=50° B、∠A=30°，∠B=90° C、∠A=20°，∠B=60 D、∠A=50°，∠B=100°

查看试题解析
8. 如图，已知数轴上A，B两点表示的数分别是a，b，则计算|b|-|a|正确的是（）

A、a+b B、a-b C、b-a D、-a-b

查看试题解析
9. 如图，下面推理过程正确的是（）

A、因为∠B=∠BCD，所以AB∥CD B、因为∠1=∠2．所以AB∥CD C、因为∠BAD+∠B=180°，所以AD∥BC D、因为∠1=∠B，所以AD∥BC

查看试题解析
10. 如图，在宽为20米、长为30米的矩形地面上修筑宽均为2米的道路(图中阴影部分)，余下部分种植草坪．则草坪的面积为（）平方米．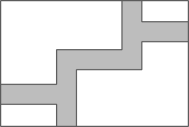

A、500 B、504 C、530 D、534

查看试题解析
11. 如图，把一张长方形的纸按图那样折叠后，B，C两点落在B₁ ， C₁处，若∠AEB₁=70，则∠BEF=（）

A、70° B、60° C、65° D、55°

查看试题解析
12. 小红在“趣味数学”社团活动中探究了直线交点个数的问题．现有7条不同的直线ln(n=1，2，3，4，5，6，7)，其中l₁、l₂互相平行，l₃、l₄、I₅三条直线交于一点，则他探究这7条直线的交点个数最多是（）

A、17个 B、18个 C、19个 D、21个

查看试题解析

二、填空题(本大题共4小题，每小题4分，共16分，请把正确答案填写在答题卡相应位置上．)

13. 实数3.141， $^{3} \sqrt{- 27}$ ， π， $- \sqrt{2}$ ， $\frac{22}{7}$ ， 0.2，0.1010010001……中无理数有个 (填个数)．

查看试题解析
14. 如图，∠1=60°，∠2=120°，∠3=70°，则∠4的度数是

查看试题解析
15. 比较大小： $\frac{\sqrt{5} + 1}{2}$ $\frac{3}{2}$

查看试题解析
16. 如图，已知AB∥EF，∠C=90°，则α、β与γ的关系是.

查看试题解析

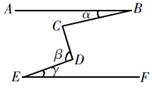
三、解答题(本大题共9小题，共98分，解答要写出必要的文字说明、证明过程或

17. 计算：

(1)、 $\sqrt{25} -^{3} \sqrt{27} + (- 3)^{^{2}}$

(2)、 $(3 \sqrt{3} - 2 \sqrt{2}) - 2 (\sqrt{3} - \sqrt{2})$

查看试题解析
18. 求下列各式中的x的值．

(1)、 (3x+2)²=16；

(2)、 $\frac{1}{2}$ (2x-1)³=-4．

查看试题解析
19. 如图，点O是直线AB上一点，射线OC、OD、OE在直线AB的同一侧，且OC平分∠AOE，OD⊥OC．

(1)、如果∠COE=40°，求∠AOD的度数．

(2)、如果∠AOE+30°=∠BOE，求∠BOD的度数．

查看试题解析
20. (10分)如图，在边长为1个单位长度的小正方形组成的网格中．

(1)、把△ABC进行平移得到△A'B'C'，使点B与B'对应，请在网格中画出；

(2)、线段AA'与线段CC'的数量关系和位置关系是

(3)、平移过程中，线段BC扫过的面积是

查看试题解析
21. 列方程解应用题．小丽给了小明一张长方形的纸片，告诉他，纸片的长宽之比为3：2，纸片面积为294 cm² ．

(1)、请你帮小明求出纸片的周长．

(2)、小明想利用这张纸片裁出一张面积为157cm²的完整圆形纸片，他能够裁出想要的圆形纸片吗？请说明理由．(π取3.14)

查看试题解析
22. 我们知道 $\sqrt{2}$ ≈1.414，于是我们说：“ $\sqrt{2}$ 的整数部分为1，小数部分则可记为 $\sqrt{2}$ -1”．则：

(1)、 $\sqrt{2}$ +1的整数部分是，小数部分可以表示为

(2)、已知 $\sqrt{3}$ +2的小数部分是a，7- $\sqrt{3}$ 的小数部分为b．那a+b=

(3)、已知 $\sqrt{11}$ 的整数部分为x， $\sqrt{11}$ 的小数部分为y，求(y- $\sqrt{11}$ )^x-1的平方根．

查看试题解析
23. 如图所示的是一个潜望镜模型示意图，AB，CD代表镜子摆放的位置，并且AB与CD平行，光线经过镜子反射时，满足∠1=∠2，∠3=∠4．
证明离开潜望镜的光线MN平行于进入潜望镜的光线EF．

请补全下述证明过程：

∵AB∥CD，

∴∠2=_▲_

∵∠1=∠2，∠3=∠4，

∴_▲_

∵∠1+∠2+∠5=180°，∠3+∠4+_▲_=180°，

∴∠5=_▲_

∴MN∥EF(本空填依据： )

查看试题解析
24. 如图，BD平分∠ABC，F在AB上，G在AC上，FC与BD相交于点H，∠3+∠4=180°，试说明∠1=∠2．

查看试题解析
25. 数学中，常对同一个量用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．

(1)、[探究一]

方法1：如图1，在边长为a的正方形纸片上剪去一个边长为b(b<a)的正方形，你能表示图中阴影部分的面积吗？阴影部分的面积是.

方法2：如图2．也可以把阴影部分沿着虚线AB剪开，分成两个梯形，计算阴影部分的面积是.

用两种不同的方法计算同一个阴影部分的面积，可以得到等式.

(2)、 [探究二]
如图3，一条直线上有n个点，请你数一数共有多少条线段呢？
方法1：一路往右数，不回头数．
以A₁为端点的线段有A₁A₂、A₁A₃、A₁A₄、A₁A₅、……A₁A_n ，共有(n-1)条；
以A₂为端点的线段有A₂A₃、A₂A₄、A₂A₅、……A₂A_n ，共有(n-2)条；
以A₃为端点的线段有A₃A₄、A₃A₅、……A₃A_n ．共有(n-3)条；
以A_n-1为端点的线段有A_n-1A_n ，共有1条；图中线段的总条数可用加法算式表示为.
方法2：每一个点都能和除它以外的(n-1)个点形成线段，共有n个点，共可形成n(n-1)条线段，但所有线段都数了两遍，所以线段的总条数是.
用两种不同的方法数线段，可以得到等式.

(3)、 [类比探究]如图，AC⊥BC，AC=3cm，BC=4cm，AB=5cm，点D为AB边的动点，求线段CD的最小值．

(4)、 [探究应用]计算：99²-98²+97²-96²+95²-94²+……+3²-2²+1² ．

查看试题解析

贵州省遵义市名校联考2022-2023学年七年级下学期4月月考数学试题

一、选择题(本大题共12小题， 每小题3分，共36分，每个题目只有唯一一个选项符合题意，请把正确答案填涂在答题卡相应位置．)

二、填空题(本大题共4小题，每小题4分，共16分，请把正确答案填写在答题卡相应位置上．)

三、解答题(本大题共9小题，共98分，解答要写出必要的文字说明、证明过程或

一、选择题(本大题共12小题，每小题3分，共36分，每个题目只有唯一一个选项符合题意，请把正确答案填涂在答题卡相应位置．)