辽宁省鞍山市2023届高三下学期数学第一次模拟联考试卷
试卷更新日期:2023-04-12 类型:高考模拟
一、单选题
-
1. 若 , 则( )A、 B、 C、1 D、22. 设全集 ,集合 ,则 ( )A、 B、 C、 D、3. 数学家也有许多美丽的错误,如法国数学家费马于1640年提出了 (n=0,1,2,…)是质数的猜想,直到1732年才被善于计算的大数学家欧拉算出 , 不是质数.现设 , 表示数列的前项和,若 , 则( )A、5 B、6 C、7 D、84. 已知平面向量与的夹角为 , , , 则的值为( )A、 B、2 C、4 D、5. 已知 , 则( )A、 B、 C、 D、6. 为了支援山区教育,现在安排5名大学生到3个学校进行支教活动,每个学校至少安排1人,其中甲校至少要安排2名大学生,则不同的安排方法共有( )种A、50 B、60 C、80 D、1007. 已知圆锥的母线长为2,侧面展开图扇形的面积为 ,那么该圆锥的体积是( )A、 B、 C、 D、8. 函数是定义在R上的偶函数,且 , 若 , , 则( )A、4 B、2 C、1 D、0
二、多选题
-
9. 为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入调查数据整理得到如下频率分布直方图(如图):

根据此频率分布直方图,下面结论中正确的是( )
A、该地农户家庭年收入低于4.5万元的农户比率估计为6% B、该地农户家庭年收入的中位数约为7.5万元 C、估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间 D、估计该地农户家庭年收入的平均值不超过6.5万元10. 已知函数的最小正周期为 , 且的图象过点 , 则下列结论中正确的是( )A、的最大值为 B、的图象一条对称轴为 C、在上单调递减 D、把的图象向左平移个单位长度,得到函数的图象11. 已知分别是双曲线的左、右焦点,点是该双曲线的一条渐近线上的一点,并且以线段为直径的圆经过点 , 则( )A、双曲线的渐近线方程为 B、以线段为直径的圆的方程为 C、点的横坐标为或 D、的面积为12. 如图所示,从一个半径为 (单位:m)的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥 ,则以下说法正确的是( )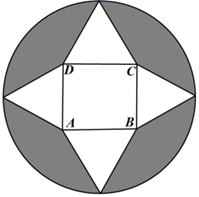 A、四棱锥 的体积是 B、四棱锥 的外接球的表面积是 C、异面直线 与 所成角的大小为 D、二面角 所成角的余弦值为
A、四棱锥 的体积是 B、四棱锥 的外接球的表面积是 C、异面直线 与 所成角的大小为 D、二面角 所成角的余弦值为三、填空题
-
13. 在展开式中,常数项是.14. 若函数的图像在点处的切线方程为 , 则实数 .15. 若正实数 ,满足 ,则 的最小值为.16. 已知椭圆C:的左、右顶点分别为 , ,且以线段 , 为直径的圆与直线相切,则椭圆C的离心率为.
四、解答题
-
17. 设数列的前n项和为 , 且满足 , .(1)、求数列的通项公式:(2)、若 , 求数列的前n项和 .18. 在ABC中,角A,B,C所对的边分别为a,b,c, , , 延长BC至D,使 , 的面积为 .(1)、求AB的长;(2)、求外接圆的面积.19. 甲、乙、丙三人,为了研究某地区高中男生的体重(单位:)与身高(单位:)是否存在较好的线性关系,他们随机调查了6名高中男生身高和体重的数据,得到如下表格:
身高/
体重/

根据表中数据计算得到关于的线性回归方程对应的直线的斜率为.
(1)、求关于的线性回归方程;(2)、从该地区大量高中男生中随机抽出位男生,他们身高(单位:)的数据绘制成如图的茎叶图.①估计体重超过的频率 ,
②视频率为概率,从该地区大量高中男生中随机选出人,记这人中体重超过的人数为 , 求的分布列及其数学期望(用(1)中的回归方程估测这位男生的体重).
20. 如图,在四棱锥中,底面ABCD为直角梯形, , , , 为等边三角形,且面底面ABCD. (1)、若M为BC中点,求证:;(2)、求面PAD与面PBC所成二面角的余弦值.
(1)、若M为BC中点,求证:;(2)、求面PAD与面PBC所成二面角的余弦值.