江苏省2023年普通高中数学学业水平合格性考试试卷

试卷更新日期：2023-04-12 类型：水平会考

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 2 ， 0 ， 2} ， B = {0 ， 2 ， 4}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 2}$ B、 ${- 2 ， 2 ， 4}$ C、 ${- 2 ， 0 ， 2}$ D、 ${- 2 ， 0 ， 2 ， 4}$

查看试题解析
2. 已知 $a > b$ ，则（）

A、 $a + 3 > b + 3$ B、 $3 - a > 3 - b$ C、 $\frac{3}{a} > \frac{3}{b}$ D、 $a^{2} > b^{2}$

查看试题解析
3. 已知 $z = 3 - i$ ，则 $| z | =$ （）

A、3 B、4 C、 $\sqrt{10}$ D、10

查看试题解析
4. 已知五个数 $2 ， a ， 6 ， 5 ， 3$ 的平均数为4，则 $a =$ （）

A、3 B、4 C、5 D、6

查看试题解析
5. 命题“ $\forall x \in R$ ， $x^{2} + x + 1 > 0$ ”的否定为（）

A、 $\forall x \in R$ ， $x^{2} + x + 1 \leq 0$ B、 $\exists x \in R$ ， $x^{2} + x + 1 \leq 0$ C、 $\exists x \in R$ ， $x^{2} + x + 1 < 0$ D、 $\exists x \in R$ ， $x^{2} + x + 1 > 0$

查看试题解析
6. 已知角 $α$ 的终边经过点 $P (2 ， - 1)$ ，则 $\sin α =$ （）

A、 $\frac{\sqrt{5}}{5}$ B、 $- \frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $- \frac{2 \sqrt{5}}{5}$

查看试题解析
7. 函数 $f (x) = \sqrt{\frac{1}{x - 1}}$ 的定义域为（）

A、 $(- \infty ， 1]$ B、 $(- \infty ， 1)$ C、 $[1 ， + \infty)$ D、 $(1 ， + \infty)$

查看试题解析
8. 要得到函数 $y = 2 s i n (x + \frac{π}{3})$ 的图象．只需将函数 $y = 2 s i n x$ 的图象（）

A、向左平移 $\frac{π}{3}$ 个单位 B、向右平移 $\frac{π}{3}$ 个单位 C、向左平移 $\frac{π}{6}$ 个单位 D、向右平移 $\frac{π}{6}$ 个单位

查看试题解析
9. 党的二十大报告指出：“全面提高人才自主培养质量，着力造就拔尖创新人才，聚天下英才而用之.”某区域教育部门为提高学生的创新能力，组织了200名学生参与研究性学习，每人仅参加1个课题组，参加各课题组的人数占比的扇形统计图如图所示，则参加数学类的人数比参加理化类的人数多（）

A、16 B、30 C、32 D、62

查看试题解析
10. 从甲､乙､丙､丁4名同学中任选3名同学参加环保宣传志愿服务，则甲被选中的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
11. 已知 $a = l o g_{3} \frac{1}{2} ， b = l o g_{3} 2 ， c = l o g_{2} 3$ ，则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < b < a$

查看试题解析
12. 已知直线 $l$ $∥$ 平面 $α$ ，直线 $m \subset$ 平面 $α$ ，则 $l$ 与 $m$ 不可能（）

A、平行 B、相交 C、异面 D、垂直

查看试题解析
13. 已知函数 $f (x) = x^{α}$ 是偶函数，且在区间 $(0 ， + ∞)$ 上单调递增，则下列实数可作为 $α$ 值的是（）

A、-2 B、 $\frac{1}{2}$ C、2 D、3

查看试题解析
14. 已知 $t a n α = - 3$ ，则 $\frac{s i n α + 2 c o s α}{s i n α - c o s α} =$ （）

A、 $\frac{5}{2}$ B、 $\frac{1}{4}$ C、 $- \frac{5}{4}$ D、 $- \frac{7}{2}$

查看试题解析
15. 对于两个非空实数集合 $A$ 和 $B$ ，我们把集合 ${x ∣ x = a + b ， a \in A ， b \in B}$ 记作 $A * B$ .若集合 $A = {0 ， 1} ， B = {0 ， - 1}$ ，则 $A * B$ 中元素的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
16. 已知函数 $f (x)$ 为奇函数，且当 $x > 0$ 时， $f (x) = l o g_{3} (2 x + 1)$ ，则 $f (- 1) =$ （）

A、-1 B、0 C、1 D、2

查看试题解析
17. 甲､乙两人独立地破译某个密码，如果每人译出密码得概率均为0.3，则密码被破译的概率为（）

A、0.09 B、0.42 C、0.51 D、0.6

查看试题解析
18. 甲､乙､丙､丁4名学生参加数学竞赛，在成绩公布前，4人作出如下预测：甲说：乙第一；乙说：丁第一；丙说：我不是第一；丁说：乙第二.公布的成绩表明，4名学生的成绩互不相同，并且有且只有1名学生预测错误，则预测错误的学生是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
19. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，直线 $B D_{1}$ 与平面 $A B C D$ 所成角的正切值为（）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{3}$

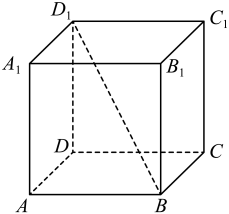查看试题解析
20. 在一次实验中，某小组测得一组数据 $(x_{i} ， y_{i}) (i = 1 ， 2 ， ⋯ ， 11)$ ，并由实验数据得到下面的散点图.由此散点图，在区间 $[- 2 ， 3]$ 上，下列四个函数模型 $(a ， b$ 为待定系数）中，最能反映 $x ， y$ 函数关系的是（）

A、 $y = a + b x$ B、 $y = a + b^{x}$ C、 $y = a + l o g_{b} x$ D、 $y = a + \frac{b}{x}$

查看试题解析
21. 在 $△ A B C$ 中，已知 $c o s 2 A = - \frac{3}{5}$ ，则 $s i n A =$ （）

A、 $- \frac{2 \sqrt{5}}{5}$ B、 $\frac{4}{5}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
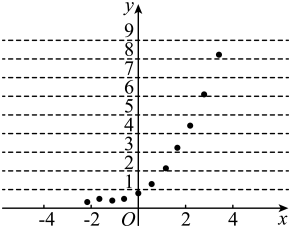22. 已知 $△ A B C$ 是边长为2的等边三角形， $D ， E ， F$ 分别是边 $A B ， B C ， C A$ 的中点，则（）

A、 $\vec{A B} + \vec{A C} = \vec{A E}$ B、 $\vec{A B} - \vec{A C} = \vec{B C}$ C、 $\vec{E F} = \frac{1}{2} \vec{A B}$ D、 $\vec{D E} \cdot \vec{D F} = \frac{1}{2}$

查看试题解析
23. 在空间，到一个三角形的三个顶点距离相等的点的集合表示的图形是（）

A、一个点 B、一条直线 C、一个平面 D、一个球面

查看试题解析
24. 已知向量 $\vec{a} = (2 ， 0) ， \vec{b} = (1 ， \sqrt{3}) ， (\vec{a} + k \vec{b}) ⊥ (k \vec{a} - \vec{b})$ ，则实数 $k =$ （）

A、-1 B、0 C、1 D、-1或1

查看试题解析
25. 两游艇自某地同时出发，一艇以 $10 k m / h$ 的速度向正北方向行驶，另一艇以 $8 k m / h$ 的速度向北偏东 $θ$ （ $0 ° < θ < 90 °$ ）角的方向行驶.若经过 $30 m i n$ ，两艇相距 $\sqrt{21}$ $k m$ ，则 $θ$ $=$ （）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
26. 2023年2月6日，土耳其发生强烈地震，造成重大人员伤亡和财产损失，江苏救援队伍紧急赴当地开展救报行动.尽管日前人类还无法准确预报地震，但科学家通过研究，已经对地震有所了解，例如，地震时释放的能量E（单位：焦耳）与地震里氏震级M之间的关系为 $l g E = 4.8 + 1.5 M$ .里氏8.0级地震所释放出来的能量是里氏6.0级地震所释放出来的能量的（）

A、6倍 B、 $1 0^{2}$ 倍 C、 $1 0^{3}$ 倍 D、 $1 0^{6}$ 倍

查看试题解析
27. 若圆柱的上､下底面的圆周都在一个半径为2的球面上，则该圆柱侧面积的最大值为（）

A、 $4 π$ B、 $8 π$ C、 $12 π$ D、 $16 π$

查看试题解析
28. 若函数 $f (x) = {\begin{array}{l} x^{2} - 2 x - m + 1 ， x < 3 \\ m s i n x + 1 ， x \geq 3 \end{array}$ 的值域为 $[- 2 ， + \infty)$ ，则实数 $m$ 的可能值共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、解答题

29. 如图，三棱锥 $P - A B C$ 的底面 $A B C$ 和侧面 $P B C$ 都是边长为2的等边三角形， $M ， N$ 分别是 $A B ， B C$ 的中点， $P N ⊥ A N$ .

(1)、证明： $M N$ $/ /$ 平面 $P A C$ ；

(2)、求三棱锥 $P - A B C$ 的体积.

查看试题解析
30. 已知函数 $f (x) = s i n x$ .

(1)、求函数 $y = f (2 x + \frac{π}{3})$ 的最小正周期；

(2)、若 $[f (x)]^{2} + m | f (x) - \frac{1}{2} | \geq \frac{1}{8}$ ，求实数 $m$ 的取值范围.

查看试题解析