浙江省绍兴市柯桥区联盟校2022-2023学年九年级下学期3月学科课堂作业数学试题(一)
试卷更新日期:2023-04-11 类型:月考试卷
一、单选题
-
1. 和点A(5,-4)关于x轴对称的点的坐标是( )A、(-5,-4) B、(5,4) C、(5,-4) D、(-5,4)2. 长江是我国第一大河,它的全长约为6300千米,6300这个数用科学记数法表示为( ).A、 B、 C、 D、3. 下列四个立体图形中,从正面看到的图形与其他三个不同的是( )A、
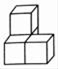 B、
B、 C、
C、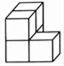 D、
D、 4. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )A、 B、 C、 D、5. 若点 , , 在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、6. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )
4. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )A、 B、 C、 D、5. 若点 , , 在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、6. 矩形相邻的两边长分别为25和 , 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则的值为( )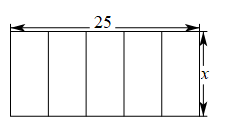 A、5 B、 C、 D、107. 在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径和∠MND的度数分别为( )
A、5 B、 C、 D、107. 在等腰直角三角形ABC中,AB=AC=4,点O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,则⊙O的半径和∠MND的度数分别为( ) A、2,22.5° B、3,30° C、3,22.5° D、2,30°8. 如图所示,以AD为直径的半圆O经过 的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点, 的长为 ,则图中阴影部分的面积为( ).
A、2,22.5° B、3,30° C、3,22.5° D、2,30°8. 如图所示,以AD为直径的半圆O经过 的斜边AB的两个端点,交直角边AC于点E,点B、E是半圆弧的三等分点, 的长为 ,则图中阴影部分的面积为( ). A、 B、 C、 D、9. 若二次函数 的图象如图所示,则坐标原点可能是( )
A、 B、 C、 D、9. 若二次函数 的图象如图所示,则坐标原点可能是( ) A、点 B、点 C、点 D、点10. 矩形纸片中, , 将纸片对折,使顶点A与顶点C重合,得折痕 , 将纸片展开铺平后再进行折叠,使顶点B与顶点D重合,得折痕 , 展开铺平后如图所示.若折痕与较小的夹角记为 , 则的值是( )
A、点 B、点 C、点 D、点10. 矩形纸片中, , 将纸片对折,使顶点A与顶点C重合,得折痕 , 将纸片展开铺平后再进行折叠,使顶点B与顶点D重合,得折痕 , 展开铺平后如图所示.若折痕与较小的夹角记为 , 则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若是方程的一个解,则.12. 某商场开展购物抽奖活动,抽奖箱内有标号分别为1、2、3、4、5、6、7、8、9、10十个质地、大小相同的小球,顾客从中任意摸出一个球,摸出的球的标号是3的倍数就得奖,顾客得奖概率是.13. 小明在手工制作课上,用面积为 ,半径为 的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为 .14. 如图,矩形 的顶点 在双曲线 上, , 两点分别在 轴, 轴的正半轴上,将矩形 绕点 顺时针旋转90°,得到矩形 ,边 , 分别交此双曲线于 , 两点,若 , 的面积为1,则 .
 15. 如图,点B为线段AQ上的动点,AQ=8 ,以AB为边作正△ABC,以BC为底边作等腰三角形PCB,则PQ的最小值为 .
15. 如图,点B为线段AQ上的动点,AQ=8 ,以AB为边作正△ABC,以BC为底边作等腰三角形PCB,则PQ的最小值为 .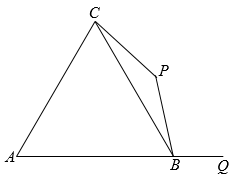 16. 汉代数学家赵爽为了证明勾股定理,构造了一副“弦图”,后人称其为“赵爽弦图”.如图,大正方形由四个全等的直角三角形和一个小正方形组成,若 , 的面积为3,则.
16. 汉代数学家赵爽为了证明勾股定理,构造了一副“弦图”,后人称其为“赵爽弦图”.如图,大正方形由四个全等的直角三角形和一个小正方形组成,若 , 的面积为3,则.
三、解答题
-
17.(1)、计算:.(2)、解方程:18. 如图,在方格纸中,每个小正方形的边长都是1,点A,B,P都在格点上,请按要求画出图形,使点P在所画图形的内部(不包括边界上).
 (1)、请在图1中作出一个▱ABCD,点C和点D都在格点上;(2)、请在图2中画一个四边形ABEF,使得EFAB,且∠A是钝角,点E和点F都在格点上.19. “芡实糕”是一种南浔的传统特色糕点,某糕点店为了了解该地居民对去年销量较好的芝麻味(A)、紫薯味(B)、红糖味(C)、桂花味(D)四种不同口味的喜爱情况,对该地居民进行了抽样调查,并将调查情况绘制成如下两幅不完整的统计图.
(1)、请在图1中作出一个▱ABCD,点C和点D都在格点上;(2)、请在图2中画一个四边形ABEF,使得EFAB,且∠A是钝角,点E和点F都在格点上.19. “芡实糕”是一种南浔的传统特色糕点,某糕点店为了了解该地居民对去年销量较好的芝麻味(A)、紫薯味(B)、红糖味(C)、桂花味(D)四种不同口味的喜爱情况,对该地居民进行了抽样调查,并将调查情况绘制成如下两幅不完整的统计图.请根据以上信息回答:
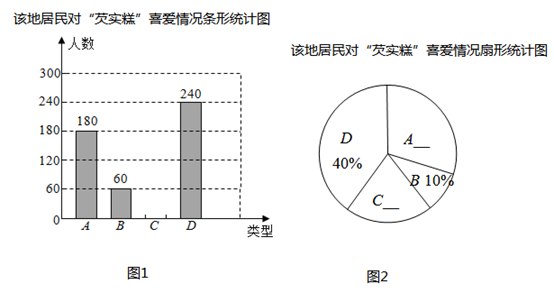 (1)、本次参加抽样调查的居民人数是多少人;(2)、请直接将两幅统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(3)、若该地居民有36000人,请估计爱吃D口味“芡实糕”有多少人?20. 如图,已知二次函数y=x2+ax+a+1的图象经过点P(﹣2,3).
(1)、本次参加抽样调查的居民人数是多少人;(2)、请直接将两幅统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(3)、若该地居民有36000人,请估计爱吃D口味“芡实糕”有多少人?20. 如图,已知二次函数y=x2+ax+a+1的图象经过点P(﹣2,3). (1)、求a的值和图象的顶点坐标.(2)、点Q(m,n)在该二次函数图象上.
(1)、求a的值和图象的顶点坐标.(2)、点Q(m,n)在该二次函数图象上.①当m=2时,求n的值.
②当m≤x≤m+3时,该二次函数有最小值11,请根据图象直接写出m的值.
21. 如图1,是一电动门,当它水平下落时,可以抽象成如图2所示的矩形 , 其中 , , 此时它与出入口等宽,与地面的距离;当它抬起时,变为平行四边形 , 如图3所示,此时,与水平方向的夹角为.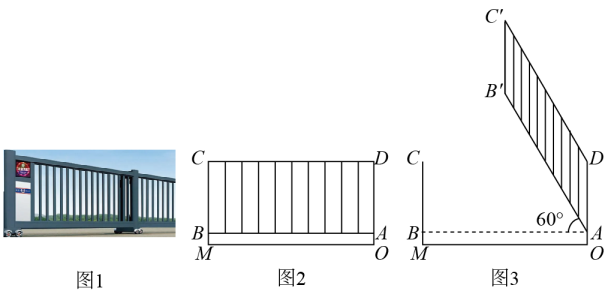 (1)、求点到地面的距离;(2)、在电动门抬起的过程中,求点所经过的路径长;(3)、一辆高 , 宽的汽车从该入口进入时,汽车需要与保持的安全距离,此时,汽车能否安全通过,若能,请通过计算说明;若不能,说明理由.(参考数据: , , 所有结果精确到22. 瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
(1)、求点到地面的距离;(2)、在电动门抬起的过程中,求点所经过的路径长;(3)、一辆高 , 宽的汽车从该入口进入时,汽车需要与保持的安全距离,此时,汽车能否安全通过,若能,请通过计算说明;若不能,说明理由.(参考数据: , , 所有结果精确到22. 瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:(元)
19
20
21
30
(件)
62
60
58
40
(1)、根据表中数据的规律,分别写出每日销售量y(件),每日的利润w(元)关于销售单价x(元)之间的函数表达式.(利润=(销售单价-成本单价)×销售件数).(2)、当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?(3)、根据物价局规定,这种纪念品的销售单价不得高于32元,如果公司要获得每日不低于350元的利润,那么制造这种纪念花灯每日的最低制造成本需要多少元?23. 如图: (1)、【证明体验】如图(1),在中, , 平分交于 , 点在上, , 连接 , 求证:.(2)、【思考探究】如图(2),在(1)的条件下,过点作交于点 , 交于点 , 若 , , 求的长.(3)、【拓展延伸】如图(3),在四边形中, , 且 , 若 , , 则.24. B,C是⊙O上的两个定点,A是圆上的动点, , , .
(1)、【证明体验】如图(1),在中, , 平分交于 , 点在上, , 连接 , 求证:.(2)、【思考探究】如图(2),在(1)的条件下,过点作交于点 , 交于点 , 若 , , 求的长.(3)、【拓展延伸】如图(3),在四边形中, , 且 , 若 , , 则.24. B,C是⊙O上的两个定点,A是圆上的动点, , , . (1)、如图1,如果是等边三角形,求证是⊙O的切线;(2)、如图2,如果 , , 分别交⊙O于E,F,研究五边形的性质;
(1)、如图1,如果是等边三角形,求证是⊙O的切线;(2)、如图2,如果 , , 分别交⊙O于E,F,研究五边形的性质;①探索、和的数量关系,并证明你的结论;
②如图3,若⊙O的半径为6, , 求边的长;
③若 , , 直接写出 , 的数量关系.