浙江省宁波七中教育集团2022-2023学年九年级下学期第三次月考数学试题
试卷更新日期:2023-04-11 类型:月考试卷
一、单选题
-
1. -3,4,0,这四个数中,无理数是( )A、-3 B、4 C、0 D、2. 根据实时统计数据,截至北京时间2022年3月24日24时,全球累计确诊新冠肺炎病例约47600万例,其中47600万例用科学记数法表示是( )例.A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4.
如图,摆放的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、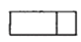 D、
D、 5. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差S2(单位:千克2)如下表所示:
5. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差S2(单位:千克2)如下表所示:甲
乙
丙
丁
x
24
24
23
20
S2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A、甲 B、乙 C、丙 D、丁6. 下列能说明命题“若 , 则”是假命题的反例是( )A、 , B、 , C、 , D、 ,7. 已知抛物线y=ax2+bx+c,经过A(4,9),B(12,9)两点,那么它的对称轴是( )A、直线x=7 B、直线x=8 C、直线x=9 D、无法确定8. 我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有 人, 辆车,则可列方程组为( )A、 B、 C、 D、9. 如图,正方形的面积为12,点E在边上,且 , 的平分线交于点F,点M,N分别是 , 的中点,则的长为( ) A、 B、 C、 D、10. 矩形 内放入两张边长分别为 和 的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为 ;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为 ;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为 .已知 , ,设 ,则下列值是常数的是( )
A、 B、 C、 D、10. 矩形 内放入两张边长分别为 和 的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为 ;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为 ;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为 .已知 , ,设 ,则下列值是常数的是( )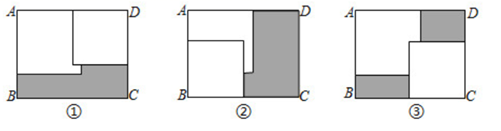 A、 B、 C、 D、a+b
A、 B、 C、 D、a+b二、填空题
-
11. 二次根式 中,x的取值范围是 .12. 分解因式:3a2﹣12= .13. 袋中装有除颜色外其余都相同的8个红球和6个白球.从袋中任意摸出一个球,则摸出的球是白球的概率为.14. 已知一个圆锥的底面半径为 ,母线长为 ,则这个圆锥的侧面积为 .15. 定义:以直角三角形的重心为圆心,且与该直角三角形的一边相切的圆叫做这个直角三角形的重切圆.斜边为10,重切圆半径为2的直角三角形的面积是.16. 如图,平面直角坐标系中,O为原点,点A,B分别在y轴、x轴的正半轴上,的两条外角平分线交于点 , 且点在反比例函数的图象上, , 的延长线分别交轴、轴于点 , , 连结.的面积为9,则的值是;当点A的坐标为时,则点的坐标是.

三、解答题
-
17.(1)、计算:(2)、解方程:18. 如图是4×4的正方形网格,△ABC的三个顶点均在格点上
 (1)、将△ABC绕点A顺时针方向旋转90°得到△AB1C1 , 在图①中作出△AB1C1;(2)、在图②中作格点△A2B2C2 , 使△A2B2C2∽△ABC,且周长比为.19. 如图,正比例函数的图象与反比例函数的图象都经过A(-3,a).
(1)、将△ABC绕点A顺时针方向旋转90°得到△AB1C1 , 在图①中作出△AB1C1;(2)、在图②中作格点△A2B2C2 , 使△A2B2C2∽△ABC,且周长比为.19. 如图,正比例函数的图象与反比例函数的图象都经过A(-3,a). (1)、求点的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到x轴的距离小于2,请根据图象直接写出m的取值范围.20. 某校为了促进学生的个性发展,计划开设四类拓展性课程,包括艺术体育类、自然科学类、人文社科类及其他类(每人限选一项,要求人人都要参加).为了解学生喜爱哪种课程,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图.
(1)、求点的坐标和反比例函数表达式.(2)、若点在该反比例函数图象上,且它到x轴的距离小于2,请根据图象直接写出m的取值范围.20. 某校为了促进学生的个性发展,计划开设四类拓展性课程,包括艺术体育类、自然科学类、人文社科类及其他类(每人限选一项,要求人人都要参加).为了解学生喜爱哪种课程,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图.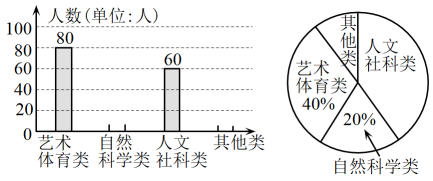
请根据图中的信息回答下列问题:
(1)、此次抽样调查的样本容量是人;(2)、求人文社科类在扇形统计图中所占圆心角的度数;(3)、请将条形统计图补充完整;(4)、若该校有1500名学生,请估计喜欢艺术体育类拓展课的学生人数.21. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量广场 两点之间的距离.如图所示,小星站在广场的 处遥控无人机,无人机在 处距离地面的飞行高度是 ,此时从无人机测得广场 处的俯角为 ,他抬头仰视无人机时,仰角为 ,若小星的身高 (点 在同一平面内).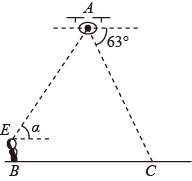 (1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).22. 某超市销售某种儿童玩具,每件进价为50元.根据市场调查发现:该玩具销售单价为100元时,每月的销售量为50件,而销售单价每降低1元,则每月可多售出5件.要求销售单价不得低于成本,且不高于110元.(1)、求该儿童玩具每月的销售量y(件)与销售单价x(元)之间的函数表达式;(2)、设超市每月销售这种玩具可获利W(元),当销售单价x为多少时W最大?W最大值是多少?23. 如图1,在中, , D是的中点,点E在线段上,连结 , 作交直线于点F,连结.
(1)、求仰角 的正弦值;(2)、求 两点之间的距离(结果精确到 ).22. 某超市销售某种儿童玩具,每件进价为50元.根据市场调查发现:该玩具销售单价为100元时,每月的销售量为50件,而销售单价每降低1元,则每月可多售出5件.要求销售单价不得低于成本,且不高于110元.(1)、求该儿童玩具每月的销售量y(件)与销售单价x(元)之间的函数表达式;(2)、设超市每月销售这种玩具可获利W(元),当销售单价x为多少时W最大?W最大值是多少?23. 如图1,在中, , D是的中点,点E在线段上,连结 , 作交直线于点F,连结. (1)、【初步尝试】
(1)、【初步尝试】如图2,当 , 线段的长度是 , 线段的长度是.
(2)、【结论探究】如图1,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如下表所示,请帮小宁完成证明.
如图,延长至G,使 , 连结 , .
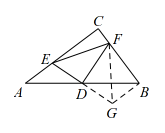 (3)、【拓展应用】
(3)、【拓展应用】如图3,当点E在线段的延长线上时,连结 , 作交直线于点F,连结.请补全图形,并求出当时,线段的长.
24. 如图,半圆中,直径 , 点为弧的中点,点在弧上,连结并延长交的延长线于点 , 连结交于点 , 连结.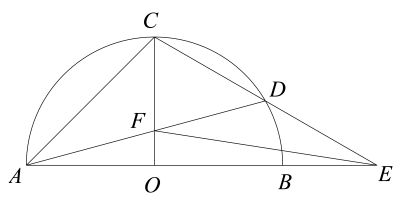 (1)、求证:.(2)、若点为中点,求的长.(3)、①面积与面积的差是定值吗?如果是,请求出该定值;若不是,请说明理由;
(1)、求证:.(2)、若点为中点,求的长.(3)、①面积与面积的差是定值吗?如果是,请求出该定值;若不是,请说明理由;②若 , 求的长.