浙江省杭州市西湖区十三中教育集团(总校)2022-2023学年九年级下学期3月月考数学试题
试卷更新日期:2023-04-11 类型:月考试卷
一、单选题
-
1. 计算的结果是( )A、 B、4 C、 D、62. 若 , 则括号内应填的代数式是( )A、 B、 C、 D、3. 某厂规定,工人完成定额20个零件,每天收入28元,如果超额生产一个零件,增加收入1.5元.一工人某天生产了26个零件,则该工人此天收入( )A、39元 B、38元 C、37元 D、36元4. 已知在中, , , , 那么( )A、 B、 C、 D、5. 若 , ,则( )A、 B、 C、 D、6. 在同一平面直角坐标系中,一次函数的图象过点 , 则该函数的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 7. 五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是()A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数8. 若三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、9. 如图,在圆内接四边形中, , 为直径,若四边形的面积是S,的长是x,则S与x之间的数关系式是( )
7. 五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是()A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数8. 若三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、9. 如图,在圆内接四边形中, , 为直径,若四边形的面积是S,的长是x,则S与x之间的数关系式是( ) A、 B、 C、 D、10. 已知二次函数(a为实数,且),对于满足的任意一个x的值,都有 , 则的最大值为( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二次函数(a为实数,且),对于满足的任意一个x的值,都有 , 则的最大值为( )A、 B、 C、 D、二、填空题
-
11. 若 , 则.12. 如图,点A,B,C在⊙O上, , , 则.
 13. 若 , , , 若 , , 则.14. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.15. 如图,中, , 为的角平分线,以点O为圆心,为半径作与边交于点D.若 , , 则.
13. 若 , , , 若 , , 则.14. 学校组织秋游,安排给九年级3辆车,小明和小慧都可以从这3辆车中任选一辆搭乘.则小明和小慧同车的概率为.15. 如图,中, , 为的角平分线,以点O为圆心,为半径作与边交于点D.若 , , 则. 16. 如图,在正方形中,点E,F分别在边 , 上,且 , 与 , 分别交于点M,N.
16. 如图,在正方形中,点E,F分别在边 , 上,且 , 与 , 分别交于点M,N.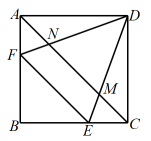 (1)、若 , , 则;(2)、设和的面积分别为和 , 若 , 则的.
(1)、若 , , 则;(2)、设和的面积分别为和 , 若 , 则的.三、解答题
-
17. 计算:(1)、(2)、解方程18. 某校图书管理员对一周内学生从图书馆借出各类图书的数量进行了统计,结果如图所示,请你根据统计图中的信息,解答下列问题:
 (1)、补全条形统计图和扇形统计图;(2)、求出学生最喜欢借阅漫画类图书所在扇形的圆心角的度数;(3)、该校计划购买新书共600本,若按扇形统计图中的百分比来确定每类图书的购买量,问应购买科普类图书多少本?19. 如图,在中,点是上的点,过点作交于点 , , 过作交于点.
(1)、补全条形统计图和扇形统计图;(2)、求出学生最喜欢借阅漫画类图书所在扇形的圆心角的度数;(3)、该校计划购买新书共600本,若按扇形统计图中的百分比来确定每类图书的购买量,问应购买科普类图书多少本?19. 如图,在中,点是上的点,过点作交于点 , , 过作交于点. (1)、若 , 求线段的长;(2)、若的面积为16,求的面积.20. 已知一次函数和反比例函数的图象交于P,Q两点.(1)、若一次函数图象过 , 且 , 求反比例函数的表达式;(2)、若P,Q关于原点成中心对称,当时, 总有 , 求n的取值范围.21. 如图,矩形中, , E是上一点,沿折叠,点A恰好落在线段的点F处,连接.
(1)、若 , 求线段的长;(2)、若的面积为16,求的面积.20. 已知一次函数和反比例函数的图象交于P,Q两点.(1)、若一次函数图象过 , 且 , 求反比例函数的表达式;(2)、若P,Q关于原点成中心对称,当时, 总有 , 求n的取值范围.21. 如图,矩形中, , E是上一点,沿折叠,点A恰好落在线段的点F处,连接. (1)、求证:;(2)、若 , 则;(3)、设 , , 求m与k满足的关系式.
(1)、求证:;(2)、若 , 则;(3)、设 , , 求m与k满足的关系式.
