湖北省荆州市2022-2023学年九年级下学期3月质检数学试题

试卷更新日期：2023-04-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{4}$ C、 $\sqrt{8}$ D、 $\sqrt{9}$

查看试题解析
2. 下列图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一个整数815550…0用科学记数法表示为8.1555×10¹⁰ ，则原数中“0”的个数为（）

A、4 B、6 C、7 D、10

查看试题解析
4. 将一副三角板和一张对边平行的纸条按如图摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是(　　)

A、15° B、22.5° C、30° D、45°

查看试题解析
5. 下列运算正确的是（）

A、 ${(x^{2})}^{3} = x^{5}$ B、 $\sqrt{6} \div \sqrt{2} = 3$ C、 $x \cdot x^{2} \cdot x^{3} = x^{5}$ D、 $(- x - y) (x - y) = y^{2} - x^{2}$

查看试题解析
6. 如图，是由四个大小相同的小正方体组成的几何体，这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
7. 如图所示， $⊙ O$ 的直径 $A B ⊥ C D$ 弦， $∠ 1 = 2 ∠ 2$ ，则 $t a n ∠ C D B =$ （）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $2$ D、 $1 + \sqrt{2}$

查看试题解析
8. 函数 $y = k x + b$ 的图象如图所示，则关于x的一元二次方程 $x^{2} + b x + k - 1 = 0$ 的根的情况是（）

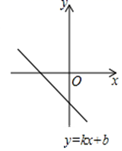A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
9. 野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海.现野鸭与大雁分别从南海和北海同时起飞，问经过多少天相遇？设野鸭与大雁经过x天相遇，根据题意，下面所列方程正确的是（）

A、 $\frac{x}{7} + \frac{x}{9} = 1$ B、 $\frac{x}{7} - \frac{x}{9} = 1$ C、 $(7 + 9) x = 1$ D、 $(9 - 7) x = 1$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点为 $M (2 ， 0)$ .下列结论：（1） $a c < 0$ ；（2） $2 a + b = 0$ ；（3）若关于x的方程 $a x^{2} + b x + c - t = 0$ 有两个不相等的实数根，则 $t > 0$ ；（4）若 $a {x_{1}}^{2} + b x_{1} = a {x_{2}}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ ，则 $x_{1} + x_{2} = 2$ .其中正确的结论有（）.

A、1个 B、2个 C、3 D、4个

查看试题解析

二、填空题

11. 分解因式： ${ab}^{2} - 4 a =$ .

查看试题解析
12. 已知关于x的分式方程 $\frac{m - 3}{x + 2} = 1$ 的解是负数，则m的取值范围是.

查看试题解析
13. 方程 $2 x^{2} - 4 x = 1$ 和方程 $2 x^{2} - x = 4$ 所有实数根之积为.

查看试题解析
14. 有一直径为2的圆形铁皮，要从中剪出一个最大圆心角为60°的扇形ABC，用此剪下的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径r=.

查看试题解析
15. 如图，在平面直角坐标系中，菱形 $O A B C$ 的顶点A在x轴上，顶点C在反比例函数的图象上，且 $∠ A O C = 60 ° .$ 若将该菱形向下平移2个单位后，顶点B恰好落在此反比例函数的图象上，则此反比例函数的表达式为.

查看试题解析
16. 如图，在平面直角坐标系中，长为3的线段 $C D$ （点D在点C右侧）在x轴上移动，点 $A (0 ， 2)$ 、 $B (0 ， 4)$ 是y轴上定点，连接 $A C 、 B D$ ，则 $A C + B D$ 的最小值为.

查看试题解析

三、解答题

17. 计算： $| - \sqrt{2} | - 2 \sin 45 ° + {(1 - \sqrt{3})}^{0} + \sqrt{2} \times \sqrt{8}$ .

查看试题解析
18. 先化简，再求值： $(\frac{a + 3}{a - 1} - \frac{1}{a - 1}) \div \frac{a^{2} + 4 a + 4}{a^{2} - a}$ ，其中a＝3．

查看试题解析
19. 为落实中小学生五项管理中的手机管理，某学校团委组织了“我与手机说再见”为主题的演讲比赛，根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图（其中A表示“一等奖”，B表示“二等奖”，C表示“三等奖”，D表示“优秀奖”）.
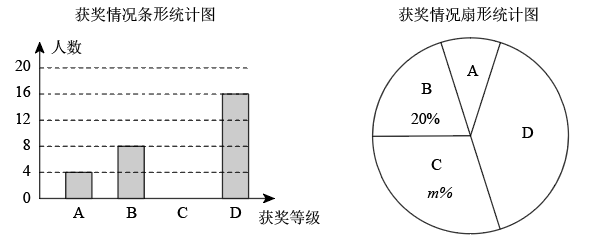
请你根据统计图中所提供的信息解答下列问题：

(1)、获奖总人数为人，m=；

(2)、请将条形统计图补充完整；

(3)、学校将从获得一等奖的4名同学（其中有一名男生，三名女生）中随机抽取两名参加全市的比赛，请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.

查看试题解析
20. 如图，正方形ABCD ，点E ， F分别在AD ， CD上，且DE＝CF ， AF与BE相交于点G ．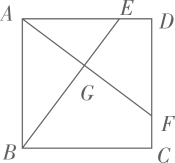

(1)、求证：BE＝AF；

(2)、若AB＝4，DE＝1，求AG的长．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{m}{x}$ 的图象相交于A，B两点，过点A作 $A D ⊥ x$ 轴于点D， $A O = 5$ ， $s i n ∠ A O D = \frac{4}{5}$ ， B点的坐标为 $(- 6 ， n)$ .

(1)、求一次函数和反比例函数的表达式；

(2)、求 $△ A O B$ 的面积；

(3)、P是y轴上一点，且 $△ A O P$ 是等腰三角形，请直接写出所有符合条件的P点坐标.

查看试题解析
22. 如图 $⊙ O$ 是 $△ A B C$ 的外接圆，点O在 $B C$ 上， $∠ B A C$ 的角平分线交 $⊙ O$ 于点D，连接 $B D$ ， $C D$ ，过点D作 $B C$ 的平行线与 $A C$ 的延长线相交于点P.

(1)、求证： $P D$ 是 $⊙ O$ 的切线；

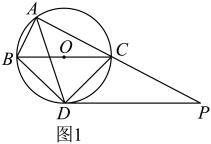(2)、若 $A B = 6$ ， $A C = 8$ ，求 $D C$ 与 $P C$ 的值.

查看试题解析

23. 某商店销售一种商品，经市场调查发现：该商品的周销售量 y (件) 是售价x（元/件）的一次函数，其售价、周销售量、周销售利润w（元）的三组对应值如下表：

售价x（元/件）	50	60	70
周销售量y（件）	80	60	40
周销售利润w（元）	800	1200	1200

注：周销售利润＝周销售量×（售价－进价）

(1)、求 y 关于 x 的函数解析式（不要求写出自变量的取值范围）；

(2)、求该商品的进价和周销售的最大利润；

(3)、由于某种原因，该商品进价提高了m元/件

(m > 0)

，物价部门规定该商品售价不得超过60元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系.若周销售最大利润是1080元，求m的值.

查看试题解析

24. 如图，已知抛物线 $C_{1}$ ： $y = \frac{1}{2} x^{2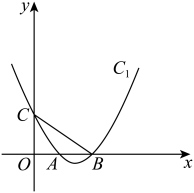} - 2 x + \frac{3}{2}$ 交x轴于点 $A ， B$ ，交y轴于点C.

(1)、直接写出点 $A ， B ， C$ 的坐标；

(2)、将直线 $B C$ 向下平移m个单位，使直线 $B C$ 与抛物线恰好只有一个公共点，求m的值；

(3)、在抛物线上存在点D，使 $t a n ∠ C B D = \frac{1}{2}$ ，求点D的坐标.

查看试题解析