湖北省黄石市大冶市还地桥镇教联体2023年九年级下学期第一学月数学试卷
试卷更新日期:2023-04-11 类型:月考试卷
一、单选题
-
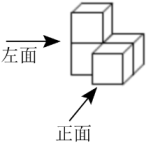
1. 在实数3.14,﹣π, ,﹣ 中,倒数最小的数是( )A、 B、 C、﹣π D、3.142. 下列图形:①国旗上的五角星,②有一个角为60°的等腰三角形,③一个半径为π的圆,④两条对角线互相垂直平分的四边形,⑤函数y=的图象,其中既是轴对称又是中心对称的图形有( )A、有1个 B、有2个 C、有3个 D、有4个3. 如图的几何体,从左面看的平面图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、x6÷x3=x2 B、(x3)2=x5 C、 D、5. 若式子有意义,则a的取值范围为( )A、 B、 C、且 D、6. 5名同学分别向希望小学捐书3本、5本、4本、3本、6本,其中捐4本的同学后来又追加了3本.追加后的5个数据与之前的5个数据相比( )A、平均数没变 B、中位数没变 C、众数没变 D、方差没变7. 如图,在中, , 则劣弧的度数为( )
4. 下列运算正确的是( )A、x6÷x3=x2 B、(x3)2=x5 C、 D、5. 若式子有意义,则a的取值范围为( )A、 B、 C、且 D、6. 5名同学分别向希望小学捐书3本、5本、4本、3本、6本,其中捐4本的同学后来又追加了3本.追加后的5个数据与之前的5个数据相比( )A、平均数没变 B、中位数没变 C、众数没变 D、方差没变7. 如图,在中, , 则劣弧的度数为( )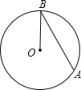 A、106° B、126° C、74° D、53°8. 如图将绕点旋转得到 , 设点的坐标为 , 则A的坐标为( )
A、106° B、126° C、74° D、53°8. 如图将绕点旋转得到 , 设点的坐标为 , 则A的坐标为( )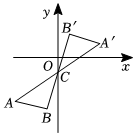 A、 B、 C、 D、9. 如图,在中, , , 分别以A,B两点为圆心,大于为半径画弧,两弧交于M,N两点,直线MN交AC于点D,交于点E,若 , 则AC的长度为( )
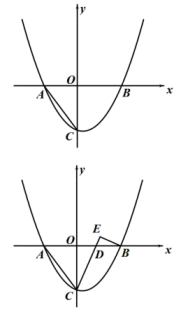
A、 B、 C、 D、9. 如图,在中, , , 分别以A,B两点为圆心,大于为半径画弧,两弧交于M,N两点,直线MN交AC于点D,交于点E,若 , 则AC的长度为( )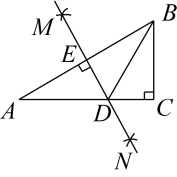 A、9 B、8 C、7 D、610. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线.下列结论:①;②;③;④;⑤.其中含所有正确结论的选项是( )
A、9 B、8 C、7 D、610. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线.下列结论:①;②;③;④;⑤.其中含所有正确结论的选项是( )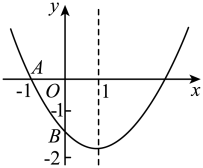 A、①③ B、①③④ C、②④⑥ D、①③④⑤
A、①③ B、①③④ C、②④⑥ D、①③④⑤二、填空题
-
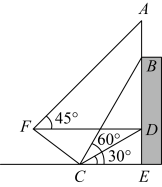
11. 计算.12. 分解因式: =13. 从新冠疫情伊始,很多在外工作的游子为了全民健康没有返乡过年,时隔三年,2023年春节终于可以阖家团圆,2023年春运人流量预计有人次,请将数据用科学记数法表示为.14. 分式方程=1的解为.15. 如图.某同学为测量宣传牌的高度 , 他站在距离教学楼底部E处9米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度的斜坡从C走到F处,此时正好与地面平行.他在F处又测得宣传牌顶部A的仰角为45°,则宣传牌的高度(结果保留根号).
 16. 如图,四边形内接于 , 是直径, , , , 则的直径等于 .
16. 如图,四边形内接于 , 是直径, , , , 则的直径等于 .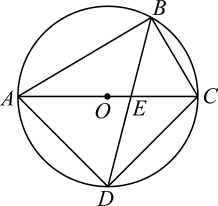 17. 如图,已知是一块含有角的直角三角板,点A是函数的图象上一点,点B是函数的图象上一点,则k的值为 .
17. 如图,已知是一块含有角的直角三角板,点A是函数的图象上一点,点B是函数的图象上一点,则k的值为 .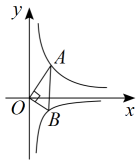 18. 如图,在矩形ABCD中,AB=7,BC=7 , 点P在线段BC上运动(含B、C两点),连接AP,将线段AP绕着点A逆时针旋转60°得到AQ,连接DQ,则线段DQ的最小值为 .
18. 如图,在矩形ABCD中,AB=7,BC=7 , 点P在线段BC上运动(含B、C两点),连接AP,将线段AP绕着点A逆时针旋转60°得到AQ,连接DQ,则线段DQ的最小值为 .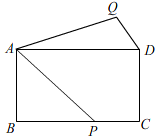
三、解答题
-
19. 先化简,再求值 , 其中.20. 如图,在中,点D是上一点,且 , , 连接交于点F.
 (1)、若 , 求的度数;(2)、若平分 , 求证: .21. 黄石是国家历史文化名城,素有“青铜故里、矿冶之都”的盛名.区域内矿冶文化旅游点有:A.铜绿山古铜矿遗址,B.黄石国家矿山公园,C.湖北水泥遗址博物馆,D.黄石园博园、矿博园.我市八年级某班计划暑假期间到以上四个地方开展研学旅游,学生分成四个小组,根据报名情况绘制了两幅不完整的统计图.
(1)、若 , 求的度数;(2)、若平分 , 求证: .21. 黄石是国家历史文化名城,素有“青铜故里、矿冶之都”的盛名.区域内矿冶文化旅游点有:A.铜绿山古铜矿遗址,B.黄石国家矿山公园,C.湖北水泥遗址博物馆,D.黄石园博园、矿博园.我市八年级某班计划暑假期间到以上四个地方开展研学旅游,学生分成四个小组,根据报名情况绘制了两幅不完整的统计图.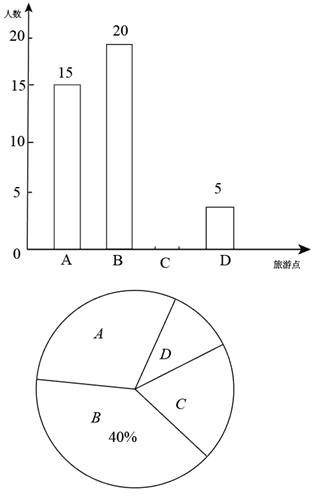
请根据图中信息,解答下列问题:
(1)、全班报名参加研学旅游活动的学生共有人,扇形统计图中A部分所对应的扇形圆心角是;(2)、补全条形统计图;(3)、该班语文、数学两位学科老师也报名参加了本次研学旅游活动,他们随机加入A、B两个小组中,求两位老师在同一个小组的概率.22. 阅读材料,解答问题:已知实数m,n满足 , , 且 , 则m,n是方程的两个不相等的实数根,由韦达定理可知 , .根据上述材料,解决以下问题:(1)、直接应用:已知实数a,b满足: , 且 , 则 , ;(2)、间接应用:在(1)条件下,求的值;(3)、拓展应用:已知实数x,y满足: , 且 , 求的值.23. 某商场主营玩具销售,经市场调查发现,某种玩具的月销量 (件)是售价 (元/件)的一次函数,该玩具的月销售总利润 (售价-进价)×月销量,三者有如下数据:售价 (元/件)
15
20
30
月销量 (件)
500
400
200
月销售总利润 (元)
2500
4000
4000
(1)、试求 关于 的函数解析式( 的取值范围不必写出);(2)、玩具的进价为元/件;当玩具售价 元/件时,月销售总利润有最大值为元.(3)、受市场波动影响,从本月起,该玩具每件的进价上涨 元( ),且物价局规定该玩具售价最高不得超过25元/件.若月销量 与售价 仍满足(1)中的关系,预计本月总利润 最高为3000元,请你求出 的值.