广西壮族自治区贵港市港北区2021-2022学年八年级下学期期中数学试题
试卷更新日期:2023-04-11 类型:期中考试
一、单选题
-
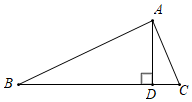
1. 如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
 A、90° B、20° C、45° D、70°2. 在Rt△ABC中, , 点D为斜边AB的中点,若 , 那么AB的长是( )A、4 B、8 C、12 D、243. 如图,已知∠C=∠D=90°,有四个可添加的条件:①AC=BD;②BC=AD;③∠CAB=∠DBA;④∠CBA=∠DAB.能使△ABC≌△BAD的条件有( )
A、90° B、20° C、45° D、70°2. 在Rt△ABC中, , 点D为斜边AB的中点,若 , 那么AB的长是( )A、4 B、8 C、12 D、243. 如图,已知∠C=∠D=90°,有四个可添加的条件:①AC=BD;②BC=AD;③∠CAB=∠DBA;④∠CBA=∠DAB.能使△ABC≌△BAD的条件有( )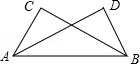 A、1个 B、2个 C、3个 D、4个4. 如图,在中, , , 平分 , 交于点 , 若 , 则的长度等于( )
A、1个 B、2个 C、3个 D、4个4. 如图,在中, , , 平分 , 交于点 , 若 , 则的长度等于( )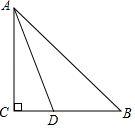 A、 B、 C、2 D、5. 到三角形三边的距离相等的点是( )A、三角形三条高的交点 B、三角形三条中线的交点 C、三角形三条角平分线的交点 D、不存在这个点6. 如图,将 绕点 顺时针旋转角 ,得到 ,若点E恰好在 的延长线上,则 等于( )
A、 B、 C、2 D、5. 到三角形三边的距离相等的点是( )A、三角形三条高的交点 B、三角形三条中线的交点 C、三角形三条角平分线的交点 D、不存在这个点6. 如图,将 绕点 顺时针旋转角 ,得到 ,若点E恰好在 的延长线上,则 等于( )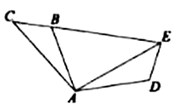 A、 B、 C、 D、7. 如图,P是面积为S的 内任意一点, 的面积为 , 的面积为 ,则( )
A、 B、 C、 D、7. 如图,P是面积为S的 内任意一点, 的面积为 , 的面积为 ,则( )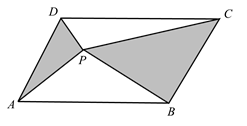 A、 B、 C、 D、 的大小与P点位置有关8. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、等腰三角形 C、平行四边形 D、菱形9. 如图,在 中, 分别是 的中点,点F在 延长线上,添加一个条件使四边形 为平行四边形,则这个条件是( )
A、 B、 C、 D、 的大小与P点位置有关8. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、等腰三角形 C、平行四边形 D、菱形9. 如图,在 中, 分别是 的中点,点F在 延长线上,添加一个条件使四边形 为平行四边形,则这个条件是( )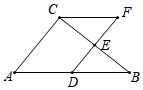 A、 B、 C、 D、10. 如图,点O是矩形ABCD的对角线AC的中点,交AD于点M,若 , , 则OB的长为( )
A、 B、 C、 D、10. 如图,点O是矩形ABCD的对角线AC的中点,交AD于点M,若 , , 则OB的长为( ) A、5 B、4 C、 D、11. 如图,在菱形ABCD中,AC=2 ,BD=2,DH⊥AB于点H,则DH的长为( )
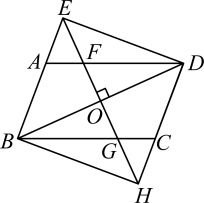
A、5 B、4 C、 D、11. 如图,在菱形ABCD中,AC=2 ,BD=2,DH⊥AB于点H,则DH的长为( )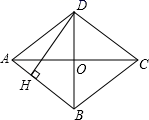 A、3 B、 C、 D、12. 如图,在正方形ABCD中,E为BC上一点,过点E作EFCD,交AD于点F,交对角线BD于点G,取DG的中点H,连接AH,EH,FH.下列结论:①FHAE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD.其中正确的个数是( )
A、3 B、 C、 D、12. 如图,在正方形ABCD中,E为BC上一点,过点E作EFCD,交AD于点F,交对角线BD于点G,取DG的中点H,连接AH,EH,FH.下列结论:①FHAE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD.其中正确的个数是( )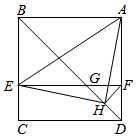 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
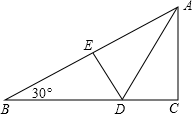
13. 已知等腰三角形的底角为15°,腰长为8cm,则这个三角形的面积为.14. 如图,折叠直角三角形纸片,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是.
 15. 如图,在菱形ABCD中,AC、BD交于点O,AC=4,菱形ABCD的面积为4 ,E为AD的中点,则OE的长为 .
15. 如图,在菱形ABCD中,AC、BD交于点O,AC=4,菱形ABCD的面积为4 ,E为AD的中点,则OE的长为 .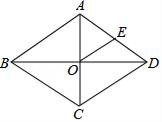 16. 如图,在平行四边形 中, 的平分线与 的平分线交于点E , 若点E恰好在边 上,则 的值为 .
16. 如图,在平行四边形 中, 的平分线与 的平分线交于点E , 若点E恰好在边 上,则 的值为 .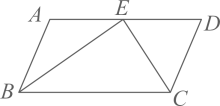 17. 如图,在平行四边形ABCD中, , , 点H、G分别是边DC、BC上的动点,其中点H不与点C重合,连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为.
17. 如图,在平行四边形ABCD中, , , 点H、G分别是边DC、BC上的动点,其中点H不与点C重合,连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为.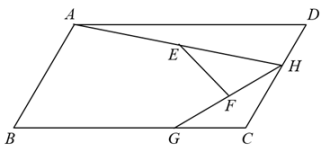 18. 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .
18. 如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .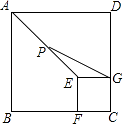
三、解答题
-
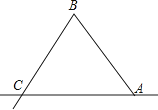
19. 现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
 20. 一个多边形的内角和比它的外角的和的2倍还大180°,求这个多边形的边数.21. 如图,已知 , 是的平分线上一点,交边于点 , , 垂足为点 , 且 , 求的长.
20. 一个多边形的内角和比它的外角的和的2倍还大180°,求这个多边形的边数.21. 如图,已知 , 是的平分线上一点,交边于点 , , 垂足为点 , 且 , 求的长.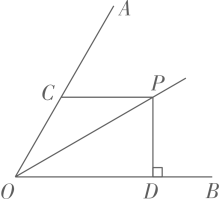 22. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
22. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.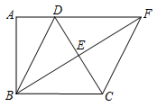 (1)、求证:四边形BCFD是菱形;(2)、若AD=1,BC=2,求BF的长.23. 如图,四边形 是边长为 的菱形,其中对角线 的长为 .
(1)、求证:四边形BCFD是菱形;(2)、若AD=1,BC=2,求BF的长.23. 如图,四边形 是边长为 的菱形,其中对角线 的长为 .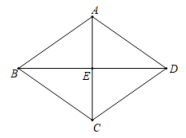
计算:
(1)、对角线 的长度.(2)、菱形 的面积.24. 如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.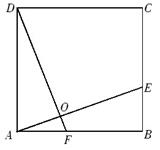 (1)、求证:△DAF≌△ABE;(2)、写出线段AE、DF的数量和位置关系,并说明理由.
(1)、求证:△DAF≌△ABE;(2)、写出线段AE、DF的数量和位置关系,并说明理由.