广西壮族自治区北海市银海区2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在Rt $△ A B C$ 中， $∠ C = 90 °$ ，斜边 $A B = 8$ ，则斜边上的中线 $C D =$ （）

A、2 B、4 C、8 D、16

查看试题解析
3. 下列各组数不是勾股数的是（）

A、0.6，0.8，1 B、7，24，25 C、5，12，13 D、3，4，5

查看试题解析
4. 下列条件中，不能判断四边形是平行四边形的是（）

A、两组对边分别平行 B、一组对边平行，另一组对边相等 C、对角线互相平分 D、一组对边平行，一组对角相等

查看试题解析
5. 一个多边形内角和是 $72 0^{∘}$ ，则这个多边形的边数为（）

A、 $8$ B、 $7$ C、 $6$ D、 $5$

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $A D$ 平分 $∠ B A C$ ，若 $B C = 9$ ，则点D到 $A B$ 的距离是（）

A、2 B、3 C、4.5 D、6

查看试题解析
7. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点O， $∠ A O B = 60 °$ ， $A C = 2$ ，则边 $A B$ 长为（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、1 D、2

查看试题解析
8. 如图，在 $Δ A B C$ 中， $D$ 、 $E$ 分别是 $A B$ 和 $A C$ 两边上的中点，若 $∠ A = 7 5^{∘}$ ， $∠ A D E = 3 5^{∘}$ ，则 $∠ C$ 的度数为（）

A、 $8 0^{∘}$ B、 $7 0^{∘}$ C、 $7 5^{∘}$ D、 $8 5^{∘}$

查看试题解析
9. 如图，在▱ABCD中，∠A=70°，将▱ABCD折叠，使点D，C分别落在点F，E处（点F，E都在AB所在的直线上），折痕为MN，则∠AMF等于（）

A、70° B、40° C、30° D、20°

查看试题解析
10. 如图，P为正方形ABCD的对角线AC上任意一点，PE⊥AB于E，PF⊥BC于F，若AC＝ $\sqrt{2}$ ，则四边形PEBF的周长为（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、2 D、1

查看试题解析

二、填空题

11. 在 $R t △ A B C$ 中，锐角 $∠ A = 50 °$ ，则另一个锐角 $∠ B =$ ．

查看试题解析
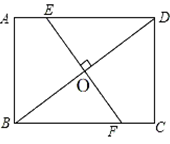
12. 一根旗杆在离地面12米处断裂，旗杆项部落在离旗杆底部5米处.则旗杆折断之前有米.

查看试题解析
13. 在 $△ A B C$ 中，若 $A B = A C = 7$ ， $∠ B = 30 °$ ，则BC边上的高 $A D =$ .

查看试题解析
14. 如图，矩形ABCD中，已知AB=6，BC=8，BD的垂直平分线交AD于点E，交BC于点F，则BF的长为.

查看试题解析
15. 如图，四边形ABCD是菱形，对角线AC，BD相交于点O，AC＝4 $\sqrt{3}$ ， BD＝4，点P是AC上一动点，点E是AB的中点，则PD+PE的最小值为.

查看试题解析

三、解答题

16. 如图，在 $△ A B C$ 和 $△ D C B$ 中， $∠ A = ∠ D = 90 °$ ， $A C = B D$ ， AC与BD相交于点O.
求证： $∠ A C B = ∠ D B C$ .

查看试题解析
17. 如图，已知 $△ A B C$ 的顶点A、B、C在边长为1的方格格点上，画 $△ A B C$ 关于点O中心对称的 $△ A^{'} B^{'} C^{'}$ .

查看试题解析
18. 如图，在 $▱ A B C D$ 中， $∠ A B C = 60 °$ ， BE平分 $∠ A B C$ ，交AD于点E， $A D = 3 c m$ ， $E D = 1 c m$ ，求∠A，∠C，∠D的度数和 $▱ A B C D$ 的周长.

查看试题解析
19. 已知：O是矩形ABCD对角线的交点，E、F、G、H分别是OA、OB、OC、OD上的点，AE＝BF＝CG＝DH，求证：四边形EFGH为矩形

查看试题解析
20. 如图，在 $△ A B C$ 中，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使 $E F = 2 D E$ ，连接CE、AF.
证明： $A F = C E$ .

查看试题解析
21. 如图，某中学有一块四边形的空地ABCD，学校计划在空地上种植草皮，经测量 $∠ B = 90 °$ ， $A B = 3$ 米， $B C = 4$ 米， $C D = 12$ 米， $A D = 13$ 米，若每平方米草皮需要300元，问学校需要投入多少资金买草皮？

查看试题解析
22. 如图，等边 $Δ A E F$ 的顶点 $E$ ， $F$ 在矩形 $A B C D$ 的边 $B C$ ， $C D$ 上，且 $∠ C E F = 45^{\circ}$ .
求证：矩形 $A B C D$ 是正方形.

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，过点C的直线 $M N ∥ A B$ ， D为AB边上一点，过点D作 $D E ⊥ B C$ ，交直线MN于点E，垂足为点F，连接CD，BE.

(1)、若 $A D = 4 c m$ ，求CE的长；

(2)、当点D为AB的中点时，四边形BECD是什么特殊四边形？说明你的理由；

(3)、若点D为AB的中点，当 $∠ A$ 的大小满足什么条件时，四边形BECD是正方形？请直接写出答案.

查看试题解析