广西壮族自治区北海市合浦县2021-2022学年八年级下学期期中数学试题
试卷更新日期：2023-04-11 类型：期中考试
一、单选题
-
1. 下列图形中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列各组数中，是勾股数的是（ ）A、1， ， 2 B、0.3，0.4，0.5 C、8，15，17 D、5， 6，73. 已知一个正多边形的内角是140°，则它是几边形（ ）A、10 B、9 C、8 D、74. 用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上，分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是（ ）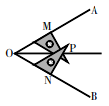
A、SAS B、SSS C、ASA D、HL5. 如图，在ABCD中，AB=3，AD=5，∠ABC的平分线BE交AD于点E，则DE的长是（ ）.
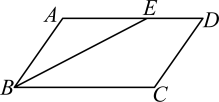A、4 B、3 C、3.5 D、26. 如图，小明和小华同时从P处分别向北偏东60°和南偏东30°方向出发，他们的速度分别是3m/s和4m/s，则20s后他们之间的距离为（ ）
A、80m B、100m C、120m D、140m7. 如图，已知四边形是平行四边形，下列结论中正确的是（ ）
A、当时，它是矩形 B、当时，它是矩形 C、当时，它是正方形 D、当时，它是菱形8. 如图，O是矩形 的对角线 的中点，E是 边的中点.若 ，则线段 的长为（ ）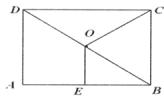
A、3 B、4 C、5 D、69. 如图，已知矩形ABCD中，R，P分别是DC、BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（ ）
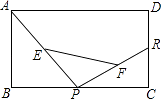A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定10. 如图，在△ABC中，∠ABC=60°，BC=20，点D在边AB上，CA=CD，BD=8，则AD=（ ）
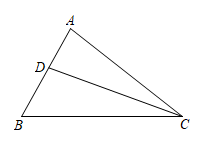A、2 B、3 C、4 D、6二、填空题
-
11. 已知：如图，四边形AEFD和EBCF都是平行四边形，则四边形ABCD是.
12. 如图，在△ABC中，∠C＝90°，AD平分∠CAB，BD＝4cm，点D到AB的距离为2cm，则BC＝cm.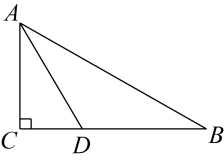
13. 如图所示，在正方形ABCD中，AC，BD相交于点O， AOE绕点O逆时针旋转90°后与 BOF重合，AB＝2，则四边形BEOF面积是 ．
14. 菱形ABCD的面积为24，对角线AC的长为6，则对角线BD的长为 .15. 如图，在锐角△ABC中，AB＝2，∠BAC＝60°，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM+MN的最小值是.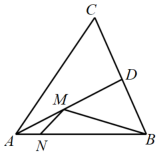
三、解答题
-
16. 如图，已知Rt△ABC中，∠B＝90°，∠A＝30°，请用尺规作图法，在AC边上求作一点D，使BD＝AC.（保留作图痕迹，不写作法）
17. 小明是这样画平行四边形的：如图，将三角尺的一边贴着直尺推移到的位置，这时四边形就是平行四边形.你能说说小明这样做的道理吗？
18. 如图，已知点D是BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F，连接AD，若AD垂直平分EF，求证：AD是△ABC的角平分线.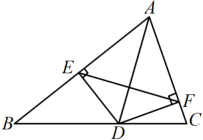
19. 在△ABC中，AB＝AC，CD⊥AB于D.
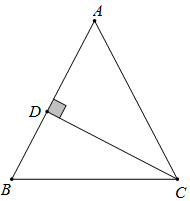(1)、若∠A＝40°，求∠DCB的度数；(2)、若BC＝15，CD＝12，求AC的长.20. 如图，在▱ABCD中，作对角线BD的垂直平分线EF，垂足为O，分别交AD，BC于E，F，连接BE，DF．求证：四边形BFDE是菱形．
