广西壮族自治区百色市教研室2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-04-11 类型:期中考试
一、单选题
-
1. 计算:( )A、0 B、1 C、-2022 D、20222. 下列四个实数中,是无理数的是( )A、 B、 C、3.14 D、1.0100100013. 下列说法正确的是( )A、-4的平方根是 B、的算术平方根是 C、的平方根是 D、0的平方根与算术平方根都是04. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将0.00000201用科学记数法表示为( )A、 B、 C、 D、5. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、6. 三个数 , , 的大小关系是( )A、 B、 C、 D、7. 下列各式计算正确的是( )A、 B、 C、 D、8. 不等式组 的解集在数轴上表示正确的是( )A、
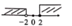 B、
B、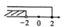 C、
C、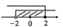 D、
D、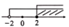 9. 如图是一个数值转换机,若输入a的值为4,则输出的结果应为( )
9. 如图是一个数值转换机,若输入a的值为4,则输出的结果应为( ) A、2 B、 C、1 D、10. 已知数a在数轴上的位置如图所示,则化简的结果为( ).
A、2 B、 C、1 D、10. 已知数a在数轴上的位置如图所示,则化简的结果为( ). A、 B、3 C、 D、11. 某次知识竞赛共20道题,每一题答对得10分,答错或不答都扣5分,小芳得分不低于80分.设她答对了x道题,则根据题意可列出不等式为( )A、10x-2(20-x)≥80 B、10x-(20-x)>80 C、10x-5(20-x)≥80 D、10x-5(20-x)>8012. 如果不等式组的解集是x>4,那么n的取值范围是( )A、n≥4 B、n≤4 C、n=4 D、n<4
A、 B、3 C、 D、11. 某次知识竞赛共20道题,每一题答对得10分,答错或不答都扣5分,小芳得分不低于80分.设她答对了x道题,则根据题意可列出不等式为( )A、10x-2(20-x)≥80 B、10x-(20-x)>80 C、10x-5(20-x)≥80 D、10x-5(20-x)>8012. 如果不等式组的解集是x>4,那么n的取值范围是( )A、n≥4 B、n≤4 C、n=4 D、n<4二、填空题
-
13. 化简: = .14. x的与2的差为正数,用不等式表示为.15. 化简 的结果是.16. 关于a的不等式的解集在数轴上表示如图所示,则该不等式的解集为.
 17. 对于非负实数x “四舍五入”到个位的值记为 , 即当m为非负整数时,若 , 则. 如: , , ……根据以上材料,若 , 则x应满足的条件是.18. 如图,现有正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为 , 宽为的大长方形,那么需要C类卡片的张数是;
17. 对于非负实数x “四舍五入”到个位的值记为 , 即当m为非负整数时,若 , 则. 如: , , ……根据以上材料,若 , 则x应满足的条件是.18. 如图,现有正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为 , 宽为的大长方形,那么需要C类卡片的张数是;
三、解答题
-
19. 计算:20. 计算:21. 解不等式 , 并写出它的所有正整数解.22. 解不等式组 , 并把它的解集表示在数轴上.
 23. 先化简,再求值: , 其中.24. 如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.
23. 先化简,再求值: , 其中.24. 如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化. (1)、求绿化的面积.(用含a、b的代数式表示)(2)、当a=2,b=4时,求绿化的面积.25. 先阅读,再解题:
(1)、求绿化的面积.(用含a、b的代数式表示)(2)、当a=2,b=4时,求绿化的面积.25. 先阅读,再解题:解不等式:>0.
解:根据两数相除,同号得正,异号得负,得
①>0或②解不等式组①,得x>3,解不等式组②,得x<-.
所以原不等式的解集为x>3或x<-.
参照以上解题过程所反映的解题思想方法,试解不等式:<0.
26. 红星中学计划组织“春季研修活动,活动组织负责人从公交公司了解到如下租车信息:车型
载客量(人/辆)
48
30
租金(元/辆)
400
280
校方从实际情况出发,决定租用 、 型客车共5辆,而且租车费用不超过1900元.
(1)、请为校方设计可能的租车方案;(2)、在(1)的条件下,校方根据自愿的原则,统计发现有193人参加,请问校方应如何租车,且又省钱?