鲁教版(五四制)2022-2023学年度第二学期七年级数学 三角形内角和定理 期中复习
试卷更新日期:2023-04-10 类型:复习试卷
一、单选题
-
1. 如图, , AE⊥EF,E在BC上,过E作EC⊥DC,EG平分∠FEC,ED平分∠AEC.若∠EAD+∠BAD=180°,∠EDA=3∠CEG,则下列结论:①∠EAB=2∠FEG;②∠AED=45°+∠GEF;③∠EAD=135°-4∠GEC;④∠EAB=15°,其中正确的是( )
 A、①②③④ B、①③④ C、①②④ D、①②③2. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A、①②③④ B、①③④ C、①②④ D、①②③2. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )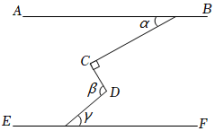 A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°3. 如图,在△ABC中,∠C=90°, , 将△ABC沿直线m翻折,点A落在点D的位置,则的度数是( )
A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°3. 如图,在△ABC中,∠C=90°, , 将△ABC沿直线m翻折,点A落在点D的位置,则的度数是( ) A、30° B、45° C、60° D、75°4. 如图,三角板的直角顶点在直尺的一边上.若∠1=30°,∠2=70°,则∠3的度数是( )
A、30° B、45° C、60° D、75°4. 如图,三角板的直角顶点在直尺的一边上.若∠1=30°,∠2=70°,则∠3的度数是( ) A、30° B、40° C、50° D、60°5. 如图,l1∥l2 , 则( )
A、30° B、40° C、50° D、60°5. 如图,l1∥l2 , 则( ) A、α+β-γ=180° B、α+β+γ=180° C、α+β=2γ D、α+β=γ6. 如图,直线 , 如果 , , 那么的度数是( )
A、α+β-γ=180° B、α+β+γ=180° C、α+β=2γ D、α+β=γ6. 如图,直线 , 如果 , , 那么的度数是( ) A、31° B、40° C、39° D、70°7. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( )
A、31° B、40° C、39° D、70°7. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( ) A、 B、 C、 D、8. 如图,若 , , , 则的度数是( )
A、 B、 C、 D、8. 如图,若 , , , 则的度数是( )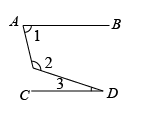 A、25° B、30° C、36° D、38°9. 如图摆放着一副三角板,∠B=∠EDF=90°,点E在AC上,点D在BC的延长线上, , ∠A=30°,∠F=45°,则∠CED的度数为( )
A、25° B、30° C、36° D、38°9. 如图摆放着一副三角板,∠B=∠EDF=90°,点E在AC上,点D在BC的延长线上, , ∠A=30°,∠F=45°,则∠CED的度数为( ) A、15° B、20° C、30° D、45°10. 如图,的两条角平分线 , 交于点P,若 , 则为( )
A、15° B、20° C、30° D、45°10. 如图,的两条角平分线 , 交于点P,若 , 则为( ) A、112° B、115° C、120° D、125°
A、112° B、115° C、120° D、125°二、填空题
-
11. 如图,已知∠1=∠2,∠B=30°,则∠3=°.
 12. 如图,将一个含有30°角的直角三角板ABC的直角顶点放在两条平行线 , 中的上,若 , 则∠2的度数为 .
12. 如图,将一个含有30°角的直角三角板ABC的直角顶点放在两条平行线 , 中的上,若 , 则∠2的度数为 .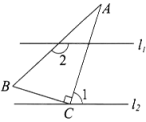 13. 如图,有一个三角形纸片ABC,∠A=65°,∠B=75°,将纸片一角折叠,使点C落在△ABC外的C'点处,若∠DFC'=20°,则∠BED的大小为.
13. 如图,有一个三角形纸片ABC,∠A=65°,∠B=75°,将纸片一角折叠,使点C落在△ABC外的C'点处,若∠DFC'=20°,则∠BED的大小为. 14. 如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为 .
14. 如图,AB∥CD,CF平分∠DCG,GE平分∠CGB交FC的延长线于点E,若∠E=34°,则∠B的度数为 . 15. 如图,中, , D、E是AC边上的点,把沿BD对折得到 , 再把沿BE对折得到 , 若恰好落在BD上,且此时 , 则 .
15. 如图,中, , D、E是AC边上的点,把沿BD对折得到 , 再把沿BE对折得到 , 若恰好落在BD上,且此时 , 则 .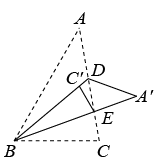
三、解答题
-
16. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.
 17. 如图,在中, , , AD是的角平分线,求的度数.
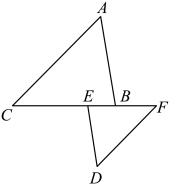
17. 如图,在中, , , AD是的角平分线,求的度数. 18. 已知:如图,点C、E、B、F在一条直线上, , ∠A=∠D.
18. 已知:如图,点C、E、B、F在一条直线上, , ∠A=∠D.求证: .
四、综合题
-
19. 如图,在中,于点 , 于点 , .
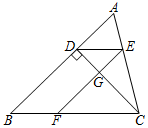 (1)、请说明DE∥BC;(2)、若∠A=60°,∠ACB=72°,求∠CDE的度数.20. 如图,已知 , , 点E在线段BC的延长线上,AE平分 , 连接DE, , .
(1)、请说明DE∥BC;(2)、若∠A=60°,∠ACB=72°,求∠CDE的度数.20. 如图,已知 , , 点E在线段BC的延长线上,AE平分 , 连接DE, , . (1)、求证;(2)、求的度数.21. 如图,直线 , 点E,G在直线AB上,点F,H在直线CD上,∠1+∠2=180°.
(1)、求证;(2)、求的度数.21. 如图,直线 , 点E,G在直线AB上,点F,H在直线CD上,∠1+∠2=180°.
 (1)、如图1,求证:;(2)、如图2,若∠1=120°,GM平分∠BGH,FM平分∠EFH,设FM与GH相交于点O.求∠FOH的度数.
(1)、如图1,求证:;(2)、如图2,若∠1=120°,GM平分∠BGH,FM平分∠EFH,设FM与GH相交于点O.求∠FOH的度数.