鲁教版(五四制)2022-2023学年度第二学期七年级数学 平行线的性质定理 期中复习
试卷更新日期:2023-04-10 类型:复习试卷
一、单选题
-
1. 下列说法正确的是( )A、内错角相等 B、平面内,过一点有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、过一点有且只有一条直线与已知直线平行2. 将一副直角三角板按如图所示的方式叠放在一起,若AC∥DE,则∠BAE的度数为( )
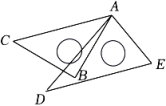 A、50° B、65° C、75° D、85°3. 如图,AB∥CD,EF交AB于点G,EM平分∠CEF,∠FGB=60°,则∠GME的度数为( )
A、50° B、65° C、75° D、85°3. 如图,AB∥CD,EF交AB于点G,EM平分∠CEF,∠FGB=60°,则∠GME的度数为( ) A、60° B、55° C、50° D、45°4. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A、60° B、55° C、50° D、45°4. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )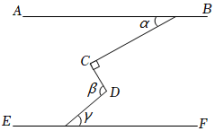 A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°5. 如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°5. 如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )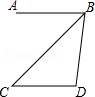 A、90° B、100° C、110° D、120°6. 下列命题中,是真命题的是( )A、同位角相等 B、有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、邻补角一定互补7. 下列语句:
A、90° B、100° C、110° D、120°6. 下列命题中,是真命题的是( )A、同位角相等 B、有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、邻补角一定互补7. 下列语句:①若三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )
A、①②是真命题 B、②③是真命题 C、①③是真命题 D、以上结论皆是假命题8. 如图,AB//CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )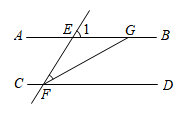 A、122° B、151° C、116° D、97°9. 如图,AB//CD,那么∠A+∠C+∠AEC=( )
A、122° B、151° C、116° D、97°9. 如图,AB//CD,那么∠A+∠C+∠AEC=( )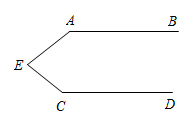 A、360° B、270° C、200° D、180°10. 如图, , 直线分别交、于E、F两点,若 , 则等于( )
A、360° B、270° C、200° D、180°10. 如图, , 直线分别交、于E、F两点,若 , 则等于( )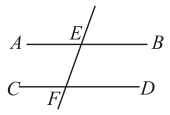 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图消防云梯,其示意图如图1所示,其由救援台AB,延展臂BC(B在C的左侧)、伸展主臂CD,支撑臂EF构成,在作业过程中,救援台AB、车身GH及地面MN三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂BC与支摚臂EF所在直线互相垂直,且∠EFH=69°,则这时展角∠ABC= .
 12. 如图,ABCD为一长条形纸带, , 将ABCD沿EF折叠,A、D两点分别与A′、D′ 对应,若∠1=2∠2,则∠2的度数为度.
12. 如图,ABCD为一长条形纸带, , 将ABCD沿EF折叠,A、D两点分别与A′、D′ 对应,若∠1=2∠2,则∠2的度数为度. 13. 如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2=°;
13. 如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2=°; 14. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果 , 那么的度数为.
14. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果 , 那么的度数为. 15. 如图,在平行线a,b之间放置一个直角三角形,三角形的顶点A,C分别在直线a,b上,∠ACB=90°,∠BAC=30°,则∠1+∠2= .
15. 如图,在平行线a,b之间放置一个直角三角形,三角形的顶点A,C分别在直线a,b上,∠ACB=90°,∠BAC=30°,则∠1+∠2= .
三、解答题
-
16. 如图,直线 , 平分 , , 垂足为点 , = , 求的度数.
 17. 如图,已知 , , 试说明: . (写出推理过程,不写理由)
17. 如图,已知 , , 试说明: . (写出推理过程,不写理由) 18. 完成下列证明:
18. 完成下列证明:如图,已知于点 , 于点 , 于点 , ,

求证: .
证明: , 已知 ,
▲ ,
▲ 两直线平行,内错角相等 ,
, 已知 ,
_▲ ,
,
已知 ,
.
四、综合题
-
19. 如图,= , = .
 (1)、求证:=;(2)、判定与的位置关系,并说明理由.20. 如图,AB∥CD,∠1=∠2.
(1)、求证:=;(2)、判定与的位置关系,并说明理由.20. 如图,AB∥CD,∠1=∠2. (1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.21. 如图,AB∥CD,点E为两直线之间的一点.
(1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.21. 如图,AB∥CD,点E为两直线之间的一点. (1)、如图1,若∠BAE=30°,∠DCE=20°,则∠AEC=;
(1)、如图1,若∠BAE=30°,∠DCE=20°,则∠AEC=;如图1,若∠BAE=α,∠DCE=β,则∠AEC=;
(2)、如图2,试说明,∠BAE+∠AEC+∠ECD=360°;(3)、如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC的数量关系,并说明理由.22. 已知:如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°. (1)、试说明:ABCD;(2)、试探究DF与DB的数量关系,并说明理由.23. 如图1,直线AB与直线l1 , l2分别交于C,D两点,点M在直线l2上,射线DE平分∠ADM交直线l1于点Q,∠ACQ=2∠CDQ.
(1)、试说明:ABCD;(2)、试探究DF与DB的数量关系,并说明理由.23. 如图1,直线AB与直线l1 , l2分别交于C,D两点,点M在直线l2上,射线DE平分∠ADM交直线l1于点Q,∠ACQ=2∠CDQ.

图1 图2
(1)、求证:l1∥l2 .(2)、如图2,射线QP交直线l2于点F,交线段CD于点P,且∠ACQ=70°.①若∠QFD=20°,直接写出∠FQD的度数.
②点N在射线DE上,满足∠QCN=∠QFD,连接CN,请补全图形,探究∠CND与∠FQD满足的等量关系,并说明理由.