鲁教版（五四制）2022-2023学年度第二学期七年级数学 平行线的判定定理 期中复习

试卷更新日期：2023-04-10 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 下列说法正确的是（ ）
    A、内错角相等 B、平面内，过一点有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、过一点有且只有一条直线与已知直线平行

    查看试题解析

  • 2. 如图，下列条件中不能判定AB∥CD的是（    ）

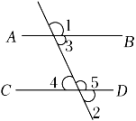    A、∠1＝∠2 B、∠3＝∠4 C、∠3+∠5＝180° D、∠2＝∠3

    查看试题解析

  • 3. 直线a、b、c中，a∥b，b∥c，则直线a与直线c的关系是（   ）
    A、相交 B、平行 C、垂直 D、不确定

    查看试题解析

  • 4. 如下图，下列条件能判断两直线AB，CD平行的是（   ）

    A、∠1＝∠2 B、∠3＝∠4 C、∠1＝∠5 D、∠3＝∠5

    查看试题解析

  • 5. 如图，AB∥EF，∠C＝90°，则α、β、γ的关系为（   ）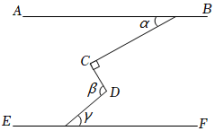

    A、α+β-γ＝90° B、β＝α+γ    C、α+β+γ＝180° D、β+γ-α＝90°

    查看试题解析

  • 6. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（   ）

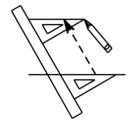    A、两直线平行，同旁内角相等 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、同位角相等，两直线平行

    查看试题解析

  • 7. 如图，AB//CD，那么∠A+∠C+∠AEC＝（   ）

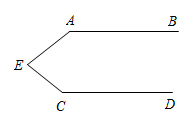    A、360° B、270° C、200° D、180°

    查看试题解析

  • 8. 如图，不能推出a∥b的条件是（   ）

    A、∠1=∠3 B、∠2+∠3=180° C、∠2=∠4 D、∠1=∠4

    查看试题解析

  • 9. 如图，点E在AC的延长线上，下列条件不能判定AB∥CD的是（   ）

    A、∠1=∠2 B、∠3=∠4 C、∠A=∠DCE D、∠A+∠2+∠4=180°

    查看试题解析

  • 10. 如图，已知∠B＝∠AEF，则（ ）

    A、EF∥BC B、AD∥EF C、AD∥BC D、AB∥CD

    查看试题解析

二、填空题

  • 11. 如图，一条公路修到湖边时，需拐弯绕湖而过，在A，B，C三处经过三次拐弯，此时道路恰好和第一次拐弯之前的道路平行（即AE∥CD），若∠A＝100°，∠B＝160°，则∠C的度数是 .

    查看试题解析

  • 12. 如图，在图中标注的∠1、∠3、∠4、∠5中，当∠2 =∠时， AE∥BF.

    查看试题解析

  • 13. 如图，直线l1∥l2 ， AQ平分∠DAC，∠1＝50°，∠2＝25°，则∠3＝°．

    查看试题解析

  • 14. 如图，直线l1∥l2 ， ∠α=∠β ， ∠1=40° ， 则∠2=°.

    查看试题解析

  • 15. 如图表示钉在一起的木条a，b，c．若测得∠1＝50°，∠2＝75°，要使木条a//b，木条a至少要旋转°．

    查看试题解析

三、解答题

  • 16. 已知：如图，点E，F是BD上的点，∠AED=∠CFB，AE=CF，BE=DF．

    求证：AB∥CD，AB=CD．

    查看试题解析

  • 17. 已知：点A、E、D、C在同一条直线上，AE=CD ， EF//BD ， EF=BD.求证：AB//CF.

    查看试题解析

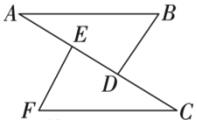  • 18. 完成下面的证明：如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β＝90°，求证：AB∥CD．

    完成推理过程：

    BE平分∠ABD（已知），

    ∴∠ABD＝2∠α（  ）．

    ∵DE平分∠BDC（已知），

    ∴∠BDC＝2∠β（  ）

    ∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β）（  ）

    ∵∠α+∠β＝90°（已知），

    ∴∠ABD+∠BDC＝180°（  ）．

    ∴AB∥CD（  ）．

    查看试题解析

四、综合题

  • 19. 如图，AB∥CD，试探讨四个图形中∠APC与∠PAB，∠PCD的数量关系.

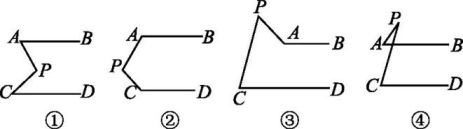    (1)、图①中∠APC与∠PAB，∠PCD的数量关系是；
    (2)、图②中∠APC与∠PAB，∠PCD的数量关系是；
    (3)、请你在图③和图④中任选一个，说出∠APC与∠PAB，∠PCD的数量关系，并说明理由.

    查看试题解析

  • 20. 如图，B，F，E，C在同一条直线上，∠A＝∠D．

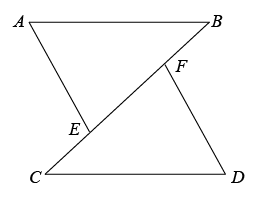    (1)、若∠A＝78°，∠C＝47°，求∠BFD的度数．
    (2)、若∠AEB+∠BFD＝180°，求证：AB∥CD．

    查看试题解析

  • 21. 如图1，BD是△ABC的角平分线，作∠BDE = ∠ABD交AB于点E．

    (1)、求证：ED∥BC；
    (2)、若AC⊥BD，点M为线段AC延长线上一点（不与点c重合），连接BM，若AB⊥BM，在图2中补全图形并证明：∠DBC = ∠BMA．

    查看试题解析

  • 22. 如图，B，F，E，C在同一条直线上，∠A＝∠D．

    (1)、若∠A＝78°，∠C＝47°，求∠BFD的度数．
    (2)、若∠AEB+∠BFD＝180°，求证：AB∥CD．

    查看试题解析

  • 23. 问题情境：

    我们知道，“如果两条平行直线被第三条直线所截，截得的同位角相等，内错角相等，同旁内角互补”，所以在某些探究性度量中通过“构造平行线”可以起到转化角的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE//GF．

    问题初探：

    如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，则∠EMC的度数是多少呢？若过点C作CH//GF，则CH//DE，这样就将∠CAF转化为∠HCA，∠EMC转化为∠MCH，从而可以求得∠EMC的度数为…．

    (1)、请你直接写出：∠CAF＝°，∠EMC＝°．
    (2)、类比再探：若将将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想∠EMC与∠CAF的数量关系？并说明理由．

     

    (3)、方法迁移：请你猜想（1）（2）解决问题的思路，在图（2）中探究∠BAG与∠BMD的数量关系？并说明理由．

    查看试题解析