山东省滨城高中联盟2022-2023学年高一下学期物理3月月考试卷

试卷更新日期：2023-04-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，场地自行车赛道设计成与水平面保持一定倾角，三位运动员骑自行车在赛道转弯处做匀速圆周运动，则下列说法正确的是（　　）

A、三位运动员可能受重力、支持力、向心力的作用 B、若此时三位运动员线速度大小相等，则他们所需要向心力的大小关系一定满足 $F_{A} < F_{B} < F_{C}$ C、若此时三位运动员角速度相等，则他们的向心加速度大小关系满足 $a_{A} > a_{B} > a_{C}$ D、若运动员突然加速，仍然可以保持原轨道做匀速圆周运动，则自行车受到的支持力会减小

查看试题解析
2. 如图所示，飞机在空中飞行沿着曲线ab斜向上减速运动，则飞机飞行到c点时受到的合外力F的方向可能正确的是（）

A、 B、 C、 D、

查看试题解析
3. 如图所示，轻绳一端连在水平台上的玩具小车上、一端跨过光滑定滑轮系着皮球（轻绳延长线过球心）。小车牵引着绳使皮球沿光滑竖直墙面从较低处上升，则在球匀速上升且未离开竖直墙面的过程中（　　）

A、绳对球的拉力逐渐减小 B、球对墙的压力大小不变 C、玩具小车做加速运动 D、玩具小车做㓕速运动

查看试题解析
4. 由于空气阻力的影响，炮弹的实际飞行轨迹不是抛物线，而是“弹道曲线”，如图中实线所示，图中虚线为不考虑空气阻力情况下炮弹的理想运动轨迹。O、a、b、c、d为弹道曲线上的五点，其中O点为发射点，d点为落地点，b点为轨迹的最高点，a、c为运动过程中经过的距地面高度相等的两点，重力加速度为 $g$ 。下列说法正确的是（　　）

A、炮弹到达最高点b时的加速度为 $g$ B、炮弹经过c点时的加速度方向沿该点切线斜向上 C、炮弹经过a点时加速度的竖直分量大于 $g$ D、炮弹由a点运动到b点的时间与由b点运动到c点的时间相等

查看试题解析
5. 探究向心力的大小 $F_{n}$ 与小球质量 $m$ 、角速度 $ω$ 和标尺半径 $r$ 之间关系的实验装置如图所示，已知挡板A、B、C到转轴距离之比为 $1 ： 2 ： 1$ 。某次实验选用质量相同的小球分别放在变速塔轮的长槽挡板A处和短槽挡板C处，当塔轮匀变速转动时左右两标尺露出的格子数之比为 $1 ： 4$ 。则传动手柄皮带所用的左右两侧塔轮圆盘半径之比为（　　）

A、 $2 ： 1$ B、 $1 ： 2$ C、 $4 ： 1$ D、 $1 ： 4$

查看试题解析
6. 如图所示，一辆小车静止在水平地面上，车内固定着一个倾角为60°的光滑斜面 $O A$ ，光滑挡板 $O B$ 与水平方向的夹角为 $θ$ ，挡板 $O B$ 可绕转轴 $O$ 在竖直平面内转动。现将重为 $G$ 的圆球放在斜面与挡板之间。下列说法错误的是（　　）

A、若 $θ = 60 °$ ，球对斜面的压力大小为 $G$ B、若挡板 $O B$ 从 $θ = 30 °$ 位置沿逆时针方向缓慢转动到 $θ = 90 °$ 过程中，则球对斜面的压力逐渐增大 C、若 $θ = 30 °$ ，使小车水平向左做变加速运动，则小车对地面的压力增大 D、若 $θ = 60 °$ ，使小车水平向右做匀加速直线运动，则球对挡板的压力可能为零

查看试题解析
7. 如图所示，质量为 $m$ 的小球置于正方体的光滑盒子中，盒子的边长略大于球的直径。某同学拿着该盒子在竖直平面内做半径为 $R$ 的匀速圆周运动，已知重力加速度为 $g$ ，空气阻力不计，要使在最高点时盒子与小球之间恰好无作用力，则（　　）

A、该盒子做圆周运动的向心力恒定不变 B、该盒子做匀速圆周运动的周期一定等于 $2 π \sqrt{\frac{g}{R}}$ C、盒子在最低点时，小球对盒子的作用力大小等于 $6 m g$ D、盒子在与 $O$ 点等高的右侧位置时，小球对盒子的作用力大小等于 $\sqrt{2} m g$

查看试题解析

二、多选题

8. 如图所示，A、B、C三个小球的质量分别为 $3 m$ 、 $2 m$ 、 $m$ ，轻质弹簧一端固定在斜面顶端，另一端与 $A$ 球相连，A、B间固定一个轻杆，B、C间由一轻质细线连接，倾角为 $θ$ 的光滑斜面固定在地面上，弹簧、轻杆与细线均平行于斜面，初始系统处于静止状态，细线被烧断的瞬间，下列说法正确的是（　　）

A、A球的受力情况未变，加速度为零 B、C球的加速度沿斜面向下，大小为 $g s i n θ$ C、A，B两个小球的加速度均沿斜面向上，大小均为 $\frac{g s i n θ}{3}$ D、A，B之间杆的拉力大小为 $\frac{12 m g s i n θ}{5}$

查看试题解析
9. 2022年2月18日，我国运动员夺得北京冬奥会自由式滑雪女子U型场地技巧赛冠军。比赛场地可简化为如图甲所示的模型：滑道由两个半径相同的四分之一圆柱面轨道连接而成，轨道的倾角为 $θ$ 。某次腾空时，运动员（视为质点）以大小为 $v$ 的速度从轨道边缘上的 $M$ 点沿轨道的竖直切面 $A B C D$ 滑出轨道，速度方向与轨道边缘 $A D$ 的夹角为 $90 ° - θ$ ，腾空后沿轨道边缘 $A D$ 上的 $N$ 点进入轨道，腾空过程（从 $M$ 点运动到 $N$ 点的过程）的左视图如图乙所示。重力加速度大小为 $g$ ，不计空气阻力。下列说法正确的是（　　）

A、运动员腾空过程中处于超重状态 B、运动员腾空过程中离开 $A D$ 的最大距离为 $\frac{v^{2} c o s θ}{2 g}$ C、运动员腾空的时间为 $\frac{2 v}{g}$ D、 $M$ 、 $N$ 两点的距离为 $\frac{4 v^{2} s i n θ}{g}$

查看试题解析
10. 如图所示，水平圆盘可绕竖直轴转动，圆盘上的物体A、B、C的质量分别为m、2m、3m，A叠放在B上，C、B离圆心O距离分别为2r、3r，C、B之间用细线相连。圆盘静止时细线刚好拉直。已知C、B与圆盘间的动摩擦因数均为μ，A、B间的动摩擦因数为4μ，设最大静摩擦力等于滑动摩擦力，重力加速度大小为g，现让圆盘从静止缓慢加速转动，直到有木块即将发生相对滑动为止。用ω表示圆盘转动的角速度，下列说法正确的是（）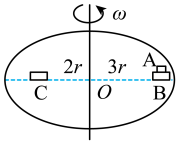

A、当 $ω \leq \sqrt{\frac{μ g}{3 r}}$ 时，轻绳的拉力为零 B、B木块与转台间摩擦力一直增大 C、当 $ω = \sqrt{\frac{μ g}{r}}$ 时，C木块与转台间摩擦力为零 D、ω的最大值为 $ω_{m} = \sqrt{\frac{2 μ g}{r}}$

查看试题解析

三、实验题

11. 为探究向心力大小与半径、角速度、质量的关系。某实验小组通过如图甲所示装置进行实验。滑块套在水平杆上，随水平杆一起绕竖直杆做匀速圆周运动，力传感器通过一细绳连接滑块。用来测量向心力 $F$ 的大小。滑块上固定一遮光片，测得质量为 $m$ ，遮光片宽度为 $d$ ，光电门可以记录遮光片通过的时同，测得旋转半径为r，滑块随杆匀速圆周运动，每经过光电门一次，通过力传感器和光电门就同时获得一组向心力 $F$ 和角
速度 $ω$ 的数据。

(1)、为了深究向心力与角度的关系，需要控制和保持不变，某次旋转过程中遮光片经过光电门时的遮光时间为 $Δ r$ ，则角速度 $ω =$ 。

(2)、以 $F$ 为纵坐标，以 $\frac{1}{Δ t^{2}}$ 为横坐标，可在坐标纸中指出数据点作一条如图乙所示直线，图线不过坐标原点的原因是。

查看试题解析
12. 某学习小组设计如下实验研究平抛运动。如图1所示，弯曲轨道 $A B$ 固定在水平桌面上，在离轨道边缘 $B$ 不远处有一可移动的竖直平面 $a b c d$ ，平面中心竖直线标有刻度，0刻度线与桌面边缘平齐。以边缘 $B$ 正下方的 $O$ 点为原点建立水平 $x$ 轴。实验时，将竖直平面移动到处 $x$ ，从固定立柱处由静止释放体积很小的钢珠，钢珠从 $B$ 点离开后击中中心竖直线某点，记录刻度值 $y$ ；改变 $x$ ，重复试验。

(1)、研究平抛运动规律时，下述条件对减小误差没有帮助的是____。

A、弯曲轨道边缘保持水平 B、弯曲轨道尽量光滑 C、保持竖直平面 $a b c d$ 与水平面垂直 D、重复实验时，每次都要保证释放位置为立柱处

(2)、如图所示的图像中，能正确反映 $y$ 与 $x$ 的关系的是____。

A、 B、 C、

(3)、若某次将钢珠从固定立柱处由静止释放，记录钢珠击中中心竖直线的刻度，记为 $y$ ；将竖直平面向远离 $B$ 方向平移 $10.00 c m$ ，再次将钢珠从固定立柱处由静止释放，记录钢珠击中中心竖直线的刻度为 $y_{1} = y + 5.02 c m$ ；将竖直平面再向远离 $B$ 方向平移 $10.00 c m$ ，让钢珠从固定立柱处由静止释放，记录钢珠击中中心竖直线的刻度为 $y_{2} = y + 19.84 c m$ 。钢珠的初速度为 $v_{0} =$ $m / s$ 。（结果保留两位有效数字）

查看试题解析

四、解答题

13. 冲关节目是一种户外娱乐健康游戏，如图所示为参赛者遇到的一个关卡。一个半径为R的圆盘浮在水面上，圆盘表面保持水平且与水平跑道的高度差 $h = 1.25 m$ ， M为圆盘边缘上一点。某时刻，参赛者从跑道上P点水平向右跳出，初速度的方向与圆盘半径 $O M$ 在同一竖直平面内。已知圆盘的圆心与P点之间的水平距离为 $x_{0} = 4 m$ ，圆盘半径 $R = 2 m$ ，重力加速度g取 $10 m / s^{2}$ ，不计空气阻力.

(1)、求参赛者从P点跳出至落至圆盘经历的时间t；

(2)、参赛者要能落在圆盘上，求v₀的最小值；

(3)、若参赛者从P点跳出的同时，圆盘绕过其圆心O的竖直轴以角速度ω匀速转动，要使参赛者落到M点，求圆盘转动的角速度ω.

查看试题解析
14. 随着网络销售额的增长，很多快递公司采用传送带装置运送快递包裹，如图甲所示。为了调节运送装置，某公司设置图乙装置进行实验，现选用动摩擦因数 $μ = 0.5$ 的传送带， $A B$ 段水平，长度 $L_{A B} = 4 m$ ， $B C$ 段是倾斜的，长度 $L_{B C} = 5 m$ ，设置倾角为 $θ = 37 °$ ， $A B$ 和 $B C$ 在 $B$ 点通过一小段长度可忽略的圆弧连接，包裹通过圆弧时认为速度大小不改变（图中未画出圆弧），若传送带以 $v = 4 m / s$ 的恒定速率顺时针运转。现将一个包裹（可看作质点）无初速度放在A点进行试验，重力加速度 $g$ 取 $10 m / s^{2}$ 。（ $s i n 37 ° = 0.6$ ， $c o s 37 ° = 0.8$ ）则：

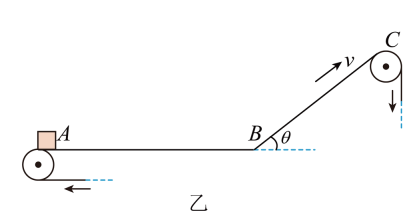(1)、包裹第一次到达 $B$ 点所用的时间；

(2)、包裹能否被运送到 $C$ 点，如果能请，计算 $B$ 到 $C$ 的时间，如果不能，计算包裹到达的最大高度？

查看试题解析
15. 2022年北京冬奥会上，中国花样滑冰队的隋文静、韩聪不负众望，在双人滑项目上强势夺冠，这也是中国队时隔12年之后再次登上奥运会最高领奖台。该项目有一项技术动作叫双人螺旋线，如图（a）所示，以男选手成为轴心，女选手围绕男选手旋转。将这一情景抽象成，如图（b）所示：一细线一端系住一小球，另一端固定在一竖直细杆上，小球以一定大小的速度随着细杆在水平面内做匀速圆周运动，细线便在空中划出一个圆锥面，这样的模型叫“圆锥摆”。圆锥摆是研究水平面内质点做匀速圆周运动动力学关系的典型特例。小球（可视为质点）质量为m，细线AC长度为L，重力加速度为g。

(1)、在紧贴着小球运动的水面上加一光滑平板，使球在板上做匀速圆周运动，此时细线与竖直方向所成夹角为θ，如图（c）所示，当小球的角速度ω大于某一值ω₁时，小球将脱离平板，则ω₁为多大？

(2)、撤去光滑平板，让小球在空中旋转，测试发现，当小球的角速度ω小于某一值ω₂时，细线会缠绕在竖直杆上，最后随细杆转动，如图（d）所示，则ω₂为多大？

(3)、在题（2）情境下，再用一根细线，同样一端系在该小球上，另一端固定在细杆上的B点，且当两条细线均伸直时，如图（e）所示，各部分长度之比 $| A B | ： | A C | ： | B C | = 5 ： 4 ： 3$ 。则当小球以 $ω^{'} = \sqrt{\frac{2 g}{\sqrt{3} L}}$ 匀速转动时，两细线的对小球的拉力分别多大？

查看试题解析