湖南省张家界市2023届高三下学期数学3月高考模拟试卷
试卷更新日期:2023-04-10 类型:高考模拟
一、单选题
-
1. 已知集合 , 集合.则( )A、 B、 C、 D、2. 已知复数 , 则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 有3本不同的科技类书,2本不同的文艺类书,若将其随机地并排摆放到书架的同一层上,则同一类别的书都不相邻的概率是( )A、 B、 C、 D、4. 已知是各项均为正数的等差数列,其公差为 , 若 , , 也是等差数列,则其公差为( )A、 B、 C、 D、5. 函数的部分图象大致形状是( )A、
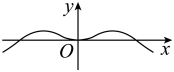 B、
B、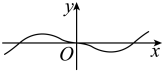 C、
C、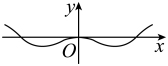 D、
D、 6. 将函数的图象绕原点逆时针旋转得到曲线 , 则曲线的标准方程是( )A、 B、 C、 D、7. 已知 , 且 , 则的取值范围是( )
6. 将函数的图象绕原点逆时针旋转得到曲线 , 则曲线的标准方程是( )A、 B、 C、 D、7. 已知 , 且 , 则的取值范围是( )(注:选项中的为自然对数的底数)
A、 B、 C、 D、8. 鲁班锁是我国传统的智力玩具,起源于中国古代建筑中的榫卯结构,其内部的凹凸部分啮合十分精巧.图1是一种鲁班锁玩具,图2是其直观图.它的表面由八个正三角形和六个正八边形构成,其中每条棱长均为2.若该玩具可以在一个正方体内任意转动(忽略摩擦),则此正方体表面积的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列命题正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 下列说法中正确的是( )A、一组数据11,12,12,13,14,15,16,18,20,22的第80百分位数为19 B、若随机变量 , 且 , 则 C、袋中装有除颜色外完全相同的4个红球和2个白球,从袋中不放回的依次抽取2个球.记事件{第一次抽到的是红球},事件{第二次抽到的是白球},则 D、已知变量x、y线性相关,由样本数据算得线性回归方程是 , 且由样本数据算得 , , 则11. 已知函数 , 则下列说法正确的有( )A、若 , 则 B、将的图象向左平移个单位长度后得到的图象关于轴对称 C、若在上有且仅有4个零点,则的取值范围为 D、是的导函数,令.则在上的值域为12. 过抛物线的焦点F的直线交抛物线E于A,B两点(点A在第一象限),M为线段AB的中点.若 , 则下列说法正确的是( )A、抛物线E的准线方程为 B、过A,B两点作抛物线的切线,两切线交于点N,则点N在以AB为直径的圆上 C、若为坐标原点,则 D、若过点且与直线垂直的直线交抛物线于C,D两点,则
三、填空题
-
13. 已知是单位向量, , 若向量与向量夹角 , 写出一个满足上述条件的向量.14. 已知为锐角, , 则 .15. 已知直线与圆心坐标为(为整数)且经过点的圆C相切,直线m:与圆C相交于A、B两点,则下列说法正确的是.
①圆C的标准方程为;
②若 , 则实数的值为2;
③若 , 则直线的方程为或;
④弦的中点M的轨迹方程为.
16. 已知函数的图像与直线:交于点 , , 其中 , 与直线:交于两点、 , 其中 , 则的最小值为.四、解答题
-
17. 数列中, , .(1)、求数列的通项公式;(2)、若 , 求数列的前项和.18. 记的三个内角A,B,C所对的边分别为a,b,c,.(1)、求A;(2)、若 , 求的面积的最大值.19. 如图,已知三棱柱 , , , 为线段上的动点,.
 (1)、求证:平面平面;(2)、若 , D为线段的中点, , 求与平面所成角的余弦值.20. 2022年底,新冠病毒肆虐全国,很多高三同学也都加入羊羊行列.某校参加某次大型考试时采用了线上考试和线下考试两种形式.现随机抽取200名同学的数学成绩做分析,其中线上人数占40%,线下人数占60%,通过分别统计他们的数学成绩得到了如下两个频率分部直方图:
(1)、求证:平面平面;(2)、若 , D为线段的中点, , 求与平面所成角的余弦值.20. 2022年底,新冠病毒肆虐全国,很多高三同学也都加入羊羊行列.某校参加某次大型考试时采用了线上考试和线下考试两种形式.现随机抽取200名同学的数学成绩做分析,其中线上人数占40%,线下人数占60%,通过分别统计他们的数学成绩得到了如下两个频率分部直方图:
其中称为合格,称为中等,称为良好,称为优秀,称为优异.
(1)、根据频率分布直方图,求这200名学生的数学平均分(同一组数据可取该组区间的中点值代替);(2)、现从这200名学生中随机抽取一名同学的数学成绩为良好,试分析他是来自线上考试的可能性大,还是来自线下考试的可能性大.(3)、现从线下考试的学生中随机抽取10名同学,且抽到k个学生的数学成绩为中等的可能性最大,试求k的值.