湖北省七市(州)2023届高三下学期数学3月联合统一调研测试试卷
试卷更新日期:2023-04-10 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则的元素个数为( )A、1 B、2 C、3 D、42. 若 , 则( )A、 B、 C、 D、3. 一组数据按照从小到大的顺序排列为1,2,3,5,6,8,记这组数据的上四分位数为n,则二项式展开式的常数项为( )A、-160 B、60 C、120 D、2404. 截角四面体是一种半正八面体,可由四面体经过适当的截角而得到.如图,将棱长为6的正四面体沿棱的三等分点作平行于底面的截面截角得到所有棱长均为2的截角四面体,则该截角四面体的体积为( )
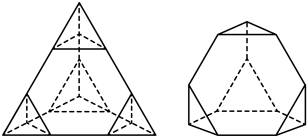 A、 B、 C、 D、5. 已知 , 则的值为( )A、 B、 C、 D、6. 已知 , , 直线与曲线相切,则的最小值是( )A、16 B、12 C、8 D、47. 已知 , 分别是双曲线的左、右焦点,过的直线分别交双曲线左、右两支于A,B两点,点C在x轴上, , 平分 , 则双曲线的离心率为( )A、 B、 C、 D、8. 已知函数 , 若成立,则实数a的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、5. 已知 , 则的值为( )A、 B、 C、 D、6. 已知 , , 直线与曲线相切,则的最小值是( )A、16 B、12 C、8 D、47. 已知 , 分别是双曲线的左、右焦点,过的直线分别交双曲线左、右两支于A,B两点,点C在x轴上, , 平分 , 则双曲线的离心率为( )A、 B、 C、 D、8. 已知函数 , 若成立,则实数a的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 下列命题中正确的是( )A、若样本数据 , , , 的样本方差为3,则数据 , , , 的方差为7 B、经验回归方程为时,变量x和y负相关 C、对于随机事件A与B, , , 若 , 则事件A与B相互独立 D、若 , 则取最大值时10. 已知函数的部分图象如图所示, , 则( )
 A、函数在上单调递减 B、函数在上的值域为 C、 D、曲线在处的切线斜率为11. 如图,在棱长为4的正方体中,E,F,G分别为棱 , , 的中点,点P为线段上的动点,则( )
A、函数在上单调递减 B、函数在上的值域为 C、 D、曲线在处的切线斜率为11. 如图,在棱长为4的正方体中,E,F,G分别为棱 , , 的中点,点P为线段上的动点,则( )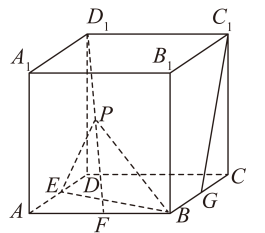 A、两条异面直线和所成的角为 B、存在点P,使得平面 C、对任意点P,平面平面 D、点到直线的距离为412. 已知直线交轴于点P,圆 , 过点P作圆M的两条切线,切点分别为A,B,直线与交于点C,则( )A、若直线l与圆M相切,则 B、当时,四边形的面积为 C、直线经过一定点 D、已知点 , 则为定值
A、两条异面直线和所成的角为 B、存在点P,使得平面 C、对任意点P,平面平面 D、点到直线的距离为412. 已知直线交轴于点P,圆 , 过点P作圆M的两条切线,切点分别为A,B,直线与交于点C,则( )A、若直线l与圆M相切,则 B、当时,四边形的面积为 C、直线经过一定点 D、已知点 , 则为定值三、填空题
-
13. 已知 , , 则在方向上的投影向量的坐标为 .14. 现有甲、乙两个口袋,其中甲口袋内装有三个1号球,两个2号球和一个3号球;乙口袋内装有两个1号球,一个2号球,一个3号球.第一次从甲口袋中任取1个球,将取出的球放入乙口袋中,第二次从乙口袋中任取一个球,则第二次取到2号球的概率为 .15. 函数 , 若关于x的不等式的解集为 , 则实数a的取值范围为 .16. 已知为抛物线上一点,过点的直线与抛物线C交于A,B两点,且直线与的倾斜角互补,则 .
四、解答题
-
17. 记的内角A,B,C的对边分别为a,b,c,已知 .(1)、求B;(2)、设 , 若点M是边上一点, , 且 , 求的面积.18. 设数列的前n项和为 . 已知 , , .(1)、求证:数列是等差数列;(2)、设数列的前n项和为 , 且 , 令 , 求数列的前n项和 .19. 某市举行招聘考试,共有4000人参加,分为初试和复试,初试通过后参加复试.为了解考生的考试情况,随机抽取了100名考生的初试成绩,并以此为样本绘制了样本频率分布直方图,如图所示.

附:若随机变量X服从正态分布 , 则: , , .
(1)、根据频率分布直方图,试求样本平均数的估计值;(2)、若所有考生的初试成绩X近似服从正态分布 , 其中为样本平均数的估计值, , 试估计初试成绩不低于88分的人数;(3)、复试共三道题,第一题考生答对得5分,答错得0分,后两题考生每答对一道题得10分,答错得0分,答完三道题后的得分之和为考生的复试成绩.已知某考生进入复试,他在复试中第一题答对的概率为 , 后两题答对的概率均为 , 且每道题回答正确与否互不影响.记该考生的复试成绩为Y,求Y的分布列及均值.20. 如图,在斜三棱柱中,底面是边长为2的正三角形,侧面为菱形,已知 , . (1)、当时,求三棱柱的体积;(2)、设点P为侧棱上一动点,当时,求直线与平面所成角的正弦值的取值范围.
(1)、当时,求三棱柱的体积;(2)、设点P为侧棱上一动点,当时,求直线与平面所成角的正弦值的取值范围.
