浙江省舟山市2023年中考数学一模试卷

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022年北京冬奥会3个赛区场馆使用绿色电力，减排320000吨二氧化碳．数字320000用科学记数法表示是（）

A、 $3.2 \times 10^{6}$ B、 $3.2 \times 10^{5}$ C、 $3.2 \times 10^{4}$ D、 $32 \times 10^{4}$

查看试题解析
2. 下列运算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(- 3 a b^{2})}^{2} = - 6 a^{2} b^{4}$ D、 $a \cdot a^{- 1} = 1 (a \neq 0)$

查看试题解析
3. 已知样本数据：3，2，1，7，2，下列说法不正确的是（）

A、平均数是3 B、中位数是1 C、众数是2 D、方差是4.4

查看试题解析
4. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“国”字所在面相对的面上的汉字是（）

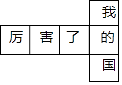A、厉 B、害 C、了 D、我

查看试题解析
5. 《九章算术》是中国古代的一部数学专著，其中记载了一道有趣的题：“今有凫起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日相逢？”大意是：今有野鸭从南海起飞，7天到北海；大雁从北海起飞，9天到南海.现野鸭从南海、大雁从北海同时起飞，问经过多少天相遇？设经过x天相遇，根据题意可列方程为（）

A、 $(\frac{1}{7} + \frac{1}{9}) x = 1$ B、 $(\frac{1}{7} - \frac{1}{9}) x = 1$ C、 $(9 - 7) x = 1$ D、 $(9 + 7) x = 1$

查看试题解析
6. 数形结合是解决数学问题常用的思想方法.如图，一次函数y＝kx+b（k、b为常数，且k＜0）的图象与直线y＝ $\frac{1}{3}$ x都经过点A（3，1），当kx+b＜ $\frac{1}{3}$ x时，x的取值范围是（）

A、x＞3 B、x＜3 C、x＜1 D、x＞1

查看试题解析
7. 如图，圆O是 $R t △ A B C$ 的外接圆， $∠ A C B = 90 °$ ， $∠ A = 25 °$ ，过点C作圆O的切线，交 $A B$ 的延长线于点D，则 $∠ D$ 的度数是（）

A、 $40 °$ B、 $50 °$ C、 $55 °$ D、 $65 °$

查看试题解析
8. 如图1，直线 $l_{1} ∥ l_{2}$ ，直线 $l_{3}$ 分别交直线 $l_{1}$ ， $l_{2}$ 于点A，B．小嘉在图1的基础上进行尺规作图，得到如图2，并探究得到下面两个结论：
①四边形ABCD是邻边不相等的平行四边形；②四边形ABCD是对角线互相垂直的平行四边形．下列判断正确的是（）

A、①②都正确 B、①错误，②正确 C、①②都错误 D、①正确，②错误

查看试题解析
9. 如图，已知正方形 $A B C D$ 的边长为4，E，F分别为 $A B$ ， $C D$ 边上的点，且 $E F ∥ B C$ ， G为 $E F$ 上一点，且 $G F = 1$ ， M，N分别为 $G D$ ， $E C$ 的中点，则 $M N$ 的长为（）

A、 $\frac{8}{3}$ B、 $\frac{9}{4}$ C、 $\frac{5}{2}$ D、 $\frac{12}{5}$

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + c$ 的图象与x轴的正半轴交于点 $A (p ， 0)$ ，点 $B (q ， 0)$ ；与y轴的正半轴交于点 $C (0 ， r)$ ，且 $p = r$ ， $q = 3 p$ ，那么b的值为（）

A、 $\frac{4}{3}$ B、 $- \frac{4}{3}$ C、 $\frac{3}{4}$ D、 $- \frac{3}{4}$

查看试题解析

二、填空题

11. 分解因式： $x y - y^{2} =$ ．

查看试题解析
12. 若一个正多边形的内角和等于外角和的两倍，则该正多边形的边数是 .

查看试题解析
13. 在网络课程学习中，小蕾和小丽分别在《好玩的数学》《美学欣赏》《人文中国》中随机选择一门，两人恰好选中同一门课程的概率为。

查看试题解析
14. 如图，在 $△ A B C$ 中，O是 $B C$ 的中点，以点O为位似中心，作 $△ A B C$ 的位似图形 $△ D E F$ .若点A的对应点D是 $△ A B C$ 的重心，则 $△ A B C$ 与 $△ D E F$ 的位似比为.

查看试题解析
15. 如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，其中点B的运动路径为 $\overset{⌢}{B B^{'}}$ ，则图中阴影部分的面积为.

查看试题解析
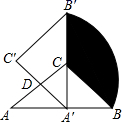16. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 8 c m$ ， $B C = 6 c m$ .动点P沿线段 $A C$ 以 $5 c m / s$ 的速度从点A向点C运动，另有一动点Q与点P同时出发，沿线段 $B C$ 以相同的速度从点B向点C运动.作 $P D ⊥ A B$ 于点D，再将 $△ A P D$ 绕 $P D$ 的中点旋转 $180 °$ ，得到 $△ A^{'} D P$ ；作 $Q E ⊥ A B$ 于点E，再将 $△ B Q E$ 绕 $Q E$ 的中点旋转 $180 °$ ，得到 $△ B^{'} E Q$ .设点P的运动时间为 $x s$ .

(1)、如图当点 $A^{'}$ 落在 $B C$ 边上时x的值为；

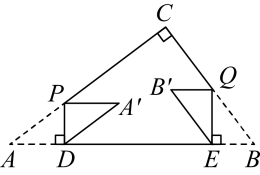(2)、如图，在点P，Q运动中：当点 $A^{'}$ 在 $△ B^{'} E Q$ 内部时x的取值范围为.

查看试题解析

三、解答题

17.

(1)、计算： $| - 2 | + {(\sqrt{3} - 2)}^{0} + t a n 45 °$ ；

(2)、解不等式： $2 x - 3 (x + 1) ≥ 1$

查看试题解析
18. 在学习一元二次方程的根与系数关系一课时老师出示了这样一个题目：已知关于x的方程 $x^{2} - (2 m - 1) x + m^{2} = 0$ 的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $(x_{1} + 1) (x_{2} + 1) = 3$ ，求m的值.
波波同学的解答过程如框：
解：
由题意可知： ${\begin{array}{l} x_{1} + x_{2} = 2 m - 1 \\ x_{1} \cdot x_{2} = m^{2} \end{array}$
∵ $(x_{1} + 1) (x_{2} + 1) = x_{1} \cdot x_{2} + x_{1} + x_{2} + 1 = 3$ ，
∴ $m^{2} + (2 m - 1) + 1 = 3$ ，
解得： $m = - 3$ 或 $m = 1$
波波的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程.

查看试题解析
19. 观察下列各式：① $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， ② $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ；③ $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ， …

(1)、请观察规律，并写出第④个等式：；

(2)、请用含n（n≥1）的式子写出你猜想的规律：；

(3)、请证明（2）中的结论.

查看试题解析
20. 某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2022年初的视力数据，并调取该批学生2021年初的视力数据，制成如下统计图（不完整）：
青少年视力健康标准
类别
视力
健康状况
A
视力 $≥ 5.0$
视力正常
B
视力 $= 4.9$
轻度视力不良
C
$4.6 ≤$ 视力 $≤ 4.8$
中度视力不良
D
视力 $≤ 4.5$
重度视力不良
根据以上信息，请解答：

(1)、分别求出被抽查的400名学生2021年初视力正常（类别A）的人数和2022年初轻度视力不良（类别B）的扇形圆心角度数.

(2)、若2022年初该市有八年级学生8000人，请估计这些学生2022年初视力正常的人数比2021年初增加了多少人？

(3)、国家卫健委要求，全国初中生视力不良率控制在69%以内.请估计该市八年级学生2022年初视力不良率是否符合要求？并说明理由.

查看试题解析
21. 如图1是一种可折叠的台灯，图2是台灯的结构图， $A C$ 是可以绕点A旋转的支架，点C为灯泡的位置，灯罩可绕点C旋转.量得 $A B = 10 c m$ ， $A C = 20 c m$ ，此时 $∠ A B F = 37 °$ ，且 $C E ⊥ D E$ .

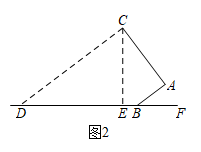(1)、当 $∠ A = 90 °$ ， $C D ⊥ A C$ 时（图2），求灯泡C所在的高度；

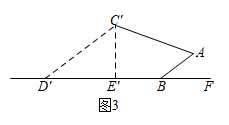(2)、在（1）的条件下，旋转支架 $A C$ （ $A B$ 固定）.当 $∠ A$ 从 $90 °$ 变成 $57 °$ （图3）时，且 $∠ D^{'} C^{'} E^{'}$ 的度数不变， $C^{'} E^{'} ⊥ D^{'} E^{'}$ ，求 $D E - D^{'} E^{'}$ 的值.（结果精确到0.1，参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $s i n 20 ° \approx 0.34$ ， $c o s 20 ° \approx 0.94$ ， $t a n 20 ° \approx 0.36$ ）

查看试题解析
22. 已知A是反比例函数 $y = \frac{2}{x}$ （ $x > 0$ ）图象上一个动点，过点A作x轴的平行线，交直线 $y = - 2 x$ 于点B，以线段 $A B$ 为一条对角线，作 $▱ O A C B$ （O为坐标原点）.

(1)、如图，当点C在y轴上时，请证明 $▱ O A C B$ 是菱形，并求点C的坐标；

(2)、如图，当 $▱ O A C B$ 是矩形时，求点B，C的坐标.

查看试题解析
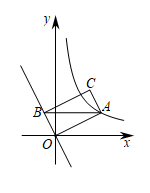23. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ .

(1)、若 $a = - 1$ ，且函数图象经过 $(0 ， 3)$ ， $(2 ， - 5)$ 两点，求此二次函数的解析式；并根据图象直接写出函数值 $y \geq 3$ 时自变量x的取值范围；

(2)、在（1）的条件下，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A，B两点（点A在点B的左侧），将这条抛物线向右平移m（ $m > 0$ ）个单位，平移后的抛物线于x轴交于C，D两点（点C在点D的左侧），若B，C是线段 $A D$ 的三等分点，求m的值.

(3)、已知 $a = b = c = 1$ ，当 $x = p$ ， q（p，q是实数， $p \neq q$ ）时，该函数对应的函数值分别为P，Q.若 $p + q = 2$ ，求证 $P + Q > 6$ .

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ A B C$ 的平分线交 $A C$ 于点E，以A为圆心， $A E$ 为半径作 $⊙ A$ 交 $B E$ 于点F，直线 $A B$ 交 $⊙ A$ 于G、H两点， $A F$ 的延长线交 $B C$ 于点D，作 $E K ⊥ B C$ ，垂足为点K.

(1)、求证： $A D ⊥ B C$ ；

(2)、求证： $\frac{B F}{B E} = \frac{A D}{A C}$ ；

(3)、当 $B F \cdot B E = B G \cdot B H$ 且 $A H = B D$ 时，求证： $\frac{B F}{B G} = \frac{A C}{B E}$ .

查看试题解析

类别	视力	健康状况
A	视力 $≥ 5.0$	视力正常
B	视力 $= 4.9$	轻度视力不良
C	$4.6 ≤$ 视力 $≤ 4.8$	中度视力不良
D	视力 $≤ 4.5$	重度视力不良