浙江省温州市瑞安市2023年初中学业水平第一次适应性测试数学试题

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 相反数的是（）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
2. 2022年5月，中国墨子号卫星实现1200000米地表量子态传输新纪录.数据1200000用科学记数法表示为（）

A、 $120 \times 1 0^{4}$ B、 $12 \times 1 0^{5}$ C、 $1.2 \times 1 0^{6}$ D、 $0.12 \times 1 0^{7}$

查看试题解析
3. 某物体如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 若分式 $\frac{2 x + 4}{x - 3}$ 的值为0，则x的值是（）

A、 $2$ B、 $1$ C、 $0$ D、 $- 2$

查看试题解析
5. 某校参加数学节的学生人数统计图如图所示，若参加说题比赛的学生有60人，则参加解题比赛有（）

A、70人 B、75人 C、80人 D、85人

查看试题解析
6. 化简 $2 a^{3} \div (- a)$ 的结果是（）

A、 $2 a^{2}$ B、 $- 2 a^{2}$ C、2a D、－2a

查看试题解析
7. 如图，在 $△ A B C$ 中，点D，E分别是 $A C ， B C$ 的中点，以点A为圆心， $A D$ 为半径作圆弧交 $A B$ 于点F.若 $A D = 7$ ， $D E = 5$ ，则 $B F$ 的长为（）

A、2 B、2.5 C、3 D、3.5

查看试题解析
8. 某路灯示意图如图所示，它是轴对称图形.若 $∠ A C B = 130 °$ ， $A C = B C = 1.2 m$ ， $C D$ 与地面垂直且 $C D = 3 m$ ，则灯顶A到地面的高度为（）m

A、 $3 + 1.2 c o s 25 °$ B、 $3 + 1.2 s i n 25 °$ C、 $3 + \frac{1.2}{c o s 25 °}$ D、 $3 + \frac{1.2}{s i n 25 °}$

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ， a，b，c为常数）的部分对应值列表如下：
x
…
－1
0
1
2
…
y
…
$c + 6$
c
$c - 2$
c
…
则代数式 $9 a + 3 b$ 的值为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，以其三边为边向外作正方形，连接 $E H$ ，交 $A C$ 于点P，过点P作 $P R ⊥ F G$ 于点R.若 $t a n ∠ A H E = \frac{1}{2}$ ， $E H = 8 \sqrt{5}$ ，则 $P R$ 的值为（）

A、10 B、11 C、 $4 \sqrt{5}$ D、 $5 \sqrt{5}$

查看试题解析

二、填空题

11. 分解因式： $a^{2} - 49 =$ ．

查看试题解析
12. 在一个不透明的袋中装有9个只有颜色不同的球，其中5个红球，3个黄球，1个白球，从袋中任意摸出一个球是红球的概率为.

查看试题解析
13. 若扇形的圆心角为36°，半径为15，则该扇形的弧长为.

查看试题解析
14. 不等式组 ${\begin{array}{l} x - 6 \geq 2 \\ \frac{x + 1}{2} > 3 \end{array}$ 的解集为.

查看试题解析
15. 如图，直线 $y = - \sqrt{3} x + 3$ 分别交x轴，y轴于点A，B，将 $△ A O B$ 绕点O逆时针旋转至 $△ C O D$ ，使点C落在 $A B$ 上， $C D$ 交y轴于点E.分别记 $△ B C E$ ， $△ D E O$ 的面积为 $S_{1}$ ， $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值为.

查看试题解析
16. 如图，某公园有一月牙形水池，水池边缘有A，B，C，D，E五盏装饰灯.为了估测该水池的大小，观测员在A，D两点处发现点A，E，C和D，E，B均在同一直线上，沿AD方向走到F点，发现 $∠ A F C = 90 °$ .测得 $A D = 9.6$ 米， $A E = D E = 8$ 米， $D F = 2.4$ 米，则 $\overset{⌢}{A E D}$ 所在圆的半径为米， $\overset{⌢}{A B C}$ 所在圆的半径为米.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{9} - | - 5 | + {(\sqrt{5})}^{0} - (- 2)$ .

(2)、 $\frac{a^{2} + 3 a b}{a b} - \frac{a (a + b)}{a b}$ .

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D为 $△ A B C$ 内一点，且 $A D$ 平分 $∠ B A C$ .

(1)、求证： $△ A B D ≅ △ A C D$ .

(2)、若 $A B = B C$ ， $∠ D B C = 40 °$ ，求 $∠ A C D$ 的度数.

查看试题解析
19. 某校进行安全知识测试.测试成绩分为A，B，C，D四个等级，依次记为10分，9分，8分，7分.学校随机抽取了20名女生和20名男生的成绩进行整理，得到了如下信息：
统计量
平均数
中位数
众数
女生
▲
8
7
男生
8.4
▲
9

(1)、求此次测试中，被抽查女生的平均成绩和男生成绩的中位数.

(2)、根据上面表格中的三组统计量，你认为男生、女生谁的成绩较好？请简述理由.

查看试题解析
20. 如图， $5 \times 5$ 网格是由边长为 $1$ 个单位的小菱形组成，每个菱形较小的角都是 $60 °$ .已知格点P，请按以下要求画格点图形（顶点都在格点上）.

(1)、在图1中画一个 $△ P A B$ ，使 $∠ A P B = 120 °$ ， $P A = 2$ ，再画出该三角形向右平移 $2$ 个单位后的图形.

(2)、在图2中画一个 $R t △ P C D$ ，使 $∠ C P D = 90 °$ ，且该三角形的面积为 $\sqrt{3}$ .注：图1，图2在答题纸上.

查看试题解析
21. 如图，直线 $y = 2 x$ 与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于A，B两点，点A的横坐标为2.

(1)、求这个反比例函数的表达式.

(2)、若点P在反比例函数图象上，且在直线 $A B$ 的下方（不与点A，B重合），求点P横坐标的取值范围.

查看试题解析
22. 如图， $A B$ 是半圆O的直径， $\overset{⌢}{A C} = \overset{⌢}{B C}$ ，在 $A B$ 的延长线上取点D，连接 $D C$ 并延长交半圆O的切线 $A E$ 于点E.过点A作 $A F ∥ E D$ ，交 $C O$ 的延长线于点F.

(1)、求证：四边形 $A E C F$ 是平行四边形.

(2)、若 $D C ： D E = 3 ： 5$ ， $A F = \sqrt{13}$ ，求 $A E$ 的长.

查看试题解析

23. 根据以下素材，探索完成任务.

如何设计喷水装置的高度？
素材1	图1为某公园的圆形喷水池，图2是其示意图，O为水池中心，喷头A、B之间的距离为20米，喷射水柱呈抛物线形，水柱距水池中心 $7 m$ 处达到最高，高度为 $5 m$ .水池中心处有一个圆柱形蓄水池，其底面直径 $C D$ 为 $12 m$ ，高 $C F$ 为1.8米.
素材1
素材2	如图3，拟在圆柱形蓄水池中心处建一喷水装置 $O P$ （ $O P ⊥ C D$ ，并从点P向四周喷射与图2中形状相同的抛物线形水柱，且满足以下条件： ①水柱的最高点与点P的高度差为 $0.8 m$ ； ②不能碰到图2中的水柱； ③落水点G，M的间距满足： $G M ： F M = 2 ： 7$ .
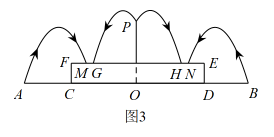
问题解决
任务1	确定水柱形状	在图2中以点O为坐标原点，水平方向为x轴建立直角坐标系，并求左边这条抛物线的函数表达式.
任务2	探究落水点位置	在建立的坐标系中，求落水点G的坐标.
任务3	拟定喷水装置的高度	求出喷水装置 $O P$ 的高度.

查看试题解析

24. 如图，在矩形 $A B C D$ 中， $A D = 3$ ，点E在 $A B$ 上， $A E = 1$ ， $C E = C D$ ， $D F ⊥ C E$ 于点 $F ， M ， N$ 分别是线段 $C B ， C F$ 上的点，且满足 $\frac{C M}{F N} = \frac{5}{3}$ ，设 $C M = x$ ， $E N = y$ .

(1)、求 $C E$ 的长.

(2)、求y关于x的函数表达式.

(3)、连结 $M N$ ，过点M作 $M H ∥ C E$ 交 $A B$ 于点H，连结 $N H$ .
①在 $△ N H M$ 中，以 $H M$ 为一边的角等于 $∠ A D F$ 时，求y的值.
②作点H关于 $M N$ 的对称点 $H^{'}$ ，当点H落在边 $B C$ 上时，求 $\frac{C H'}{B H'}$ 的值.

查看试题解析

x	…	－1	0	1	2	…
y	…	$c + 6$	c	$c - 2$	c	…

统计量	平均数	中位数	众数
女生	▲	8	7
男生	8.4	▲	9