浙江省金华市婺城区2023年九年级下学期联考数学试卷

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 小张抛一枚质地均匀的硬币，出现正面朝上的可能性是（　　）

A、25% B、50% C、75% D、85%

查看试题解析
2. 下列立体图形中，左视图与主视图不同的是（）

A、正方体 B、圆柱 C、圆锥 D、球

查看试题解析
3. 下列各组数中，成比例的是（）.

A、1， $- 2$ ， $- 3$ ， $- 6$ B、1，4，2， $- 8$ C、5，6，2，3 D、 $\sqrt{2}$ ， $\sqrt{6}$ ， 1， $\sqrt{3}$

查看试题解析
4. 将抛物线 $y = 4 x^{2}$ 向上平移3个单位后所得的抛物线解析式是（）.

A、 $y = 4 x^{2} + 3$ B、 $y = 4 x^{2} - 3$ C、 $y = 4 {(x + 3)}^{2}$ D、 $y = 4 {(x - 3)}^{2}$

查看试题解析
5.
正方形网格中，∠AOB如图放置，则sin∠AOB=（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{1}{2}$ D、2

查看试题解析
6. 抛一个铁球，在泥地上砸了一个直径 $8 c m$ ，深 $2 c m$ 的坑，这个铁球的直径是（）

A、 $12 c m$ B、 $10 c m$ C、 $8 \sqrt{2} c m$ D、 $6 \sqrt{3} c m$

查看试题解析
7. 如果一个扇形的半径是2，弧长是 $\frac{π}{2}$ ，则此扇形的圆心角的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
8. 关于抛物线 $y = - x^{2} + 2 x - 3$ 的判断，下列说法正确的是（）.

A、抛物线的开口方向向上 B、抛物线的对称轴是直线 $x = - 1$ C、在抛物线对称轴左侧，y随x增大而减小 D、抛物线顶点到x轴的距离是2

查看试题解析
9. 如图，△ABC是一张周长为18cm的三角形纸片，BC=5cm，⊙O是它的内切圆，小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（）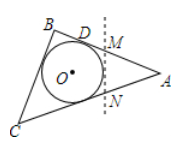

A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化

查看试题解析
10. 如图1是一座立交桥的示意图（道路宽度忽略不计），A为入口，F，G为出口，其中直行道为AB，CG，EF，且AB＝CG＝EF；弯道为以点O为圆心的一段弧，且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥，均以8m/s的速度行驶，从不同出口驶出，其间两车到点O的距离y（m）与时间x（s）的对应关系如图2所示，结合题目信息，下列说法错误的是（）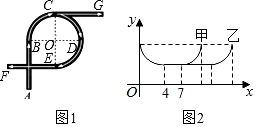

A、立交桥总长为168 m B、从F口出比从G口出多行驶48m C、甲车在立交桥上共行驶11 s D、甲车从F口出，乙车从G口出

查看试题解析

二、填空题

11. 请你写出一个顶点在 $x$ 轴上的二次函数表达式.

查看试题解析
12. 一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在岔路口随机选择一条路径，它获得食物的概率是。

查看试题解析
13. 已知C是线段AB的黄金分割点， $A C > B C$ ，若 $A B = 2$ ，则 $A C$ 的长为.（结果保留根号）

查看试题解析
14. 如图，矩形ABCD中，AB＝2，BC＝4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为.

查看试题解析
15. 一个滑轮起重装置如图所示，滑轮的半径是10cm，当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时，重物上升 cm（结果保留π）．

查看试题解析
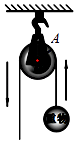16. 如图1是超市的手推车，如图2是其侧面示意图，已知前后车轮半径均为 $5 c m$ ，两个车轮的圆心的连线 $A B$ 与地面平行，测得支架 $A C = B C = 60 c m$ ， $A C$ 、 $C D$ 所在直线与地面的夹角分别为 $30 °$ 、 $60 °$ ， $C D = 50 c m$ .

(1)、扶手前端D到地面的距离为；

(2)、手推车内装有简易宝宝椅， $E F$ 为小坐板，打开后，椅子的支点H到点C的距离为10cm， $D F = 20 c m$ ， $E F ∥ A B$ ， $∠ E H D = 45 °$ ，坐板 $E F$ 的宽度为.

查看试题解析

三、解答题

17. 计算： $s i n 30 ° + c o s 60 ° - \sqrt{2} c o s 45 °$ .

查看试题解析

四、填空题

18. 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C，AB=6，AD=4，求线段CD的长.

查看试题解析

五、解答题

19. 如图1，一扇窗户打开一定角度，其中一端固定在窗户边OM上的点A处，另一端B在边ON上滑动，图2为某一位置从上往下看的平面图，测得∠ABO为37°，∠AOB为45°，OB长为35厘米，求AB的长（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
20. 在一个不透明袋子中有1个红球、1 个绿球和n个白球，这些球除颜色外都相同．

(1)、从袋中随机摸出1个球，记录下颜色后放回袋子中并搅匀，不断重复该试验．发现摸到白球的频率稳定在0.75，则n的值为；

(2)、当n=2时，把袋中的球搅匀后任意摸出2个球，求摸出的2个球颜色不同的概率．

查看试题解析
21. 如图，AB是⊙O的直径，C是 $\overset{⌢}{B D}$ 的中点，CE⊥AB于 E，BD交CE于点F.

(1)、求证：CF﹦BF；

(2)、若CD﹦6， AC﹦8，则⊙O的半径和CE的长.

查看试题解析
22. 规定：在平面内，如果一个图形绕一个定点旋转一定的角度α（0°＜α≤180°）后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角度α称为这个图形的一个旋转角.例如：正方形绕着两条对角线的交点O旋转90°或180°后，能与自身重合（如图1），所以正方形是旋转对称图形，且有两个旋转角.

根据以上规定，回答问题：

(1)、下列图形是旋转对称图形，但不是中心对称图形的是________；

A、矩形 B、正五边形 C、菱形 D、正六边形

(2)、下列图形中，是旋转对称图形，且有一个旋转角是60度的有：（填序号）；

(3)、下列三个命题：①中心对称图形是旋转对称图形；②等腰三角形是旋转对称图形；③圆是旋转对称图形，其中真命题的个数有（）个；

A、0 B、1 C、2 D、3

(4)、如图2的旋转对称图形由等腰直角三角形和圆构成，旋转角有45°，90°，135°，180°，将图形补充完整.

查看试题解析
23. 如图所示，△ABC为Rt△，∠ACB＝90°，点D为AB的中点，点E为边AC上的点，连结DE，过点E作EF⊥ED交BC于F，以DE，EF为邻边作矩形DEFG，已知AC＝8.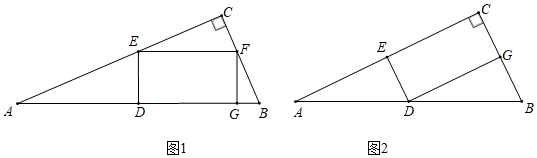

(1)、如图1所示，当BC＝6，点G在边AB上时，求DE的长.

(2)、如图2所示，若 $\frac{D E}{E F} = \frac{1}{2}$ ，点G在边BC上时，求BC的长.

(3)、①若 $\frac{D E}{E F} = \frac{1}{4}$ ，且点G恰好落在Rt△ABC的边上，求BC的长.
②若 $\frac{D E}{E F} = \frac{1}{2 n}$ （n为正整数），且点G恰好落在Rt△ABC的边上，请直接写出BC的长.

查看试题解析
24. 如图，直线 $y = \frac{3}{2} x + 3$ 与x轴、y轴交于点A、C，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 经过点A、C，与x轴的另一个交点是B，点P是直线 $A C$ 上的一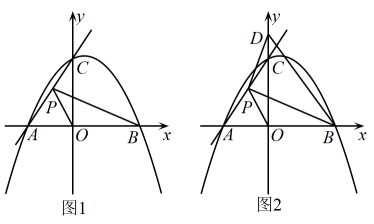动点.

(1)、求抛物线的解析式和点B的坐标；

(2)、如图1，求当 $O P + P B$ 的值最小时点P的坐标；

(3)、如图2，过点P作 $P B$ 的垂线交y轴于点D，是否存在点P，使以P、D、B为顶点的三角形与 $△ A O C$ 相似？若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析