浙江省杭州市2023年中考数学模拟卷

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $- 4 \div 2$ 的结果是（）.

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 第四届世界茉莉花大会、2022年中国（横州）茉莉花文化节于9月19日、20日在南宁市和横州市两地举行，茉莉花产业成了横州市一张靓丽的名片，目前横州市茉莉花种植面积约125000亩.数据125000用科学记数法可表示为（）

A、 $0.125 \times 1 0^{6}$ B、 $1.25 \times 1 0^{5}$ C、 $12.5 \times 1 0^{4}$ D、 $125 \times 1 0^{3}$

查看试题解析
3. 计算 $a^{6} \cdot a^{2}$ 的结果是（）

A、 $a^{3}$ B、 $a^{4}$ C、 $a^{8}$ D、 $a^{12}$

查看试题解析
4. 在平面直角坐标系中，点 $P (- 1 ， 2)$ 关于原点对称的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 祖冲之是中国数学史上第一个名列正史的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献．数学活动课上，孙老师对圆周率的小数点后100位数字进行了统计：
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14
那么，圆周率的小数点后100位数字的众数与中位数分别为（）

A、14，5 B、5，9 C、9，5 D、14，4.5

查看试题解析
6. 从甲、乙、丙、丁四名青年骨干教师中随机选取两名去参加“同心向党”演讲比赛，则恰好抽到甲、丙两人的概率是 $($ $)$

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 如果关于x的一元二次方程 $a x^{2} + b x + 1 = 0$ 的一个解是x＝1，则代数式2022－a－b的值为（）

A、－2022 B、2021 C、2022 D、2023

查看试题解析
8. 若一个多边形的每一个内角都等于 $140 °$ ，则这个多边形的边数是（）

A、7 B、8 C、9 D、10

查看试题解析
9. 某活动小组购买了4个篮球和5个足球，一共花费435元，其中篮球的单价比足球的单价多3元，求篮球的单价和足球的单价.设篮球的单价为 $x$ 元，足球的单价为 $y$ 元，依题意可列方程组为（）

A、 ${\begin{array}{l} x - y = 3 \\ 4 y + 3 y = 435 \end{array}$ B、 ${\begin{array}{l} y - x = 3 \\ 4 x + 5 y = 435 \end{array}$ C、 ${\begin{array}{l} x = 3 - y \\ 4 x + 5 y = 435 \end{array}$ D、 ${\begin{array}{l} x - y = 3 \\ 4 x + 5 y = 435 \end{array}$

查看试题解析
10. 已知在平面直角坐标系 $x O y$ 中，过点O的直线交反比例函数 $y = \frac{1}{x}$ 的图象于A，B两点（点A在第一象限），过点A作 $A C ⊥ x$ 轴于点C，连结 $B C$ 并延长，交反比例函数图象于点D，连结 $A D$ ，将 $△ A C B$ 沿线段 $A C$ 所在的直线翻折，得到 $△ A C B_{1}$ ， $A B_{1}$ 与 $C D$ 交于点E.若点D的横坐标为2，则 $A E$ 的长是（）

A、 $\frac{2}{3}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析

二、填空题

11. 分解因式： $x^{2} - 9 y^{2} =$

查看试题解析
12. 五线谱是一种记谱法，通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图， $A$ ， $B$ ， $C$ 为直线 $l$ 与五线谱的横线相交的三个点，则 $\frac{A B}{B C}$ 的值是.

查看试题解析
13. 不等式组 ${\begin{array}{l} x + 3 < 4 \\ \frac{2 - x}{4} \leq 1 \end{array}$ 的解为.

查看试题解析
14. 如图，一辆小车沿倾斜角为 $α$ 的斜坡向上行驶26米，已知 $c o s α = \frac{12}{13}$ ，则小车上升的高度是米.

查看试题解析
15. 如图，以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点，交直角边AC于点E．B、E是半圆弧的三等分点，弧BE的长为 $\frac{2 π}{3}$ ，则图中阴影部分的面积为．

查看试题解析
16. 如图，菱形 $O A B C$ 的一边 $O A$ 在 $x$ 轴的负半轴上，O是坐标原点，A点坐标为 $(- 5 ， 0)$ ，对角线 $A C$ 和 $O B$ 相交于点D且 $A C \cdot O B = 40$ .若反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象经过点D，并与 $B C$ 的延长线交于点E，则 $S_{△ O C E} =$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $| - 5 | + \sqrt{25} - {(2020 - \sqrt{3})}^{0}$ ；

(2)、x（1－x）+（x+1）（x－1）．

查看试题解析
18. 某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

(1)、在这次调查中，喜欢篮球项目的同学有人，在扇形统计图中，“乒乓球”的百分比为 %，如果学校有800名学生，估计全校学生中有人喜欢篮球项目．

(2)、请将条形统计图补充完整．

(3)、在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．

查看试题解析
19. 已知，如图，点A，D，B，E在同一条直线上， $A C = E F ， A D = E B ， ∠ A = ∠ E$ ， $B C$ 与 $D F$ 交于点G.

(1)、求证： $△ A B C ≌ △ E D F$ ；

(2)、当 $∠ C G D = 110 °$ 时，求 $∠ G B D$ 的度数.

查看试题解析
20. 如图， $△ A B C$ 内接于 $⊙ O$ ， $A B = A C$ ， $△ A D C$ 与 $△ A B C$ 关于直线 $A C$ 对称， $A D$ 交 $⊙ O$ 于点E.

(1)、求证： $C D$ 是 $⊙ O$ 的切线.

(2)、连接 $C E$ ，若 $c o s D = \frac{1}{3}$ ， $A B = 6$ ，求 $C E$ 的长.

查看试题解析
21. 小李、小王分别从甲地出发，骑自行车沿同一条路到乙地参加公益活动.如图，折线 $O A B$ 和线段 $C D$ 分别表示小李、小王离甲地的距离y（单位：千米）与时间x（单位：小时）之间的函数关系.根据图中提供的信息，解答下列问题：

(1)、求小王的骑车速度，点C的横坐标；

(2)、求线段 $A B$ 对应的函数表达式；

(3)、当小王到达乙地时，小李距乙地还有多远？

查看试题解析
22. 如图，在正方形ABCD中， $A B = 6$ ， E为AB的中点，连接CE，作 $C F ⊥ E C$ 交射线AD于点F，过点F作 $F G ∥ C E$ 交射线CD于点G，连接EG交AD于点H.

(1)、求证： $C E = C F$ .

(2)、求HD的长.

(3)、如图2，连接CH，点P为CE的中点，Q为AF上一动点，连接PQ，当 $∠ Q P C$ 与四边形GHCF中的一个内角相等时，求所有满足条件的DQ的长.

查看试题解析
23. 如图1，抛物线 $y = \frac{1}{2} x^{2} + b x + c (c < 0)$ 与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，过点C作 $C D ∥ x$ 轴，与抛物线交于另一点D，直线 $B C$ 与 $A D$ 相交于点M.

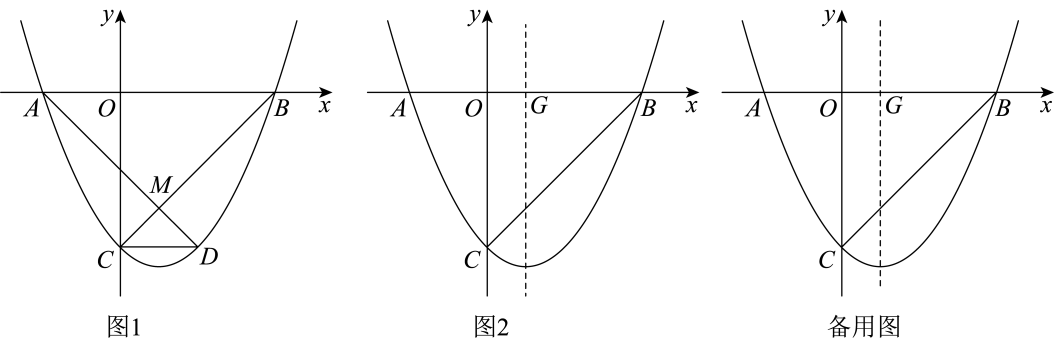(1)、已知点C的坐标是 $(0 ， - 4)$ ，点B的坐标是 $(4 ， 0)$ ，求此抛物线的解析式；

(2)、若 $b = \frac{1}{2} c + 1$ ，求证： $A D ⊥ B C$ ；

(3)、如图2，设第（1）题中抛物线的对称轴与x轴交于点G，点P是抛物线上在对称轴右侧部分的一点，点P的横坐标为t，点Q是直线 $B C$ 上一点，是否存在这样的点P，使得 $△ P G Q$ 是以点G为直角顶点的直角三角形，且满足 $∠ G Q P = ∠ O C A$ ，若存在，请直接写出t的值；若不存在，请说明理由.

查看试题解析

数字	0	1	2	3	4	5	6	7	8	9
频数	8	8	12	11	10	8	9	8	12	14