陕西省宝鸡市陈仓区2023年中考数学一模试卷

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1.
如图是一个几何体的俯视图，则该几何体可能是（　　）

A、 B、 C、 D、

查看试题解析
2. 已知点P（-2，3）是反比例函数y= $\frac{k}{x}$ 图象上的一点，则下列各点中，也在该函数图象上的是（）

A、（2，-3） B、（3，2） C、（-2，-3） D、（2，3）

查看试题解析
3. 方程x²﹣2x+3=0的根的情况是（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有一个实数根

查看试题解析
4. 点 $A (3 ， n)$ 关于y轴对称点的坐标为 $(- 3 ， 2)$ ，那么点A关于原点对称点的坐标是（）

A、 $(- 3 ， 2)$ B、 $(- 3 ， - 2)$ C、 $(2 ， - 3)$ D、 $(2 ， 3)$

查看试题解析
5. 下列函数中，y随x的增大而减少的是（）.

A、 $y = \frac{1}{x}$ B、 $y = \frac{2}{x}$ C、 $y = - \frac{3}{x} (x > 0)$ D、 $y = \frac{4}{x} (x < 0)$

查看试题解析
6. 如图， $⊙ O$ 的直径 $C D = 10 c m$ ， $A B$ 是 $⊙ O$ 的弦， $A B ⊥ C D$ ，垂足为M， $O M = 3 c m$ ，则 $A B$ 的长为（）

A、 $4 c m$ B、 $6 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
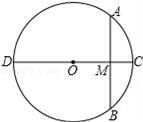7. 如图，四边形ABCD是正方形，△ADE绕着点A旋转90°后到达△ABF的位置，连接EF，则△AEF的形状是（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
8. 已知 $\frac{b}{a} = \frac{5}{13}$ ，则 $\frac{a + b}{a - b}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{9}{4}$ D、 $\frac{4}{9}$

查看试题解析
9. 某公司今年10月的营业额为2000万元，按计划第四季度的总营业额为7980万元.若该公司11、12两个月营业额的月均增长率均为x，依题意可列方程为（）

A、2000 ${(1 + x)}^{2}$ ＝7980 B、2000 ${(1 + x)}^{3}$ ＝7980 C、2000(1+3x)＝7980 D、2000+2000(1+x)+2000 ${(1 + x)}^{2}$ ＝7980

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图，其对称轴为直线 $x = 1$ ，给出下列结论：① $b^{2} - 4 a c > 0$ ；② $2 a + b = 0$ ；③ $a b c > 0$ ；④ $3 a + c > 0$ ，则正确的结论个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知双曲线 $y = \frac{k}{x}$ 经过点（2，-3），则k的值是.

查看试题解析
12. 等腰 $△ A B C$ 一腰上的高为 $\sqrt{3}$ ，这条高与底边的夹角为 $60 °$ ，则 $△ A B C$ 的面积是.

查看试题解析
13. 二次函数 $y = 2 x^{2} - 4 x - 3$ 图象的对称轴为.

查看试题解析
14. 如图，在平面直角坐标系 $x O y$ 中， $R t △ O C D$ 的一边 $O C$ 在x轴上， $∠ O C D = 90 °$ ，点D在第一象限， $O C = 6 ， D C = 8$ ，反比例函数 $y = \frac{k}{x}$ 的图象经过 $O D$ 的中点A，则k=.

查看试题解析
15. 如图，弧AB所对圆心角∠AOB＝90°，半径为4，点C是OB中点，点D是弧AB上一点，CD绕点C逆时针旋转90°得到CE，则AE的最小值是.

查看试题解析

三、解答题

16. 计算： $(4 - \sqrt{3})^{0} - 3 t a n 60 ° - (- \frac{1}{2})^{- 1} + \sqrt{2}$ ．

查看试题解析
17. 解方程： $x^{2} - 4 x - 12 = 0$ .

查看试题解析
18. 某校举行以“助人为乐，乐在其中”为主题的演讲比赛，比赛设一个第一名，一个第二名，两个并列第三名.前四名中七，八年各有一名同学，九年级有两名同学，小蒙同学认为前两名是九年级同学的概率是 $\frac{1}{2}$ ，你赞成他的观点吗？请用列表法或画树形图法分析说明.

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D为边BC上一点，以AB，BD为邻边作 $▱ A B D E$ ，连接AD、EC.

(1)、求证： $△ A D C ≌ △ E C D$ ；

(2)、若 $B D = C D$ ，求证：四边形ADCE是矩形.

查看试题解析
20. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{m}{x}$ 图象交于A，B两点，与x轴交于点C $(- 2 ， 0)$ ，点A的横坐标为1， $S_{△ A O C} = 2$ .

(1)、求一次函数及反比例函数的表达式；

(2)、直接写出反比例函数值大于一次函数值时x的取值范围.

查看试题解析
21. 定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形.
根据以上定义，解决下列问题：

(1)、如图1，正方形ABCD中E是CD上的点，将△BCE绕B点旋转，使BC与BA重合，此时点E的对应点F在DA的延长线上，则四边形BEDF　　（填“是”或“不是”）“直等补”四边形；

(2)、如图2，已知四边形ABCD是“直等补”四边形，AB＝BC＝10，CD＝2，AD＞AB，过点B作BE⊥AD于E.
①过C作CF⊥BF于点F，试证明：BE＝DE，并求BE的长；
②若M是AD边上的动点，求△BCM周长的最小值.

查看试题解析
22. 如图，已知二次函数y＝ax²-4x+c的图象经过点A（-1，-1）和点B（3，-9）.

(1)、求该二次函数的表达式；

(2)、直接写出抛物线的对称轴及顶点坐标；

(3)、点P（m，m）与点Q均在该函数图象上（其中m＞0），且这两点关于抛物线的对称轴对称，求m的值及点Q到x轴的距离.

查看试题解析