广西柳州市柳北区鱼峰区2023年九年级第一次联考数学试题

试卷更新日期：2023-04-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $⊙ O$ 的半径为 $6 c m$ ，点P到圆心O的距离 $P O = 8 c m$ ，则点P的位置是（）

A、在 $⊙ O$ 内 B、在 $⊙ O$ 上 C、在 $⊙ O$ 外 D、不能确定

查看试题解析
3. 如图，点A、B、C为 $⊙ O$ 上的点， $∠ A O B = 60 °$ ，则 $∠ A C B =$ （）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $60 °$

查看试题解析
4. 将一元二次方程 $3 x^{2} = 5 x - 1$ 写成一般形式，下列等式正确的是（）

A、 $3 x^{2} - 5 x - 1 = 0$ B、 $3 x^{2} + 5 x - 1 = 0$ C、 $3 x^{2} - 5 x + 1 = 0$ D、 $3 x^{2} + 5 x + 1 = 0$

查看试题解析
5. 在平面直角坐标系 $x O y$ 中，点 $A (2 ， - 3)$ 绕着点O旋转 $180 °$ 后得到点 $B (- 2 ， n)$ 则n的值为（）

A、3 B、 $- 3$ C、2 D、 $- 2$

查看试题解析
6. 下列说法不正确的是（）

A、某种彩票的中奖率是 $\frac{1}{100}$ ，说明每买100张彩票，一定有1张中奖. B、“篮球队员在罚球线上投篮一次，投中”为随机事件. C、“三角形任意两边之和小于第三边”是不可能事件. D、“在同一年出生的367人中，至少有两人的生日相同”是必然事件.

查看试题解析
7. 如图，在 $△ A B C$ 中，点 $D 、 E$ 分别是边 $A B 、 A C$ 的中点，则 $△ A D E$ 与 $△ A B C$ 的面积之比为（）

A、 $2 ： 1$ B、 $4 ： 1$ C、 $1 ： 2$ D、 $1 ： 4$

查看试题解析
8. 把二次函数 $y = 2 x^{2} - 1$ 向右平移2个单位长度，再向下平移4个单位长度后得到的解析式是（）

A、 $y = 2 {(x - 4)}^{2} - 3$ B、 $y = 2 {(x + 4)}^{2} - 3$ C、 $y = 2 {(x + 2)}^{2} - 5$ D、 $y = 2 {(x - 2)}^{2} - 5$

查看试题解析
9. 已知点 $A (3 ， y_{1})$ ， $B (4 ， y_{2})$ ，是抛物线 $y = {(x - 2)}^{2} + 3$ 上的两点，则 $y_{1}$ ， $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
10. 某市轨道交通正式进行运营，从甲地到乙地轨道交通公司共设计了132种往返车票，则这段路线路有多少个站点？假设这段线路有x个站点，根据题意，下面列出的方程正确的是（）

A、 $\frac{1}{2} x (x + 1) = 132$ B、 $\frac{1}{2} x (x - 1) = 132$ C、 $x (x + 1) = 132$ D、 $x (x - 1) = 132$

查看试题解析
11. 如图，点A是反比例图数y＝ $\frac{m}{x}$ （x＜0）图象上一点，AC⊥x轴于点C，与反比例函数y＝ $\frac{n}{x}$ （x＜0）图象交于点B，AB＝2BC，连接OA、OB，若△OAB的面积为3，则m+n＝（）

A、-4 B、-6 C、-8 D、-12

查看试题解析
12. 如图，直线 $y = - x + 4$ 与坐标轴交于A、B两点，点C为坐标平面内一点， $B C = 1$ ，点M为线段 $A C$ 的中点，连接 $O M$ ，则线段 $O M$ 的最小值是（）

A、 $2 \sqrt{2} + \frac{1}{2}$ B、 $2 \sqrt{2} - \frac{1}{2}$ C、1 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

13. 关于x的一元二次方程 $x^{2} + x - a = 0$ 有实数根，则a的取值范围是.

查看试题解析
14. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形，若 $∠ B = 115 °$ ，则 $∠ D$ 的度数为 .

查看试题解析
15. 为估计种子的发芽率，做了10次试验.每次种了1000颗种子，发芽的种子都是950颗左右，预估该种子的发芽率是.

查看试题解析
16. 如图，某学生利用一根长1米的标杆 $E C$ 测量一棵树的高度，测得 $B C = 3$ 米， $C A = 1$ 米，那么树的高度 $D B$ 为米.

查看试题解析
17. 如图，在Rt $△$ ABC中，∠C＝90°，AC＝6，BC＝8，且 $△$ ABC的三边都与⊙O相切，则AO＝.

查看试题解析
18. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 交x轴于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，交y轴的负半轴于C，顶点为D.下列结论：① $b c < 0$ ；② $2 a + b = 0$ ；③ $2 a + c > 0$ ；④当 $m \neq 1$ 时， $a + b < a m^{2} + b m$ ；⑤当 $a = 1$ 时， $△ A B D$ 是等腰直角三角形；其中正确的是（填序号）.

查看试题解析

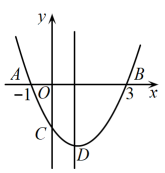
三、解答题

19. 解方程： $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
20. 如图，在边长为1的正方形组成的网格中， $△ A O B$ 的顶点均在格点上，点A、B的坐标分别是 $A (3 ， 2)$ ， $B (1 ， 3)$ . $△ A O B$ 绕点O逆时针旋转 $90 °$ 后得到 $△ A_{1} O B_{1}$ .

(1)、画出旋转后的图形；

(2)、求线段 $O B$ 在旋转过程中所扫过的图形面积.

查看试题解析
21. 如图，在平面直角坐标系xOy中，一次函数 $y_{1} = a x + b (a \neq 0)$ 与反比例函数 $y_{2} = \frac{m}{x}$ （m为常数，且 $m \neq 0$ ）的图象交于点 $A (1 ， 4)$ ， $B (n ， - 2)$

(1)、求该反比例函数与一次函数的解析式；

(2)、根据图象，直接写出满足 $y_{1} \leq y_{2}$ 的x的取值范围.

查看试题解析
22. 如图所示的方格地面上，标有编号A、B、C、D的四个小方格地面是空地，另外5个小方格地面是草坪，除此之外小方格地面完全相同.

(1)、一只自由飞翔的小鸟随意地落在图中所示的9个小方格地面中的一个，则小鸟刚好落在草坪上的概率是；

(2)、现从4个小方格空地中任意选取2个种植草坪，则刚好选取编号为A和C的2个小方格空地种植草坪的概率是多少？请用画树状图或列表的方法说明.

查看试题解析
23. 如图，在预防新冠肺炎疫情期间，某校在校门口用塑料膜围成一个临时隔离区，隔离区一面靠长为 $18 m$ 的墙（隔离区靠墙这面不需要塑料膜），隔离区分成两个区域，中间用塑料膜隔开，已知整个隔离区塑料膜总长为 $30 m$ ，如果隔离区出入口的大小不计，并且隔离区靠墙的面不能超过墙长，设垂直于墙的一边为 $A B$ 为 $x m$ ，隔离区面积为 $S m^{2}$ .

(1)、求S关于x的函数解析式；

(2)、如果要围成面积为 $63 m^{2}$ 的隔离区，那么 $A B$ 的长为多少？

(3)、求隔离区 $A B C D$ 面积的最大值.

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 分别交 $B C 、 A C$ 边于点D、F.过点D作 $D E ⊥ C F$ 于点E

(1)、求证： $D E$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 半径为5，且 $A F - D E = 2$ ，求 $E F$ 的长.

查看试题解析
25. 阅读下列材料：
材料1：对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，如果方程有两个实数根为 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ ；一元二次方程的这种根与系数的关系，最早是由法国数学家韦达（1540-1603）发现的，因此，我们把这个关系称为韦达定理，灵活运用这个定理有时可以使解题更为简单.
材料2：已知一元二次方程 $x^{2} - x - 1 = 0$ 的两个实数根分别为m，n，求 $m^{2} n + m n^{2}$ 的值.

解： $∵$ 一元二次方程 $x^{2} - x - 1 = 0$ 的两个实数根分别为m，n，

$∴ m + n = 1$ ， $m n = - 1$ ，则 $m^{2} n + m n^{2} = m n (m + n) = - 1 \times 1 = - 1$ .

根据上述材料，结合你所学的知识，完成下列问题：

(1)、材料理解：一元二次方程 $- x^{2} + 2 x + 1 = 0$ 的两个根为 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} =$ . $x_{1} x_{2} =$ .

(2)、类比应用：在（1）的条件下，求 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ 的值.

(3)、思维拓展：已知实数s、t满足 $4 s^{2} + 3 s - 4 = 0$ ， $4 t^{2} + 3 t - 4 = 0$ ，且 $s < t$ ，求 $\frac{1}{s} - \frac{1}{t}$ 的值.

查看试题解析
26. 如图1，拋物线 $y = a x^{2} + b x - 1$ 与x轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C.

(1)、求该拋物线的函数表达式；

(2)、在平面直角坐标系内是否存在一点P使得以A、B、C、P为顶点的四边形为平行四边形？若存在，请直接写出所有满足该条件的点P的坐标；若不存在，请说明理由；

(3)、如图2，若点D在该抛物线上且横坐标为2，直线l与抛物线交于A，D两点，点M在y轴上，当 $∠ A D M = 45 °$ 时，求点M的坐标.

查看试题解析