黑龙江省大庆市名校2022-2023学年高一下学期物理4月阶段考试试卷

试卷更新日期：2023-04-10 类型：月考试卷

进入出卷网下载

一、选择题（本题共12小题，每小题4分，共48分。在每小题给出的四个选项中，第1题~第8题只有一个选项是符合题目要求的；第9题~第12题有多个选项是符合题目要求的，全部选对的得4分，选对但不全的得2分，有选错的得0分）

1. 在物理学建立、发展的过程中，下列说法正确的是（）

A、开普勒对第谷观测的行星数据进行了多年研究，得出了万有引力定律 B、卡文迪什进行了“月一地检验”，将天体间的力和地球上物体的重力统一起来 C、引力常量的普适性是万有引力定律正确性的有力证据 D、天王星被人们称为“笔尖下发现的行星”

查看试题解析
2. 2022年7月“力箭一号”（ZK—1A）运载火箭采用“一箭六星”的方式，成功将六颗卫星送入预定轨道。“力箭一号”运载火箭是四级固体运载火箭，起飞重量135吨，起飞推力200吨，总长30米，芯级直径2.65米，首飞状态整流罩直径2.65米，500公里太阳同步轨道运载能力1500公斤。下列说法正确的是（）

A、信息中的“吨、米”是均为国际单位制中的基本单位 B、“力箭一号”点火瞬间，加速度为零 C、“力箭一号”点火瞬间，所携带的卫星处于失重状态 D、“力箭一号”加速上升过程中，所携带的卫星处于超重状态

查看试题解析
3. 地球公转轨道接近圆，但彗星运动轨道则是一个非常扁的椭圆，如图为地球与哈雷彗星绕日运动的示意图。设哈雷彗星运动轨道近日点和远日点与太阳中心的距离分别为 $r_{1}$ 和 $r_{2}$ ，则以下说法正确的是（）

A、哈雷彗星在近日点的加速度小于地球的加速度 B、哈雷彗星在近日点的线速度比在远日点的线速度小 C、地球与太阳的连线和哈雷彗星与太阳的连线在任意相等时间内扫过的面积相等 D、哈雷彗星在近日点和远日点的加速度大小之比 $a_{1} ： a_{2} = r_{2}^{2} ： r_{1}^{2}$

查看试题解析
4. 如图所示，两根相同的轻细线下端分别悬挂两小球A和B，细线上端固定于同一点。若两小球绕共同的竖直轴在水平面内做匀速圆周运动，则两小球在运动的过程中，下列说法正确的是（）

A、小球A的线速度大于小球B的线速度 B、小球A的线速度小于小球B的线速度 C、小球A的向心力大于小球B的向心力 D、小球A的向心力小于小球B的向心力

查看试题解析
5. 如图所示，铁路转弯处外轨应略高于内轨，火车必须按规定的速度行驶，此时火车与铁轨无挤压，则转弯时（）

A、火车所需向心力沿斜面方向指向弯道内侧 B、速度一定时，弯道半径越大，火车所需向心力越小 C、火车的速度若小于规定速度，火车将做离心运动 D、若路基倾角为 $θ$ ，无论火车是否按规定速度行驶，铁轨对火车的支持力总等于 $\frac{m g}{\cos θ}$

查看试题解析
6. 在2022年2月5日北京冬奥会上，我国选手夺得短道速滑混合团体接力奥运冠军！短道速滑比赛中运动员的最后冲刺阶段如图所示，设甲、乙两运动员在水平冰面上恰好同时到达虚线 $P Q$ ，然后分别沿半径为 $r_{1}$ 和 $r_{2} (r_{2} > r_{1})$ 的滑道做匀速圆周运动，运动半个圆周后匀加速冲向终点线。假设甲、乙两运动员质量相等，他们做圆周运动时所受向心力大小相等，直线冲刺时的加速度大小也相等。下列判断中正确的是（）

A、在做圆周运动时，甲先完成半圆周运动 B、在直线加速阶段，甲、乙所用的时间相等 C、在冲刺时，甲、乙到达终点线时的速度相等 D、在直线加速阶段，甲滑行的平均速度大于乙滑行的平均速度

查看试题解析
7. 已知太阳的质量大约是月亮质量的 $2.7 \times 10^{7}$ 倍，太阳到地球的距离大约是月球到地球距离的 $3.9 \times 10^{2}$ 倍，若太阳对地球的引力大小为 $F_{1}$ ，月亮对地球的引力大小为 $F_{2}$ ，则 $\frac{F_{1}}{F_{2}}$ 约为（）

A、130 B、178 C、226 D、274

查看试题解析
8. 如图所示，蜘蛛在地面与竖直墙壁间结网，蛛丝 $A B$ 与水平地面之间的夹角为 $45 °$ ， A到地面的距离为 $1m$ ，已知重力加速度g取 ${10m/s}^{2}$ ，空气阻力不计，若蜘蛛从竖直墙上距地面 $0 .6m$ 的C点以水平速度 $v_{0}$ 跳出，要到达蛛丝，水平速度 $v_{0}$ 至少为（）

A、 $\sqrt{2} m/s$ B、 $2m/s$ C、 $2 \sqrt{2} m/s$ D、 $2 \sqrt{3} m/s$

查看试题解析
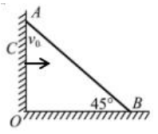9. 宇航员在星球A表面将一小钢球以某一初速度竖直向上抛出，测得小钢球上升的最大高度为h，小钢球从抛出到落回星球表面的时间为t，不计空气阻力，忽略该星球的自转，已知星球A的半径为R（R远大于h），星球A为密度均匀的球体，引力常量为G，下列说法正确的是（）

A、星球A表面的重力加速度为 $\frac{2 h}{t^{2}}$ B、星球A表面的重力加速度为 $\frac{8 h}{t^{2}}$ C、星球A的密度为 $\frac{3 h}{2 π G t^{2} R}$ D、星球A的密度为 $\frac{6 h}{π G t^{2} R}$

查看试题解析
10. 如图所示的水平圆盘上有一原长为 $l_{0}$ 的轻质弹簧，弹簧的一端固定于圆心处，另一端与质量为m的滑块相连，滑块与圆盘之间的动摩擦因数为 $μ$ ，初始时，滑块与圆心之间的距离为l且保持静止。现使圆盘绕过圆心的竖直轴转动， $F_{f}$ 为滑块与圆盘之间的摩擦力的大小，最大静摩擦力等于滑动摩擦力，从零开始逐渐增大圆盘角速度 $ω$ 至某一较大值的过程中，关于 $F_{f}$ 与 $ω^{2}$ 图像可能正确的是（）

A、 B、 C、 D、

查看试题解析
11. 某架飞机在进行航空测量时，需要严格按照从南到北的航线进行飞行。如果在无风时飞机相对地面的速度是 $300km/h$ ，飞行过程中航路上有速度为 $25km/h$ 的持续东风。则（）

A、飞机的飞行方向为北偏西为 $θ$ 角度，且 $\sin θ = \frac{1}{12}$ B、飞机的飞行方向为北偏东为 $θ$ 角度，且 $\sin θ = \frac{1}{12}$ C、飞机实际的飞行速度约为 $83m/s$ D、如果所测地区的南北长度为 $450km$ ，完成测量需要约 $1 .5h$

查看试题解析
12. 如图为离心式转速表中离心器的结构示意图，质量为m的两个重锤利用四根等长的轻质连杆与质量不计的活动套环及固定套环连接，固定套环固定在竖直杆上，竖直杆可绕通过自身的竖直轴自由转动，两个套环间连接着一根轻质弹簧，弹簧的原长为L。离心器不转动时弹簧长度为 $1.5 L$ ，当离心器以角速度 $ω_{0}$ 转动时，弹
簧恰好处于原长。忽略摩擦阻力及其他阻力，重力加速度为g，以下关于离心器说法正确的是（）

A、弹簧的劲度系数 $k = \frac{m g}{L}$ B、弹簧的劲度系数 $k = \frac{2 m g}{L}$ C、角速度 $ω_{0}$ 的大小为 $ω_{0} = \sqrt{\frac{g}{L}}$ D、角速度 $ω_{0}$ 的大小为 $ω_{0} = \sqrt{\frac{2 g}{L}}$

查看试题解析

二、实验题（本题共2个小题，每空2分，满分16分）

13. 某同学设计了如图甲所示的装置来研究小车的加速度与所受合力的关系。将装有力传感器的小车放置于水平长木板上，缓慢向小桶中加入细砂，直到小车刚开始运动为止，记下传感器的最大示数 $F_{0}$ 。再将小车放回原处并按住，继续向小桶中加入细砂，记下传感器的示数 $F_{1}$ 。释放小车，记录小车运动时传感器的示数 $F_{2}$ ，最大静摩擦力等于滑动摩擦力。

(1)、接通频率为 $50Hz$ 的交流电源，释放小车，打出如图乙所示的纸带。从比较清晰的点起，每5个点取一个计数点，量出相邻计数点之间的距离，则小车的加速度 $a =$ ${m/s}^{2}$ ．（保留两位有效数字）

(2)、同一次实验中， $F_{1}$ $F_{2}$ （选填“<”、“=”或“>”）．

(3)、改变小桶中砂的重力，多次重复实验，获得多组数据，描绘小车加速度a与F的关系如图丙。不计纸带与计时器间的摩擦。图像中F是实验中测得的（）

A、 $F_{1}$ B、 $F_{2}$ C、 $F_{1} - F_{0}$ D、 $F_{2} - F_{0}$

查看试题解析
14. 某学校学生进行探究向心力的大小与质量、角速度和半径的关系实验。A组同学利用向心力演示器如图1所示。图2是演示器部分原理示意图：两转臂上黑白格的长度相等；A、B、C为三根固定在转臂上的挡板，可与转臂上做圆周运动的实验球产生挤压，从而提供向心力。图1中的标尺可以显示出两球所受向心力的大小关系。

(1)、A组同学下列操作正确的是__________（填正确答案标号）。

A、探究F的大小与r间的关系时，应将相同的小球分别放在挡板A处和挡板B处，并将皮带套在两边半径相等的变速塔轮上 B、探究F的大小与r间的关系时，应将相同的小球分别放在挡板B处和挡板C处，并将皮带套在两边半径相等的变速塔轮上 C、探究F的大小与 $ω$ 间的关系时，应将相同的小球分别放在挡板A处和挡板C处，并将皮带套在两边半径不同的变速塔轮上 D、探究F的大小与 $ω$ 间的关系时，应将相同的小球分别放在挡板B处和挡板C处，并将皮带套在两边半径不同的变速塔轮上

(2)、A组同学实验时，将皮带与半径比为3：1轮②和轮⑤相连，将质量分别为 $2 m$ 和m的球分别放在挡板B、C位置，转动手柄、则标尺1和标尺2显示的向心力之比为。

(3)、B组同学通过如图3所示装置进行实验。滑块套在水平杆上，随水平杆一起绕竖直杆做匀速圆周运动，力传感器通过一细绳连接滑块，用来测量向心力F的大小。滑块上固定一遮光片，宽度为b，光电门可以记录遮光片通过的时间，测得旋转半径为R。滑块随杆匀速圆周运动，每经过光电门一次，通过力传感器和光电门就同时获得一组向心力F和角速度 $ω$ 的数据。B组同学以F为纵坐标，以（填“ $Δ t$ ”“ $\frac{1}{Δ t}$ ”“ $\frac{1}{Δ t^{2}}$ ”）为横坐标，可在坐标纸中描出数据点作一条如图4所示直线，图线斜率为k，则滑块的质量为（用k、R、b表示）；图线不过坐标原点的原因是。

查看试题解析

三、计算题（本题共3小题，共计36分，应写出必要的文字说明、方程式和重要演算步骤，只写最后答案不得分。有数值计算的题，答案应明确写出数值和单位。）

15. 如图所示，一长为l的轻杆的一端固定在水平转轴上，另一端固定一质量为m的小球，轻杆随转轴在竖直平面内做角速度为 $ω$ 的匀速圆周运动，重力加速度为g，A、B两点与O点在同一水平直线上，C、D分别为圆周的最高点和最低点，求：

(1)、小球运动到水平位置A时，求杆对球的作用力的大小；

(2)、小球在D点与C点相比，杆对小球的作用力大小的差值。

查看试题解析
16. 自由式滑雪女子大跳台比赛场地可简化为如图所示的示意图。在比赛的空中阶段可将运动员视为质点，运动员从倾角为 $α = 30 °$ 的斜面顶端O点以 $v_{0} = 64.8 km/h$ 的初速度飞出，初速度方向与斜面的夹角为 $θ = 60 °$ ，图中虚线为运动员在空中的运动轨迹，A为轨迹的最高点，B为轨迹上离斜面最远的点，C为过B点作竖直线与斜面的交点，不计空气阻力，取重力加速度 $g = 10 {m/s}^{2}$ 。求：

(1)、运动员从O点运动到A点的时间；

(2)、O、C两点间的距离。

查看试题解析
17. 如图所示，一粗细均匀、质量为M的圆管置于倾角 $θ = 30 °$ 的光滑斜面顶端，圆管下端距斜面底端的固定弹性挡板距离为L，上端塞有一质量为m的小球。圆管由静止自由下滑，运动方向始终与挡板垂直，并与挡板发生多次弹性碰撞（碰撞前后，圆管速度大小不变，方向相反），且每次碰撞时间极短。已知 $M = 4 m$ ，小球和圆管之间的滑动摩擦力大小为 $2 m g$ ， g为重力加速度的大小，不计空气阻力。

(1)、求圆管第一次与挡板碰撞后的瞬间，圆管和小球各自的加速度大小；

(2)、圆管第一次与挡板碰撞弹回上滑过程中，球没有从圆管中滑出，求圆管上滑的最大距离；

(3)、圆管第三次与挡板碰撞弹回上滑过程中，球仍没有从圆管中滑出，求圆管长度应满足的条件（结果保留2位小数）。

查看试题解析