2022-2023学年浙教版数学八年级下册5.2菱形 课后测验
试卷更新日期:2023-04-09 类型:同步测试
一、单选题(每题4分,共40分)
-
1. 菱形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四个角都相等2. 在一组对边平行的四边形中,增加一个条件,使得这个四边形是菱形,那么增加的条件可以是( )A、另一组对边相等,对角线相等 B、另一组对边相等,对角线互相垂直 C、另一组对边平行,对角线相等 D、另一组对边平行,对角线相互垂直3. 矩形、菱形都具有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角线垂直、平分且相等4. 张师傅应客户要求加工4个菱形零件.在交付客户之前,需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,下列条件中能使成为菱形的是( )
5. 如图,下列条件中能使成为菱形的是( ) A、 B、 C、 D、6. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若菱形的周长为16,OE的长为( )
A、 B、 C、 D、6. 如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若菱形的周长为16,OE的长为( )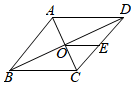 A、2 B、1 C、4 D、37. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
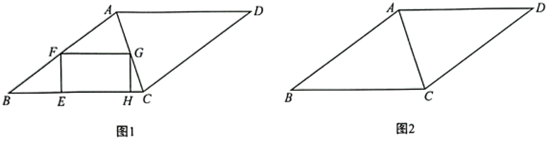
A、2 B、1 C、4 D、37. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( ) A、24 B、48 C、72 D、968. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( )
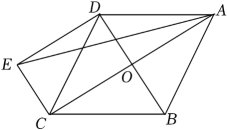
A、24 B、48 C、72 D、968. 如图1,在菱形ABCD中,对角线AC、BD相交于O,要在对角线BD上找两点M、N,使得四边形AMCN是菱形,现有图2中的甲、乙两种方案,则正确的方案是( ) A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是9. 如图,周长为24的菱形中, , 点E,F分别是边上的动点,点P为对角线上一动点,则线段的最小值为( )
A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是9. 如图,周长为24的菱形中, , 点E,F分别是边上的动点,点P为对角线上一动点,则线段的最小值为( ) A、 B、 C、 D、10. 如图,将矩形纸片 分别沿 、 折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形 为菱形,② ,③若 ,则四边形 的面积为 ,④ ,其中正确的说法有( )个.
A、 B、 C、 D、10. 如图,将矩形纸片 分别沿 、 折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形 为菱形,② ,③若 ,则四边形 的面积为 ,④ ,其中正确的说法有( )个. A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(每空5分,共30分)
-
11. 如图,四边形ABCD是菱形,如果AB=5,那么菱形ABCD的周长是 .
 12. 如图,在菱形 中, , ,则菱形 的面积为 .
12. 如图,在菱形 中, , ,则菱形 的面积为 . 13. 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为.
13. 如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为. 14. 如图,菱形ABCD中,对角线AC、BD相交于点O,点E为AC上一点,连接DE,AB=CE=5AE,BD=8,则DE的长为 .
14. 如图,菱形ABCD中,对角线AC、BD相交于点O,点E为AC上一点,连接DE,AB=CE=5AE,BD=8,则DE的长为 . 15. 如图,在菱形ABCD的外侧,作等边△DCE,连接AE、DE.若对角线AC=AB,则∠DEA=度.
15. 如图,在菱形ABCD的外侧,作等边△DCE,连接AE、DE.若对角线AC=AB,则∠DEA=度. 16. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 .
16. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 .
三、作图题(共12分)
-
17. 如图,在边长为1的小正方形组成的的网格中,给出了以格点(网格线的交点)为端点的线段 , .

⑴在图中画出以为边的 , 使为钝角,平行四边形周长为;
⑵在图中画出以为边的菱形 , 使其面积为20;
⑶连接 , 请直接写出线段的长.
四、解答题(共6题,共68分)
-
18. 如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
 19. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.
19. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.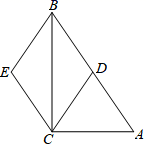 20. 如图,在四边形 中, 是 的垂直平分线, 是 上一点, 交 于 ,连接 . ,试证明四边形 是菱形.
20. 如图,在四边形 中, 是 的垂直平分线, 是 上一点, 交 于 ,连接 . ,试证明四边形 是菱形.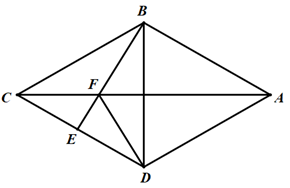 21. 如图,在菱形中,对角线 , 交于点 , 过点作的垂线,垂足为点 , 延长到点 , 使 , 连接 .
21. 如图,在菱形中,对角线 , 交于点 , 过点作的垂线,垂足为点 , 延长到点 , 使 , 连接 .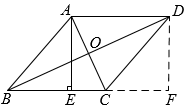 (1)、求证:四边形是矩形;(2)、若 , , 求的长.
(1)、求证:四边形是矩形;(2)、若 , , 求的长.
-