备考2023年中考数学计算能力训练12 求方差

试卷更新日期：2023-04-09 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 在样本方差的计算公式S²＝ $\frac{1}{10}$ [（x₁-20）²+（x₂-20）²+…+（x₁₀-20）²]中，数字10和20分别表示样本的（　　）

A、容量和方差 B、标准差和平均数 C、容量和平均数 D、平均数和容量

查看试题解析
2. 在一次射击练习中，甲、乙两人前后5次射击的成绩如下表（单位：环）：
甲
10
7
10
8
10
乙
7
10
9
10
9
则这次练习中，甲、乙两人成绩的方差大小（）

A、 ${S_{甲}}^{2} > {S_{乙}}^{2}$ B、 ${S_{甲}}^{2} = {S_{乙}}^{2}$ C、 ${S_{甲}}^{2} < {S_{乙}}^{2}$ D、无法确定

查看试题解析
3. 如图是甲、乙两人6次投篮测试（每次投篮10个）成绩的统计图，甲、乙两人测试成绩方差分别记作 ${S_{甲}}^{2}$ ， ${S_{乙}}^{2}$ ，则下列结论正确的是（）

A、 ${S_{甲}}^{2} < {S_{乙}}^{2}$ B、 ${S_{甲}}^{2} > {S_{乙}}^{2}$ C、 ${S_{甲}}^{2} = {S_{乙}}^{2}$ D、无法确定

查看试题解析
4. 淘气统计一组数据142，140，143，136，149，139，得到它们的方差为 $S_{0}^{2}$ ．奇思将这组数据中的每一个数都减去140，得到一组新数据2，0，3，－4，9，－1，计算得出这组新数据的方差为 $S_{1}^{2}$ ．则 $S_{0}^{2}$ 与 $S_{1}^{2}$ 的关系为（）

A、 $S_{0}^{2} > S_{1}^{2}$ B、 $S_{0}^{2} < S_{1}^{2}$ C、 $S_{0}^{2} = S_{1}^{2}$ D、 $S_{0}^{2} + S_{1}^{2} = 1$

查看试题解析
5. 下列方差最大的一组数据是（）

A、6，6，6，6，6 B、5，6，6，6，7 C、4，5，6，7，8 D、3，3，6，9，9

查看试题解析
6. 一个样本为1，3，2，2，a，b，c，已知这个样本的众数为 $3$ ，平均数为2，那么这个样本的方差为（）

A、 $\frac{3}{7}$ B、 $\frac{4}{7}$ C、 $\frac{5}{7}$ D、 $\frac{8}{7}$

查看试题解析
7. 现有甲组数据：1、2、3、4、5，乙组数据：11、12、13、14、15；若甲、乙两组的方差分别为a、b，则a、b的关系是（）

A、 $a = b$ B、 $a = 10 + b$ C、 $a < b$ D、 $a > b$

查看试题解析
8. 已知 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 、 $x_{5}$ 是按从小到大顺序排列的5个连续整数，若将这组数据变为 $x_{1} + 1$ 、 $x_{2} + 1$ 、 $x_{3}$ 、 $x_{4} - 1$ 、 $x_{5} - 1$ ，则这组新数据与原来相比（）

A、平均数变大 B、中位数变小 C、极差变大 D、方差变小

查看试题解析
9. 如果一组数据 $x_{1}$ ， $x_{2}$ ， …， $x_{n}$ 的平均数为 $\bar{x}$ ，方差为 $s^{2}$ ，则数据 $x_{1} - a$ ， $x_{2} - a$ ， …， $x_{n} - a$ 的平均数和方差分别是（）

A、 $\bar{x}$ ， $s^{2}$ B、 $\bar{x} - a$ ， $s^{2} - a$ C、 $\bar{x} - a$ ， $s^{2} - a^{2}$ D、 $\bar{x} - a$ ， $s^{2}$

查看试题解析
10. 第1组数据为：0、0、0、1、1、1，第2组数据为： $\overset{m 个 0}{\overset{︷}{0 ， 0 ， \dots ， 0}}$ 、 $\overset{n 个 1}{\overset{︷}{1 ， 1 ， \dots ， 1}}$ ，其中 $m$ 、 $n$ 是正整数．下列结论：①当 $m = n$ 时，两组数据的平均数相等；②当 $m > n$ 时，第1组数据的平均数小于第2组数据的平均数；③当 $m < n$ 时，第1组数据的中位数小于第2组数据的中位数；④当 $m = n$ 时，第2组数据的方差小于第1组数据的方差．其中正确的是（）

A、①② B、①③ C、①④ D、③④

查看试题解析

二、填空题（每空3分，共30分）

11. 现有两组数据：甲：12，14，16，18；乙：2023，2022，2020，2019，它们的方差分别记作 ${S_{甲}}^{2}$ ， ${S_{乙}}^{2}$ ，则 ${S_{甲}}^{2}$ ${S_{乙}}^{2}$ （用“>”“=”“<”）.

查看试题解析
12. 有甲、乙两组数据，如表所示：甲、乙两组数据的方差分别为 $s_{甲}^{2}$ ， $s_{乙}^{2}$ ，则 $s_{甲}^{2}$ $s_{乙}^{2}$ （填“>”，“<”或“=”）.
甲
10
12
13
14
16
乙
12
12
13
14
14

查看试题解析
13. 已知一组数据分别为：93，93，88，81，94，91，则这组数据的方差为．

查看试题解析
14. 一组数据2022，2022，2022，2022，2022的方差是．

查看试题解析
15. 如果一组数据3，5，x，6，8的众数为3，那么这组数据的方差为 .

查看试题解析
16. 数据 $x_{1} ， x_{2} ， x_{3} ， x_{4}$ 的平均数是4，方差是3，则数据 $x_{1} + 1 ， x_{2} + 1 ， x_{3} + 1 ， x_{4} + 1$ 的平均数和方差分别是，．

查看试题解析
17. 射击运动员小东10次射击的成绩（单位：环）：7.5，8，7.5，8.5，9，7，7，10，8.5，8．这10次成绩的平均数是8.1，方差是0.79，如果小东再射击一次，成绩为10环，则小东这11次成绩的方差0.79．（填“大于”、“等于”或“小于”）

查看试题解析
18. 现有5名同学的身高分别为165，172，168，170，175（单位：厘米）．增加1名身高为170的同学后，这6名同学身高的平均数和方差与原来相比，平均数（填“变大”、“变小”“不变”），方差（填“变大”、“变小”、“不变”）．

查看试题解析

三、解答题（共7题，共60分）

19. 某排球队6名场上队员的身高（单位：cm）是180，184，188，190，192，194.现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员身高的方差会变化吗？通过计算说明你的理由。

查看试题解析
20. 如图，是甲、乙两名射击运动员一次训练中10次射击环数折线统计图.选出方差小的计算方差.

查看试题解析
21. 某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务，这两家厂生产的皮具款式和材料都符合要求，因此只需要检测皮具质量的克数是否稳定.现从两家提供的样品中各抽查10件，测得它们的质量如下（单位：克）
甲：500，499，500，500，503，498，497，502，500，501，
乙：499，500，498，501，500，501，500，499，500，502
你认为该选择哪一家制造厂？

查看试题解析
22. 某市举行学科知识竞赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．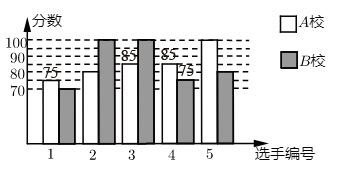

查看试题解析
23. 某校举办国学知识竞赛，设定满分10分，学生得分均为整数.在初赛中，甲、乙两组（每组10人）学生成绩如下（单位：分）
甲组：5，6，6，6，6，6，7，9，9，10.
乙组：5，6，6，6，7，7，7，7，9，10.
组别
平均数
中位数
众数
方差
甲组
7
$a$
6
2.6
乙组
$b$
7
$c$
${S_{乙}}^{2}$

(1)、以上成绩统计分析表中 $a =$ ， $b =$ ， $c =$ ；

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中属中游略偏上!”观察上面表格判断，小明可能是组的学生；

(3)、从平均数和方差看，若从甲、乙两组学生中选择一个成绩较为稳定的小组参加决赛，应选哪个组？并说明理由.

查看试题解析
24. 为提高学生对计算机的兴趣，某校举办计算机汉字输入比赛．甲、乙两组各有10名学生参赛，两组学生每分钟输入汉字的个数如下：
输入汉字（个）
132
133
134
135
136
137
甲组人数（人）
1
0
1
5
2
1
乙组人数（人）
0
1
4
1
2
2

(1)、请将下表中的相关数据补充完整：
组
众数（个）
中位数（个）
平均数（个）
方差
甲组
135
135
乙组
134.5
1.8

(2)、请根据所学的统计知识，从两个不同角度对甲、乙两组学生的比赛成绩进行分析．

查看试题解析

25.

(1)、已知三组数据，通过计算完成填表：

数据	平均数	方差
1，2，3，4，5
11，12，13，14，15
3，6，9，12，15

(2)、【分析数据】请你比较三组数据的大小及统计量的结果，写出其中一些规律性的结论。

(3)、【解决问题】请你用发现的结论来解决以下的问题。

已知数据x₁ ， x₂ ， x₃ ， …，x_n的平均数为a，方差为b，则
（1）数据x₁+3，x₂+3，x₃+3，…，x_n+3的平均数为，方差为。
（2）数据x₁-3，x₂-3，x₃-3，…，x_n-3的平均数为，方差为。
（3）数据3x₁ ， 3x₂ ， 3x₃ ， …，3x_n的平均数为方差为。
（4）数据2x₁-3，2x₂-3，2x₃-3，…，2x_n-3的平均数为，方差为。

查看试题解析

组别	平均数	中位数	众数	方差
甲组	7	$a$	6	2.6
乙组	$b$	7	$c$	${S_{乙}}^{2}$

输入汉字（个）	132	133	134	135	136	137
甲组人数（人）	1	0	1	5	2	1
乙组人数（人）	0	1	4	1	2	2

组	众数（个）	中位数（个）	平均数（个）	方差
甲组	135		135
乙组		134.5		1.8

甲	10	7	10	8	10
乙	7	10	9	10	9

甲	10	12	13	14	16
乙	12	12	13	14	14