备考2023年中考数学计算能力训练7 解一元一次不等式（组）

试卷更新日期：2023-04-09 类型：二轮复习

进入出卷网下载

一、单选题（每题1分，共10分）

1. 若 $a > b$ ，则下列不等式一定成立的是（）

A、 $a - 3 < b - 3$ B、 $\frac{a}{3} > \frac{b}{3}$ C、 $a + 1 < b + 3$ D、 $- a > - b$

查看试题解析
2. 不等式 $3 x > 6$ 的解集在数轴上可表示为（）

A、 B、 C、 D、

查看试题解析
3. 解不等式组 ${\begin{array}{l} 3 - x \geq 4 ① \\ \frac{2}{3} (x + 1) > x - 1 ② \end{array}$ 时，不等式①②的解集在同一数轴上表示正确的是（）

A、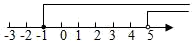 B、 C、 D、

查看试题解析
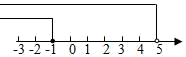4. 一元一次不等式3（7﹣x）≥1＋x的正整数解有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
5. 已知点 $P (m ， n)$ 在直线 $y = - x + 4$ 上，且 $2 m - 5 n \geq 0$ ，则 $()$

A、 $\frac{n}{m}$ 有最大值 $\frac{2}{5}$ B、 $\frac{n}{m}$ 有最小值 C、 $\frac{m}{n}$ 有最大值 $\frac{5}{2}$ D、 $\frac{m}{n}$ 有最小值 $\frac{5}{2}$

查看试题解析
6. 不等式组 ${\begin{array}{l} 4 (x - 1) > 3 x - 2 \\ \frac{2 x + 1}{3} \geq x - 1 \end{array}$ 的整数解是一个一元二次方程的两根，则该方程为（）

A、 $x^{2} + 3 x + 4 = 0$ B、 $x^{2} + 7 x + 12 = 0$ C、 $x^{2} - 3 x + 4 = 0$ D、 $x^{2} - 7 x + 12 = 0$

查看试题解析
7. 关于x的方程3﹣2x＝3（k﹣2）的解为非负整数，且关于x的不等式组 ${\begin{array}{l} x - 2 (x - 1) \leq 3 \\ \frac{2 k + x}{3} \geq x \end{array}$ 有解，则符合条件的整数k的值之和为（）

A、5 B、4 C、3 D、2

查看试题解析
8. 不等式组 ${\begin{array}{l} 5 x - 1 > 3 x - 4 \\ - \frac{1}{3} x \leq \frac{2}{3} - x \end{array}$ 的整数解的和为（）

A、1 B、0 C、-1 D、-2

查看试题解析
9. 定义一种运算： $a * b = {\begin{array}{l} a ， a \geq b \\ b ， a < b \end{array}$ ，则不等式 $(2 x + 1) * (2 - x) > 3$ 的解集是（）

A、 $x > 1$ 或 $x < \frac{1}{3}$ B、 $- 1 < x < \frac{1}{3}$ C、 $x > 1$ 或 $x < - 1$ D、 $x > \frac{1}{3}$ 或 $x < - 1$

查看试题解析
10. 若整数 $a$ 使关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x + 1}{2} \leq \frac{2 x + 5}{6} \\ x - 2 > a \end{array}$ 有解，且使关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} a x + 2 y = 0 \\ x + y = 6 \end{array}$ 的解为正整数，那么所有满足条件的整数 $a$ 的值的积是（）

A、0 B、-80 C、40 D、80

查看试题解析

二、填空题（每空2分，共20分）

11. 不等式 $5 x - 5 < 2 (2 + x)$ 的正整数解是.

查看试题解析
12. 满足不等式 $3 (2 + x) > 2 x$ 的负整数可以是（写出一个即可）.

查看试题解析
13. 已知关于x的不等式组 ${\begin{array}{l} 2 x + 3 \geq x + m \\ \frac{2 x + 5}{3} - 3 < 2 - x \end{array}$ 无解，则 $\frac{1}{m}$ 的取值范围是．

查看试题解析
14. 不等式组 ${\begin{array}{l} 16 x > 24 x - 32 \\ 9 x > 7 x - 6 \end{array}$ 的解集是．

查看试题解析
15. 不等式组 ${\begin{array}{l} 3 (x - 1) + 2 \leq 5 x + 3 \\ \frac{x}{3} < 1 - \frac{x - 1}{5} \end{array}$ 的解集为．

查看试题解析
16. 在一元一次不等式组 ${\begin{array}{l} 2 x + 1 > 0 \\ x - 5 \leq 0 \end{array}$ 的解集中，整数解有个．

查看试题解析
17. 已知关于x的不等式组 ${\begin{array}{l} x - a < 0 ， \\ 2 x - 1 \geq 7 \end{array}$ 至少有两个整数解，且存在以3，a，7为边的三角形，则a的整数解有个．

查看试题解析
18. 当x满足 ${\begin{array}{l} 2 x < 4 x - 4 \\ \frac{1}{3} (x - 6) > \frac{1}{2} (x - 6) \end{array}$ 时，方程 $x^{2} - 2 x - 5 = 0$ 的根是．

查看试题解析
19. 已知正整数 $a$ ， $b$ ， $c$ 均小于5，存在整数 $m$ 满足 $2022 + 1000 m = 2^{a} + 2^{b} + 2^{c}$ ，则 $m (a + b + c)$ 的值为 .

查看试题解析
20. 如图，点A为数轴上一点，对应的实数为a.若﹣a＜b＜a﹣1，请写出一个符合条件的整数b的值.

查看试题解析

三、计算题（共12题，共75分）

21. 解不等式： $\frac{1}{2} (x - 3) < \frac{1}{3} - 2 x$ .

查看试题解析
22. 解不等式组： ${\begin{array}{l} 3 x - 5 > 2 (x - 2) \\ \frac{x}{2} > x - 1 \end{array}$

查看试题解析
23. 解不等式组： ${\begin{array}{l} 2 x + 1 \geq 3 x + 3 \\ x + \frac{1}{3} < \frac{2 + x}{3} \end{array}$ .

查看试题解析
24. 解不等式组： ${\begin{array}{l} 2 (x - 1) \geq - 4 \\ \frac{3 x - 6}{2} < x - 1 \end{array}$ ，并写出它的正整数解.

查看试题解析
25.

(1)、解方程： $\frac{2}{x - 2} = \frac{1 + x}{x - 2} + 1$ ；

(2)、解不等式组： ${\begin{array}{l} x - 1 < 2 x \\ 2 (x - 3) \leq 3 - x \end{array}$ ．

查看试题解析
26.

(1)、解不等式组： ${\begin{array}{l} 2 x - 4 > 3 (x - 2) \\ \frac{x - 7}{2} < 4 x \end{array}$

(2)、计算： $\frac{x + 2}{x^{2} - 1} \div (\frac{1}{x + 1} - 1 - x)$

查看试题解析
27. 不等式组： ${\begin{array}{l} 2 x - 1 < x + 2 \\ \frac{3 x - 4}{4} \leq \frac{2 x - 1}{2} \end{array}$ 并用数轴表示不等式组的解集.

查看试题解析
28. 解不等式组 ${\begin{array}{l} x - 5 < 4 x + 1 \\ 1 - \frac{x - 1}{4} \geq \frac{x}{6} \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
29.

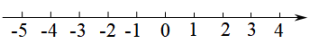(1)、解不等式组 ${\begin{array}{l} x - 3 (x - 2) > 4 ① \\ \frac{2 x - 1}{3} \geq \frac{3 x + 2}{6} - 1 ② \end{array}$ ，并写出该不等式组的最小整数解．

(2)、先化简，再求值：（ $\frac{a^{2} - 9}{a^{2} - 6 a + 9}$ +1）÷ $\frac{a^{2}}{2 a - 6}$ ，其中a＝4sin30°﹣（π﹣3）⁰ ．

查看试题解析
30. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ 2 x + 1 < x - 1 \end{array}$ 并写出该不等式组的最大整数解．

查看试题解析
31. 先化简，再求值： $(\frac{x^{2} - x}{x^{2} - 2 x + 1} + \frac{2}{1 - x}) \div \frac{x - 2}{x^{2} - 1}$ ，其中x是不等式组 ${\begin{array}{l} \frac{1}{2} (x + 1) \leq 2 \\ \frac{x + 2}{3} \geq \frac{x + 3}{4} \end{array}$ 的整数解．

查看试题解析
32. 若数a使关于x的分式方程 $\frac{x + 2}{x - 1} + \frac{a}{1 - x} = 3$ 的解为非负数，且使关于y的不等式组 ${\begin{array}{l} \frac{y - 3}{4} - \frac{y + 1}{3} \geq - \frac{13}{12} \\ 2 (y - a) ＜ 0 \end{array}$ 的解集为 $y \leq 0$ ，求符合条件的所有整数a的积．

查看试题解析

四、综合题（共5题，共45分）

33. 按照如图所示的程序计算：

(1)、若输入a＝﹣9时，求输出结果b的值；

(2)、当输入一个正数a时，输出的结果b不大于﹣11，求输入a的取值范围．

查看试题解析
34. 已知两个整式 $A = x^{2} + 2 x$ ， $B = ■ x + 2$ ，其中系数■被污染．

(1)、若■是-2，化简 $A + B$ ；

(2)、若 $x = 2$ 时， $A + B$ 的值为18．
①说明原题中■是几？
②若再添加一个常数 $a$ ，使 $A + B + a$ 的值不为负数，求 $a$ 的最小值．

查看试题解析
35. 不等式组 ${\begin{array}{l} 2 (1 - x) < x + 8 \\ \frac{3 x - 2}{6} < \frac{x - 1}{3} \end{array}$

(1)、解此不等式组；

(2)、若m是此不等式组的最大整数解，求 $1 + m + m^{2} + \cdot \cdot \cdot + m^{2021} + m^{2022}$ 的值．

查看试题解析
36. 对于实数x，y我们定义一种新运算 $L (x ， y) = a x + b y$ （其中a，b均为非零常数）．等式右边是通常的四则运算，由这种运算得到的数我们称之为线性数，记为 $L (x ， y)$ ，其中x，y叫做线性数的一个数对．若实数x，y都取正整数，我们称这样的线性数为正格线性数，这时的x，y叫做正格线性数的正格数对．

(1)、若 $L (x ， y) = x + 3 y$ ，则 $L (2 ， 1) =$ ， $L (\frac{3}{2} ， \frac{1}{2}) =$ ；

(2)、已知 $L (x ， y) = x + 3 y$ ，若 $L (m ， m - 2)$ 为正格线性数，则满足不等式组 ${\begin{array}{l} 6 \leq L (m ， m - 2) \\ L (m ， m - 2) < 30 \end{array}$ 的所有m的值为．

查看试题解析
37. 若不等式 $($ 组 $)$ 只有 $n$ 个正整数解 $(n$ 为自然数 $)$ ，则称这个不等式 $($ 组 $)$ 为 $n$ 阶不等式 $($ 组 $)$ ．
我们规定：当 $n = 0$ 时，这个不等式 $($ 组 $)$ 为 $0$ 阶不等式 $($ 组 $)$ ．

例如：不等式 $x + 1 < 6$ 只有4个正整数解，因此称其为4阶不等式．

不等式组 ${\begin{array}{l} x + 1 > 2 \\ 2 x - 3 < 7 \end{array}$ 只有3个正整数解，因此称其为3阶不等式组．

请根据定义完成下列问题：

(1)、 $x < \frac{1}{2}$ 是阶不等式； ${\begin{array}{l} x > 1 \\ x - 3 < 0 \end{array}$ 是阶不等式组；

(2)、若关于 $x$ 的不等式组 ${\begin{array}{l} 2 x - 4 a < 0 \\ 2 + 3 x \geq \frac{x + 9}{2} \end{array}$ 是4阶不等式组，求 $a$ 的取值范围；

(3)、关于 $x$ 的不等式组 ${\begin{array}{l} x \geq p \\ x < m \end{array}$ 的正整数解有 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $\dots$ 其中 $a_{1} < a_{2} < a_{3} < a_{4} < \dots$
如果 ${\begin{array}{l} x \geq p \\ x < m \end{array}$ 是 $(m - 3)$ 阶不等式组，且关于 $x$ 的方程 $2 x - m = 0$ 的解是 ${\begin{array}{l} x \geq p \\ x < m \end{array}$ 的正整数解 $a_{3}$ ，请求出 $m$ 的值以及 $p$ 的取值范围．

查看试题解析