2023年中考数学复习考点一遍过——锐角三角函数
试卷更新日期:2023-04-09 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 的值等于( )A、 B、 C、1 D、2. 如图,在中, , , , 则的值为( )
 A、 B、 C、 D、3. 在中, , , 则的值为( )A、 B、 C、 D、24. 已知 , 是锐角,则的度数为( )A、 B、 C、 D、5. 如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( )
A、 B、 C、 D、3. 在中, , , 则的值为( )A、 B、 C、 D、24. 已知 , 是锐角,则的度数为( )A、 B、 C、 D、5. 如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,则的值为( ) A、 B、 C、 D、6. 已知点在平面直角坐标系中,射线与x轴正半轴的夹角为α,那么的值为( )A、 B、2 C、 D、7. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、8. 如图,已知正方形ABCD的边长为2,点E、F分别为AB、BC边的中点,连接AF、DE相交于点M,则∠CDM等于( )
A、 B、 C、 D、6. 已知点在平面直角坐标系中,射线与x轴正半轴的夹角为α,那么的值为( )A、 B、2 C、 D、7. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、8. 如图,已知正方形ABCD的边长为2,点E、F分别为AB、BC边的中点,连接AF、DE相交于点M,则∠CDM等于( ) A、 B、 C、 D、9. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).
A、 B、 C、 D、9. 如图,在中, , 若 , , 点是上一点,且 , 则的值为( ).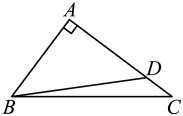 A、 B、 C、 D、10. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( )
A、 B、 C、 D、10. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( ) A、15海里 B、30海里 C、海里 D、海里
A、15海里 B、30海里 C、海里 D、海里二、填空题(每空3分,共15分)
-
11. 在△ABC中,如果 , 则∠C=.12. 一个立方体木箱沿斜面下滑,木箱下滑至如图所示位置时,AB=3m.已知木箱高BE=2m,tan∠BAC=0.5,则木箱端点E距地面AC高度为 m.
 13. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.
13. 如图,在中, , .D是边BC的中点,点E在AB边上,将沿直线DE翻折,使点B落在同一平面内点F处,线段FD交边AB于点G,若时,则.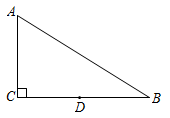 14. 如图,在矩形中, , 点E在上,将矩形沿折叠,点D恰好落在边上的点F处,则的值为 .
14. 如图,在矩形中, , 点E在上,将矩形沿折叠,点D恰好落在边上的点F处,则的值为 . 15. 河堤横断面如图所示,斜坡的坡度(即BC:AC), , 则的长是.
15. 河堤横断面如图所示,斜坡的坡度(即BC:AC), , 则的长是.
三、解答题(共10题,共75分)
-
16. 中, , , , 求边的长度.
 17. 为了增强学生体质,学校鼓励学生多参加体育锻炼,小伟同学马上行动,每天围绕小区进行晨跑锻炼,该小区外围道路近似为如图所示的四边形ABCD,已知四边形ADCE是边长为150米的正方形(点E在边BC上), , 小伟同学每天沿四边形ABCD晨跑1圈,求小伟同学每天晨跑的总路程.
17. 为了增强学生体质,学校鼓励学生多参加体育锻炼,小伟同学马上行动,每天围绕小区进行晨跑锻炼,该小区外围道路近似为如图所示的四边形ABCD,已知四边形ADCE是边长为150米的正方形(点E在边BC上), , 小伟同学每天沿四边形ABCD晨跑1圈,求小伟同学每天晨跑的总路程. 18. 动感单车是一种新型的运动器械.图1是一辆动感单车的实物图,图2是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
18. 动感单车是一种新型的运动器械.图1是一辆动感单车的实物图,图2是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60) 19. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
19. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)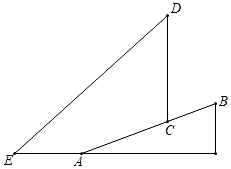 20. 菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:)
20. 菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:) 21. 为进一步加强疫情防控工作,长清区某学校决定安装红外线体温检测仪,对进入测温区域的人员进行快速测温(如图1),其红外线探测点可以在垂直于地面的支杆上下调节(如图2),已知探测最大角()为 , 探测最小角()为 . 若该校要求测温区域的宽度为米,请你帮助学校确定该设备的安装高度 .
21. 为进一步加强疫情防控工作,长清区某学校决定安装红外线体温检测仪,对进入测温区域的人员进行快速测温(如图1),其红外线探测点可以在垂直于地面的支杆上下调节(如图2),已知探测最大角()为 , 探测最小角()为 . 若该校要求测温区域的宽度为米,请你帮助学校确定该设备的安装高度 .(参考数据: , , , , )
 22. 如图,是湘江段江北岸滨江路一段,长度为 , C为南岸一渡口.为了解决两岸交通困难,在渡口C处架桥,垂足为点D.经测量点C在A点的东偏南45°方向,在B点的西偏南60°方向.问:桥长为多少?(结果精确到0.01,参考数据: , .)
22. 如图,是湘江段江北岸滨江路一段,长度为 , C为南岸一渡口.为了解决两岸交通困难,在渡口C处架桥,垂足为点D.经测量点C在A点的东偏南45°方向,在B点的西偏南60°方向.问:桥长为多少?(结果精确到0.01,参考数据: , .) 23. 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废下方点C处有生命迹象,在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:≈1.414,≈1.732,结果精确到0.1)
23. 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废下方点C处有生命迹象,在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:≈1.414,≈1.732,结果精确到0.1)