备考2023年中考数学宁波卷变式阶梯训练:第11-16题
试卷更新日期:2023-04-09 类型:三轮冲刺
一、第十一题
-
1. 请写出一个大于2的无理数:2. 写出一个小于0的无理数 .3. 写出一个比3大且比5小的无理数 .4. 请写出一个整数部分为1的无理数 .5. 写出两个无理数,使它们的和为2 .6. 如图,是一个计算程序.若输入的值为 , 则输出的结果为.
 7. 在实数①﹣ , ② , ③0.3,④ , ⑤ , ⑥ , ⑦0.373737773…(每相邻两个3之间依次多一个7)中,属于无理数的有 .
7. 在实数①﹣ , ② , ③0.3,④ , ⑤ , ⑥ , ⑦0.373737773…(每相邻两个3之间依次多一个7)中,属于无理数的有 .二、第十二题
-
8. 分解因式:x2-2x+1=.9. 分解因式:a4﹣3a2﹣4=.10. 因式分解:b2﹣4b+4= .11. 已知关于 的多项式 ( 为常数)可以用完全平方公式直接述行因式分解,则 的值为.12. 在实数范围内分解因式.13. 分解因式: .14. 因式分解:a²+2ab+b²-3a-3b-4=.
三、第十三题
-
15. 一个不透明的袋子里装有5个红球和6个白球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为16. 一个不透明袋子中装有除颜色外其余都相同的8个球,其中白球5个,黑球3个,从中任意摸出1个球恰好为白球的概率是 .17. 已知每1000个盲盒中常规款有980个, “小隐藏” 15个, “大隐藏” 5个. 现随机抽取1盒, 抽取到的是“大隐藏”的概率为.18. 小颖有两根长度为4cm和9cm的木棒,她想钉一个三角形的木框.现在有5根木棒供她选择,其长度分别为3cm,5cm,10cm,12cm,17cm.小颖随手拿了一根,恰好能够组成一个三角形的概率为 .19. 一个质地均匀的小正方体,6个面分别标有数字1、2、2、3、5、5.若随机投掷一次小正方体,则朝上一面的数字是5的概率为.学习电学知识后,小婷同学用四个开关 , 一个电源和一个灯泡设计了一个电路图,任意闭合其中一个开关,则小灯泡发光的概率等于.
 20. 在平面直角坐标系中,作△OAB,其中三个顶点分别是O(0,0),B(1,1),A(x,y)(-2≤x≤2,-2≤y≤2,x,y均为整数),则所作△OAB为直角三角形的概率是 .21. 现有四张正面分别标有数字-1,0,-2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张记作m不放回,再从余下的卡片中取一张记作n.则点P(m,n)在第二象限的概率为概率是 .
20. 在平面直角坐标系中,作△OAB,其中三个顶点分别是O(0,0),B(1,1),A(x,y)(-2≤x≤2,-2≤y≤2,x,y均为整数),则所作△OAB为直角三角形的概率是 .21. 现有四张正面分别标有数字-1,0,-2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张记作m不放回,再从余下的卡片中取一张记作n.则点P(m,n)在第二象限的概率为概率是 .四、第十四题
-
22. 定义一种新运算:对于任意的非零实数a,b,a b= .若(x+1) x= ,则x的值为23. 对于非零的两个有理数a、b,我们给出一种新的运算⊗,规定:a⊗b= , 若1⊗(x+1)=1,则x的值为 .24. 已知a和b两个有理数,规定一种新运算“*”为:a*b=(其中a+b≠0),若m*= , 则m=.25. 定义一种运算☆,规则为 , 根据这个规则,若 , 则x= .26. 对于实数a,b定义一种新运算“”为 , 这里等式右边是实数运算.例如 , 则方程的解 .27. 对于两个不相等的实数a,b,我们规定符号表示a,b中的较小的值,如 , 按照这个规定,方程(其中)的解为.28. , , 等代数式,如果交换m和n的位置,式子的值不变,我们把这样的式子叫做完美对称式. 若关于x,y的分式 是完美对称式,则: ;若完美对称式 满足: ,且 ,则 (用含x的代数式表示).
五、第十五题
-
29. 如图,在△ABC中,AC=2,BC=4,点O在BC上,以OB为半径的圆与AC相切于点A.D是BC边上的动点,当△ACD为直角三角形时,AD的长为
 30. 如图,已知的半径为1,点是外一点,且 . 若是的切线,为切点,连接 , 则 .
30. 如图,已知的半径为1,点是外一点,且 . 若是的切线,为切点,连接 , 则 . 31. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.
31. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.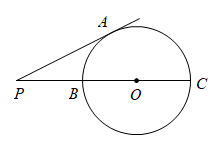 32. 如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=.
32. 如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=.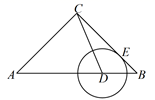 33. 如图,的半径为4,为的直径, , 直线与相切于点 , 交的延长线于点 , 若 , 则的长是.
33. 如图,的半径为4,为的直径, , 直线与相切于点 , 交的延长线于点 , 若 , 则的长是. 34. 如图,⊙O的半径OA=5,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC.当△OAC是直角三角形时,其斜边为 .
34. 如图,⊙O的半径OA=5,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连接OC,AC.当△OAC是直角三角形时,其斜边为 . 35. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=5,BC=12,点P是线段CD上一动点,当半径为4的⊙P与△ABC的一边相切时,CP的长为.
35. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=5,BC=12,点P是线段CD上一动点,当半径为4的⊙P与△ABC的一边相切时,CP的长为.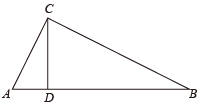
六、第十六题
-
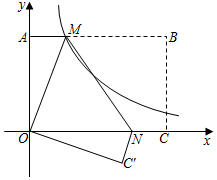
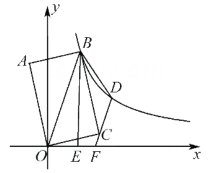
36. 如图,四边形OABC为矩形,点A在第二象限,点A关于OB的对称点为点D,点B,D都在函数y= (x>0)的图象上,BE⊥x轴于点E.若DC的延长线交x轴于点F,当矩形OABC的面积为 时, 的值为 , 点F的坐标为 .
 37. 如图,函数y=(x>0)的图象过矩形OBCD一边的中点,且图象过矩形OAPE的顶点P,若阴影部分面积为6,则k的值为
37. 如图,函数y=(x>0)的图象过矩形OBCD一边的中点,且图象过矩形OAPE的顶点P,若阴影部分面积为6,则k的值为 38. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.
38. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.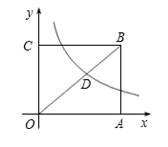 39. 如图,矩形的面积为36,对角线与双曲线相交于点 , 且 , 则的值为.
39. 如图,矩形的面积为36,对角线与双曲线相交于点 , 且 , 则的值为. 40. 如图,反比例函数 的图象经过矩形 对角线的交点 ,分别交 , 于点 、 .若四边形 的面积为12,则 的值为.
40. 如图,反比例函数 的图象经过矩形 对角线的交点 ,分别交 , 于点 、 .若四边形 的面积为12,则 的值为.