备考2023年中考数学宁波卷变式阶梯训练:第6-10题
试卷更新日期:2023-04-09 类型:三轮冲刺
一、第六题
-
1. 已知圆锥的底面半径为4cm,母线长为6cm,则圆锥的侧面积为( )A、36πcm2 B、24πcm2 C、16πcm2 D、12πcm22. 已知圆锥的底面半径为2,母线长为6,则它的侧面展开图的面积是( )A、12 B、24 C、12π D、24π3. 如图是某圆锥的主视图和左视图,该圆锥的侧面积是( )
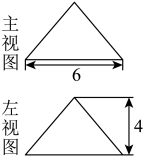 A、15π B、16π C、20π D、25π4. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、5. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( )
A、15π B、16π C、20π D、25π4. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、5. 蒙古包可以近似地看作由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2m,圆锥的高AC=1.5m,圆柱的高CD=2.5m,则下列说法错误的是( ) A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm26. 如图,从一个边长为2m的正六边形ABCDEF铁皮上剪出一个扇形CAE,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为( )
A、圆柱的底面积为4πm2 B、圆柱的侧面积为10πm2 C、圆锥的母线AB长为2.25m D、圆锥的侧面积为5πm26. 如图,从一个边长为2m的正六边形ABCDEF铁皮上剪出一个扇形CAE,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为( )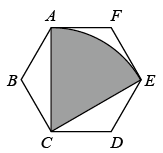 A、 B、 C、 D、7. 如图,从一块半径为2m的圆形铁皮上剪出一个扇形ABC,且经过圆心O.如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为( )m
A、 B、 C、 D、7. 如图,从一块半径为2m的圆形铁皮上剪出一个扇形ABC,且经过圆心O.如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为( )m A、2 B、1 C、 D、
A、2 B、1 C、 D、二、第七题
-
8. 如图,在Rt△ABC中,D为斜边AC的中点,E为BD上一点,F为CE中点.若AE=AD,DF=2,则BD的长为( )
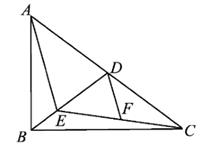 A、 B、3 C、 D、49. 如图,在中, , D,E分别是 , 的中点,F是上一点, , 连接 , , 若 , 则的长度为( )
A、 B、3 C、 D、49. 如图,在中, , D,E分别是 , 的中点,F是上一点, , 连接 , , 若 , 则的长度为( )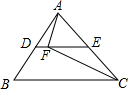 A、8 B、10 C、12 D、1410. 如图,在中, , 是的中点,延长至点 , 使 , 连接 , 为中点,连接若 , , 则的长为( )
A、8 B、10 C、12 D、1410. 如图,在中, , 是的中点,延长至点 , 使 , 连接 , 为中点,连接若 , , 则的长为( )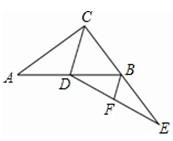 A、5 B、4 C、6 D、811. 如图,在中, , 、分别是、的中点,延长至点 , 使 , 连接、、若 , 则( )
A、5 B、4 C、6 D、811. 如图,在中, , 、分别是、的中点,延长至点 , 使 , 连接、、若 , 则( ) A、3 B、 C、 D、412. 如图,点O是矩形的对角线的中点,点E为的中点.若 , 则的周长为( )
A、3 B、 C、 D、412. 如图,点O是矩形的对角线的中点,点E为的中点.若 , 则的周长为( ) A、10 B、 C、 D、1413. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )
A、10 B、 C、 D、1413. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )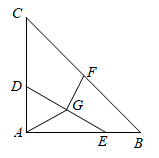 A、 B、 C、 D、414. 如图,在△ABC中, , 点D是AB的中点,将△ACD沿CD对折得△A′CD.连接 , 连接AA′交CD于点E,若 , , 则CE的长为( )
A、 B、 C、 D、414. 如图,在△ABC中, , 点D是AB的中点,将△ACD沿CD对折得△A′CD.连接 , 连接AA′交CD于点E,若 , , 则CE的长为( ) A、4cm B、5cm C、6cm D、7cm
A、4cm B、5cm C、6cm D、7cm三、第八题
-
15. 我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十;粝米三十.今有米在十斗桶中,不知其数.满中添粟而春之,得米七斗,问故米几何?”意思为: 50 斗谷子能出30斗米,即出米率为 .今有米在容量为10斗的桶中,但不知道数量是多少.再向桶中加满谷子,再舂成米,共得米7斗.问原米有米多少斗?如果设原来有米x斗,向桶中加谷子y斗,那么可列方程组为( )A、 B、 C、 D、16. 《九章算术》共收有246个数学问题,分为九章,其中第八章“方程”篇中记载了这样一道题:“今有甲乙二人持钱不知其数,甲得乙半而钱八十,乙得甲太半而钱亦八十.问甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱80.如果乙得到甲所有钱的 , 那么乙也共有钱80.若设甲、乙原本各持钱x,y,则根据题意可列方程组为( )A、 B、 C、 D、17. 我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上.乙说得甲九只,两家之数相当.二人闲坐恼心肠,画地算了半晌.”翻译成现代文,其大意如下:甲乙两人隔一条沟放牧,二人心里暗中合计.甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.请问甲乙各有多少只羊呢?设甲有羊x只,乙有羊y只,则正确的方程组是( )A、 B、 C、 D、18. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有个,甜果有个,则可列方程组为( )A、 B、 C、 D、19. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚黄金重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )A、 B、 C、 D、20. 我国明代数学家程大位所著《算法统宗》中记载了一道有趣的题目:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”题目大意是:100个和尚分100个馒头,刚好分完.大和尚1人分3个馒头,小和尚3人分一个馒头.问大、小和尚各有多少人?若大和尚有x人,小和尚有y人.则下列方程或方程组中① ;② ;③3x+ (100-x)=100;④ y+3(100-y)=100正确的有( )A、0个 B、1个 C、2个 D、3个21. 《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟的方程组形式表述出来,就是 在图2所示的算筹图中有一个图形被墨水覆盖了,如果图2所表示的方程组中x的值为3,则被墨水所覆盖的图形为( )
 A、
A、 B、
B、 C、
C、 D、
D、
四、第九题
-
22. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<223. 已知二次函数y=x2-2x+c的图象经过点P(-1,y1)和Q(m,y2).若y1<y2 , 则m的取值范围是( )A、-1<m<3 B、1<m<3 C、m<-1或m>3 D、m<-124. 已知点 , 在抛物线(m是常数)上,若 , , 则下列大小比较正确的是( )A、 B、 C、 D、25. 若二次函数的图象经过 , , , 四点,则 , , 的大小关系正确的是( )A、 B、 C、 D、26. 设函数 , .直线的图象与函数 , 的图象分别交于点 , , 得( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则27. 点P(x1 , y1),Q(x2 , y2)在抛物线y=ax2-4ax+2(a>0)上,若对于t<x1<t+1,t+2<x2<t+3,都有y1≠y2 , 则t的取值范围是( )A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-128. 小明研究二次函数 (b为常数)性质时,得到如下结论:
①对于任意实数m,m(m-2b)≥1-2b始终成立,则b=1;②这个函数的顶点始终在抛物线 上;③在-1≤x≤5范围内,y的值最大时,x=-1,点(m1 , p)与点(m2 , p)(m1≠m2)在这个函数图象上,则m1+m2>4;④点(b-2n,y1)与点(b+n,y2)(n≠0)在这个函数图象上,则y1<y2其中错误的结论个数是( )
A、1 B、2 C、3 D、4五、第十题
-
29. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
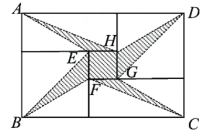 A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积30. 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积30. 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( ) A、(m—n)2 B、(m+n)2 C、2mn D、m2-n231. 两个全等的矩形 和矩形 如图放置, 且 恰好过点 . 过点 作 平行 交 于 . 知道下列哪个式子的值, 即可求出图中阴影部分的面积( )
A、(m—n)2 B、(m+n)2 C、2mn D、m2-n231. 两个全等的矩形 和矩形 如图放置, 且 恰好过点 . 过点 作 平行 交 于 . 知道下列哪个式子的值, 即可求出图中阴影部分的面积( )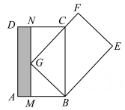 A、 B、 C、 D、32. 如图,从一个大正方形中裁去面积为和的两个小正方形,则剩余部分(阴影部分)的面积等于( )
A、 B、 C、 D、32. 如图,从一个大正方形中裁去面积为和的两个小正方形,则剩余部分(阴影部分)的面积等于( )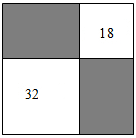 A、 B、 C、 D、33. 如图,正方形AMNP和正方形EFGH是两个全等的正方形,将它们按如图的方式放置在正方形ABCD内,若求阴影图形的面积,则只需知道( )
A、 B、 C、 D、33. 如图,正方形AMNP和正方形EFGH是两个全等的正方形,将它们按如图的方式放置在正方形ABCD内,若求阴影图形的面积,则只需知道( )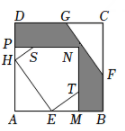 A、△AHE的面积 B、五边形HETNS的面积 C、△EMT的面积 D、正方形AMNP的面积
A、△AHE的面积 B、五边形HETNS的面积 C、△EMT的面积 D、正方形AMNP的面积

