冲刺2023中考——数学模拟考场仿真演练卷十
试卷更新日期:2023-04-08 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 如图,在△ABC中,点D、E分别在边AB、AC上,若DE∥BC, ,DE=6cm,则BC的长为( )
 A、9cm B、12cm C、15cm D、18cm2. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.
A、9cm B、12cm C、15cm D、18cm2. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.袋子 糖果
红色
黄色
绿色
总计
甲袋
2颗
2颗
1颗
5颗
乙袋
4颗
2颗
4颗
10颗
若小明从甲、乙两个袋子中各随机摸出一颗糖果,则他从甲袋比从乙袋( )
A、摸出红色糖果的概率大 B、摸出红色糖果的概率小 C、摸出黄色糖果的概率大 D、摸出黄色糖果的概率小3. 如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是( )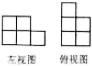 A、7 B、8 C、9 D、104. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、5. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )
A、7 B、8 C、9 D、104. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、5. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有( )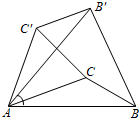 A、①②③ B、①②④ C、①③④ D、②③④6. 如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点点F,∠BOF=65°,则∠AOD为( )
A、①②③ B、①②④ C、①③④ D、②③④6. 如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点点F,∠BOF=65°,则∠AOD为( ) A、70° B、65° C、50° D、45°7. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( )
A、70° B、65° C、50° D、45°7. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( ) A、 B、 C、 D、8. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
A、 B、 C、 D、8. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )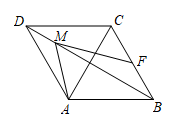 A、1 B、 C、 D、29. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、2010. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( )
A、1 B、 C、 D、29. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、2010. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(每空3分,共18分)
-
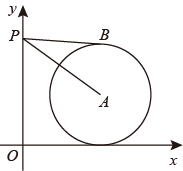
11. 已知 ,则12. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
 13. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .
13. 如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD, , 则k= .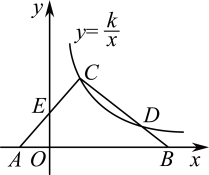 14. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .
14. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .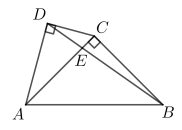 15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.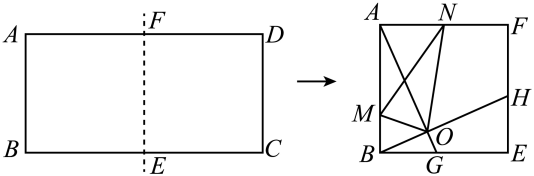 16. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.
16. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.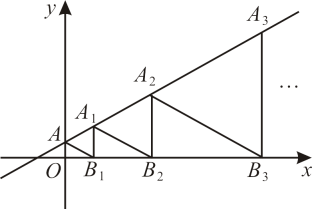
三、解答题(共8题,共72分)
-
17.(1)、先化简再求值: , 其中m=4.(2)、解不等式组并将解集表示在所给的数轴上.
 18. 为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
18. 为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题: (1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.19. 如图,在中,以AB为直径作交AC、BC于点D、E,且D是AC的中点,过点D作于点G,交BA的延长线于点H.
(1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.19. 如图,在中,以AB为直径作交AC、BC于点D、E,且D是AC的中点,过点D作于点G,交BA的延长线于点H.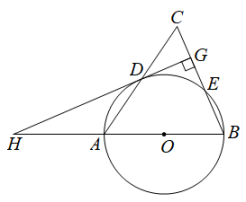 (1)、求证:直线HG是的切线;(2)、若 , 求CG的长.20. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC;
(1)、求证:直线HG是的切线;(2)、若 , 求CG的长.20. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC; (1)、求直线AB与双曲线的解析式.(2)、求△ABC的面积21. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .
(1)、求直线AB与双曲线的解析式.(2)、求△ABC的面积21. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .参考数据:
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
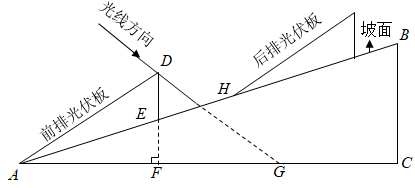 (1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?22. 已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.
(1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?22. 已知△ABC中,∠ACB=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动,同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,设运动的时间为t秒.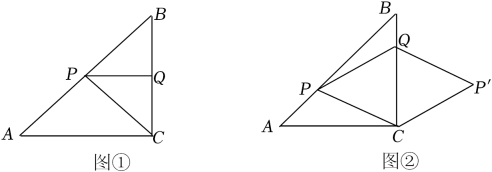 (1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?23. 回顾:用数学的思维思考
(1)、如图①,若PQ⊥BC,求t的值;(2)、如图②,将△PQC沿BC翻折至△P′QC,当t为何值时,四边形QPCP′为菱形?23. 回顾:用数学的思维思考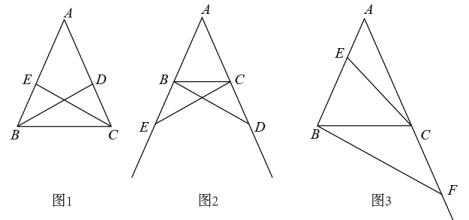 (1)、如图1,在△ABC中,AB=AC.
(1)、如图1,在△ABC中,AB=AC.①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)、猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
(3)、探究:用数学的语言表达如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
24. 如图,已知抛物线经过和两点,直线与x轴相交于点C,P是直线上方的抛物线上的一个动点,轴交于点D.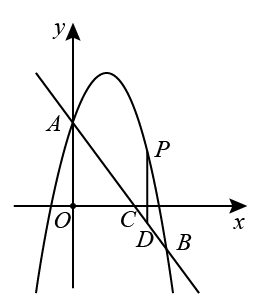 (1)、求该抛物线的表达式;(2)、若轴交于点E,求的最大值;(3)、若以A,P,D为顶点的三角形与相似,请直接写出所有满足条件的点P,点D的坐标.
(1)、求该抛物线的表达式;(2)、若轴交于点E,求的最大值;(3)、若以A,P,D为顶点的三角形与相似,请直接写出所有满足条件的点P,点D的坐标.