浙教版数学九年级上学期期末重难点复习:二次函数难题汇总卷
试卷更新日期:2023-04-07 类型:复习试卷
一、第一节内容
-
1. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )
 A、
A、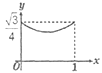 B、
B、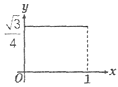 C、
C、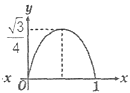 D、
D、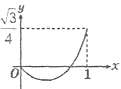 2. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
2. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )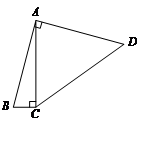
A、 B、 C、 D、3. 如图所示,已知抛物线在坐标系中的顶点为 ,且与坐标轴交点为 点.(相关数据见图中标示)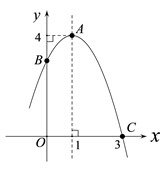 (1)、求该抛物线的解析式;(2)、求△ 的面积;(3)、在 轴上求作一点 使△ 得周长最小,求出满足条件的点 的坐标.4. 如图,在平面直角坐标系中,抛物线 ,与 轴交于点 与 轴交于点 、 .且点 , ,点 为抛物线上的一动点.
(1)、求该抛物线的解析式;(2)、求△ 的面积;(3)、在 轴上求作一点 使△ 得周长最小,求出满足条件的点 的坐标.4. 如图,在平面直角坐标系中,抛物线 ,与 轴交于点 与 轴交于点 、 .且点 , ,点 为抛物线上的一动点. (1)、求二次函数的解析式;(2)、如图1,过点 作 平行于 轴,交抛物线于点 ,若点 在 的上方,作 平行于 轴交 于点 ,连接 , ,当 时,求点 坐标;(3)、设抛物线的对称轴与 交于点 ,点 在直线 上,当以点 、 、 、 为顶点的四边形为平行四边形时,请直接写出点 的坐标.5. 已知抛物线 与x轴交于点 ,点 ,与y轴交于点C,顶点为点D.
(1)、求二次函数的解析式;(2)、如图1,过点 作 平行于 轴,交抛物线于点 ,若点 在 的上方,作 平行于 轴交 于点 ,连接 , ,当 时,求点 坐标;(3)、设抛物线的对称轴与 交于点 ,点 在直线 上,当以点 、 、 、 为顶点的四边形为平行四边形时,请直接写出点 的坐标.5. 已知抛物线 与x轴交于点 ,点 ,与y轴交于点C,顶点为点D.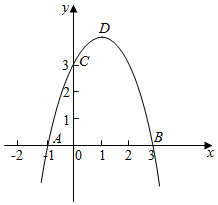 (1)、求抛物线的解析式;(2)、若点P在抛物线上,点Q在x轴上,当以点A、C、P、Q为顶点的四边形是平行四边形时,请直接写出点P的坐标;(3)、已知点 , ,在抛物线对称轴上,找一点F,使 的值最小.此时,在抛物线上是否存在一点K,使 的值最小?若存在,求出点K的坐标;若不存在,请说明理由.6. 如图,抛物线y=ax2 + bx + c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3).
(1)、求抛物线的解析式;(2)、若点P在抛物线上,点Q在x轴上,当以点A、C、P、Q为顶点的四边形是平行四边形时,请直接写出点P的坐标;(3)、已知点 , ,在抛物线对称轴上,找一点F,使 的值最小.此时,在抛物线上是否存在一点K,使 的值最小?若存在,求出点K的坐标;若不存在,请说明理由.6. 如图,抛物线y=ax2 + bx + c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3).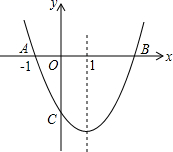 (1)、求抛物线y= ax2 + bx + c 的解析式;(2)、求△AOC和△BOC的面积比;(3)、在对称轴上是否存在一个P点,使△PAC的周长最小.若存在,请你求出点P的坐标;若不存在,请你说明理由.7. 如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y= x2+bx﹣2的图象过C点.
(1)、求抛物线y= ax2 + bx + c 的解析式;(2)、求△AOC和△BOC的面积比;(3)、在对称轴上是否存在一个P点,使△PAC的周长最小.若存在,请你求出点P的坐标;若不存在,请你说明理由.7. 如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y= x2+bx﹣2的图象过C点.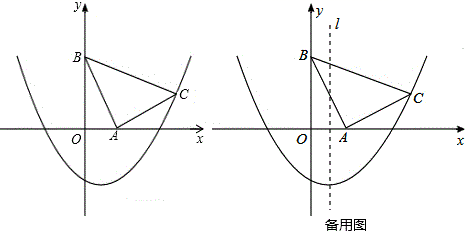 (1)、求抛物线的解析式;(2)、平移该抛物线的对称轴所在直线l,当l移动到何处时,恰好将△ABC的面积分为相等的两部分?8. 如图①,抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)、求抛物线的解析式;(2)、平移该抛物线的对称轴所在直线l,当l移动到何处时,恰好将△ABC的面积分为相等的两部分?8. 如图①,抛物线 与 轴交于 , 两点,与 轴交于点 .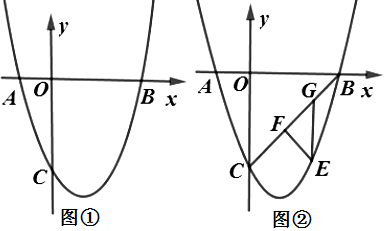
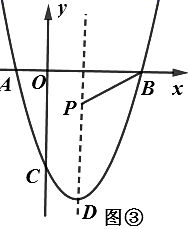 (1)、求抛物线 的解析式;(2)、如图②,连接 ,点 是第三象限内抛物线上的动点,过点 作 于点 , 轴交 于点 ,求 面积的最大值及此时点 的坐标;(3)、如图③,若抛物线的顶点坐标为点 ,点 是抛物线对称轴上的动点,在坐标平面内是否存在点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.9. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在 点上正方 的 处发出一球,羽毛球飞行的高度 与水平距离 之间满足函数表达式 .已知点 与球网的水平距离为 ,球网的高度为 .
(1)、求抛物线 的解析式;(2)、如图②,连接 ,点 是第三象限内抛物线上的动点,过点 作 于点 , 轴交 于点 ,求 面积的最大值及此时点 的坐标;(3)、如图③,若抛物线的顶点坐标为点 ,点 是抛物线对称轴上的动点,在坐标平面内是否存在点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.9. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在 点上正方 的 处发出一球,羽毛球飞行的高度 与水平距离 之间满足函数表达式 .已知点 与球网的水平距离为 ,球网的高度为 . (1)、当 时,①求 的值;
(1)、当 时,①求 的值;②通过计算判断此球能否过网;
(2)、若甲发球过网后,羽毛球飞行到 处时,乙扣球成功。已知点 离点 的水平距离为 ,离地面的高度为 的,求 的值.二、第二节内容
-
10. 已知抛物线y=-x2+bx+c(b,c为常数)经过点(0,-3)、(-6,-3).(1)、求此抛物线的解析式.(2)、此抛物线的顶点坐标为(3)、当-4≤x≤0时,求y的最大值和最小值.(4)、当m≤x≤0时,若y的最大值与最小值之和为2,直接写出m的值.11. 在平面直角坐标系中,二次函数( , m为常数)的图象记作G,图象G上点A的横坐标为2m.(1)、当 , 求图象G的最低点坐标;(2)、平面内有点 . 当AC不与坐标轴平行时,以AC为对角线构造矩形ABCD,AB与x轴平行,BC与y轴平行.
①若矩形ABCD为正方形时,求点A坐标;
②图象G与矩形ABCD的边有两个公共点时,求m的取值范围.
12. 已知抛物线 经过点(0,2),且与 轴交于A、B两点.设k是抛物线 与 轴交点的横坐标;M是抛物线 的点,常数m>0,S为△ABM的面积.已知使S=m成立的点M恰好有三个,设T为这三个点的纵坐标的和.(1)、求c的值;(2)、且接写出T的值;(3)、求 的值.13. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )① ;②;③;④将图象向上平移1个单位后与直线有3个交点.
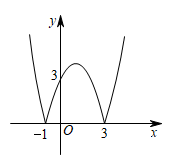 A、①② B、①③ C、②③④ D、①③④14. 在平面直角坐标系中,已知抛物线(m为常数).
A、①② B、①③ C、②③④ D、①③④14. 在平面直角坐标系中,已知抛物线(m为常数). (1)、求此抛物线的顶点坐标.(用含m的式子表示)(2)、当时,抛物线对应的函数值y随x的增大而先增大后减小,求m的取值范围.(3)、将抛物线(m为常数)在y轴右侧的部分沿着直线翻折,翻折后的图像与原抛物线剩余部分合称为图像G.
(1)、求此抛物线的顶点坐标.(用含m的式子表示)(2)、当时,抛物线对应的函数值y随x的增大而先增大后减小,求m的取值范围.(3)、将抛物线(m为常数)在y轴右侧的部分沿着直线翻折,翻折后的图像与原抛物线剩余部分合称为图像G.①当时,在如图的平面直角坐标系中画出图像G.
②当 , 且图像G与直线有且只有两个公共点时,求这两个公共点之间的距离.
③正方形的顶点的坐标为 , 顶点B的坐标为 , 当图像G和正方形的边有且只有四个公共点时,直接写出m的取值范围.
15. 若平面直角坐标系内的点 满足横、纵坐标都为整数,则把点 叫做“整点”.例如: 、 都是“整点”.抛物线 与 轴交于A、 两点,若该抛物线在A、 之间的部分与线段 所围成的区域(包括边界)恰有七个整点,则 的取值范围是( )A、 B、 C、 D、16. 已知抛物线与y轴的交点为A,顶点为P,对称轴为直线m.(1)、求抛物线l的顶点坐标P和对称轴.(2)、抛物线l关于点A对称的抛物线为 , 抛物线的顶点为Q,对称轴为直线n,在直线m和直线n上是否分别存在点E、F,使得四边形为正方形?若存在,请求出a的值;若不存在,请说明理由.17. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
 A、4个 B、3个 C、2个 D、1个18. 如图,已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1 , 0),且1<x1 <2,与y轴交于正半轴.下列结论错误的是( )
A、4个 B、3个 C、2个 D、1个18. 如图,已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1 , 0),且1<x1 <2,与y轴交于正半轴.下列结论错误的是( ) A、4a-2b+c=0 B、当x< 时,y随x增大而增大 C、当x> 时,y随x增大而减小 D、a<b<019. 定义:如果两个函数y1 , y2存在x取同一个值,使得y1=y2 , 那么称y1 , y2互为“等值函数”,对应的x值为y1 , y2的“等值根”.(1)、函数y1= x+b与 是否互为“等值函数”?如果是,求出当b=1时,两函数的“等值根”;如果不是,请说明理由.(2)、如图所示的是y=﹣|x2+2x|的图象,它是由二次函数y=﹣x2﹣2x的图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变得到的.若y1= x+b与y2=﹣|x2+2x|互为“等值函数”,且有两个“等值根”,求b的取值范围.
A、4a-2b+c=0 B、当x< 时,y随x增大而增大 C、当x> 时,y随x增大而减小 D、a<b<019. 定义:如果两个函数y1 , y2存在x取同一个值,使得y1=y2 , 那么称y1 , y2互为“等值函数”,对应的x值为y1 , y2的“等值根”.(1)、函数y1= x+b与 是否互为“等值函数”?如果是,求出当b=1时,两函数的“等值根”;如果不是,请说明理由.(2)、如图所示的是y=﹣|x2+2x|的图象,它是由二次函数y=﹣x2﹣2x的图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变得到的.若y1= x+b与y2=﹣|x2+2x|互为“等值函数”,且有两个“等值根”,求b的取值范围. 20. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( )
20. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( ) A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为为任意实数)21. 如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )
A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为为任意实数)21. 如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( ) A、①③④ B、①②④ C、②③④ D、①②③④
A、①③④ B、①②④ C、②③④ D、①②③④三、第三四节
-
22. 关于的二次函数 , 在时有最大值6,则 .23. 已知抛物线的图象与x轴相交于点A和点 , 与y轴交于点C,连接AC,有一动点D在线段AC上运动,过点D作x轴的垂线,交抛物线于点E,交x轴于点F, , 设点D的横坐标为m.
 (1)、连接AE,CE则的最大面积为;(2)、当时,在平面内存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形,请写出点Q的坐标.24. 二次函数的部分图象如图所示,其对称轴为直线 , 且与轴的一个交点坐标为 , 下列结论:
(1)、连接AE,CE则的最大面积为;(2)、当时,在平面内存在点Q,使以B,C,E,Q为顶点的四边形为平行四边形,请写出点Q的坐标.24. 二次函数的部分图象如图所示,其对称轴为直线 , 且与轴的一个交点坐标为 , 下列结论:①;②;③图象与轴的另一个交点坐标为;④关于的一元二次方程有两个相等的实数根;⑤ . 其中正确的结论个数是( )
 A、2 B、3 C、4 D、525. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
A、2 B、3 C、4 D、525. 如图,抛物线交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.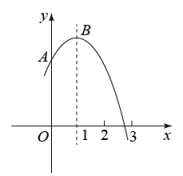
①一元二次方程有两个相等的实数根;②若点 , , 在该函数图象上,则;③将该抛物线先向左平移1个单位,再沿x轴翻折,得到的抛物线表达式是;④在y轴上找一点D,使的面积为1,则D点的坐标为.以上四个结论中正确的个数是( )
A、1个 B、2个 C、3个 D、4个26. 若任意两个正数的和为定值,则它们的乘积会如何变化呢?会不会存在最大值?特例研究:若两个正数的和是1,那么这两个正数可以是:和 , 和 , 和 , …
由于这样的正数有很多,我们不妨设其中一个正数是 , 另外一个正数为 , 那么 , 则 , 所以 , , 可以看出两数的乘积是的二次函数,乘积的最大值转化为求关于的二次函数的最值问题.
方法迁移:
(1)、若两个正数x和y的和是6,其中一个正数为 , 这两个正数的乘积为z,写出z与x的函数关系式,并画出函数图象. (2)、在(1)的条件下,z的最大值为: , 并写出此时函数图象的至少一个性质 .(3)、问题解决:
(2)、在(1)的条件下,z的最大值为: , 并写出此时函数图象的至少一个性质 .(3)、问题解决:由以上题目可知若任意两个正数的和是一个固定的数,那么这两个正数的乘积存在最大值,即对于正数x,y,若x+y是定值,则xy存在最大值.
类比应用:
利用上面所得到的结论,完成填空:
①已知函数与函数 , 则当x=时,取得最大值为;
②已知函数y1=2x-2+m(x≥1),m为正定值,函数y2=-2x+8(x<4),则当x为何值时,取得最大值,最大值是多少?
27. 已知关于的二次函数 , 其中为实数,当-2≤x≤1时,的最小值为4,满足条件的的值为。28. 已知抛物线有最高点.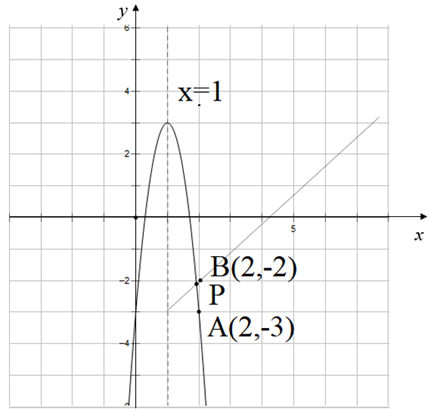 (1)、m0(填“>、=、<”);(2)、求二次函数的最大值(用含m的式子表示);(3)、将抛物线G向右平移m个单位得到抛物线 . 经过探究发现,随着m的变化,抛物线顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;(4)、记(3)所求的函数为H,抛物线G与函数H的图象交于点P,结合图象,求点P的纵坐标的取值范围.
(1)、m0(填“>、=、<”);(2)、求二次函数的最大值(用含m的式子表示);(3)、将抛物线G向右平移m个单位得到抛物线 . 经过探究发现,随着m的变化,抛物线顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;(4)、记(3)所求的函数为H,抛物线G与函数H的图象交于点P,结合图象,求点P的纵坐标的取值范围.
