海南省临高县2023届高三数学模拟考试试卷

试卷更新日期：2023-04-07 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in Z | - 5 \leq x \leq 1}$ ，集合 $B = {- 2 ， - 1 ， 0 ， 1 ， 2}$ ，则集合 $A ∩ B =$ （）

A、 ${- 5 ， - 4 ， 0 ， 1}$ B、 ${- 2 ， - 1 ， 0 ， 1 ， 2}$ C、 ${- 2 ， - 1 ， 0 ， 1}$ D、 ${- 2 ， - 1 ， 0}$

查看试题解析
2. 宁启铁路线新开行“绿巨人”动力集中复兴号动车组，最高时速为 $160 k m / h$ ．假设“绿巨人”开出站一段时间内，速度 $v (m / s)$ 与行驶时间 $t (s)$ 的关系为 $v = 0.4 t + 0.6 t^{2}$ ，则出站后“绿巨人”速度首次达到 $24 m / s$ 时加速度为（）

A、 $6.8 m / s^{2}$ B、 $7.6 m / s^{2}$ C、 $7 m / s^{2}$ D、 $7.8 m / s^{2}$

查看试题解析
3. 复平面内正方形三个顶点分别对应复数 $z_{1} = 1 + 2 i$ ， $z_{2} = - 2 + i$ ， $z_{3} = - 1 - 2 i$ ，则另一个顶点对应的复数为（）

A、 $2 - i$ B、 $5 i$ C、 $- 4 - 3 i$ D、 $2 - i$ ， $5 i$ 或 $- 4 - 3 i$

查看试题解析
4. 下列函数中，最小正周期为 $π$ 的是（）

A、 $y = s i n x$ B、 $y = c o s 2 x$ C、 $y = c o s x$ D、 $y = s i n \frac{1}{2} x$

查看试题解析
5. 若曲线 $y = f (x) = x^{2} + a x + b$ 在点(1，f(1))的切线为 $3 x - y - 2 = 0$ ，则有（）

A、 $a = - 1$ ， $b = 1$ B、 $a = 1$ ， $b = - 1$ C、 $a = - 2$ ， $b = 1$ D、 $a = 2$ ， $b = - 1$

查看试题解析
6. 函数 $f (x) = \log_{a} (2 x - 3) - 4 (a > o 且 a \neq 1)$ 的图象恒过定点（）

A、 $(1, 0)$ B、 $(1, - 4)$ C、 $(2, 0)$ D、 $(2, - 4)$

查看试题解析
7. 给定下列四个命题：
命题①： $a > b ， c > d \Rightarrow a - c > b - d$ ；命题②： $a > b \Rightarrow {(\frac{1}{2})}^{a} < {(\frac{1}{2})}^{b}$ ；
命题③： ${\begin{array}{l} 0 < a < 1 \\ 2 < b < 3 \end{array} \Leftrightarrow {\begin{array}{l} 2 < a + b < 4 \\ 0 < a b < 3 \end{array}$ ；命题④： $a < b < 0 \Rightarrow \frac{b}{a} < \frac{a}{b}$ .
其中真命题的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知 $Δ A B C$ 的三个内角 $A, B, C$ 所对边长分别是 $a, b, c$ ，若 $\frac{sin B - sin A}{sin C} = \frac{\sqrt{3} a + c}{a + b}$ ，则角 $B$ 的大小为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析

二、多选题

9. 一个人的领导力由五种能力—影响力､控制力､决断力､前瞻力和感召力构成.如图是某企业对两位领导人领导力的测评图，每项能力分为三个等级，“一般”记为3分､“较强”记为4分､“很强”记为5分，把分值称为能力指标，则下列判断正确的是（）

A、甲､乙的五项能力指标的均值相同 B、甲､乙的五项能力指标的方差相同 C、如果从控制力､决断力､前瞻力考虑，乙的领导力高于甲的领导力 D、如果从影响力､控制力､感召力考虑，甲的领导力高于乙的领导力

查看试题解析
10. 在平面直角坐标系中，下列方程表示的曲线是椭圆的有（）

A、 $\sqrt{x^{2} + (y - 2)^{2}} + \sqrt{x^{2} + (y + 2)^{2}} = 4$ B、 $\sqrt{(x + 1)^{2} + y^{2}} + \sqrt{(x - 1)^{2} + y^{2}} = 4$ C、 $2 \sqrt{(x - 1)^{2} + y^{2}} = | 4 - x |$ D、 $\sqrt{(x + 2)^{2} + y^{2}} = 2 | 2 + x |$

查看试题解析
11. 下列说法正确的是（）

A、若 $x ， y \in R$ 且 $x + y > 4$ ，则 $x$ ， $y$ 至少有一个大于2 B、 $\forall x \in R$ ， $\sqrt{x^{2}} = x$ C、若 $1 < a < 3$ ， $2 < b < 4$ ，则 $- 2 < 2 a - b < 4$ D、 $\sqrt{x^{2} + 3} + \frac{1}{\sqrt{x^{2} + 3}}$ 的最小值为2

查看试题解析
12. 已知函数 $f (x) = | 2 s i n (2 x - \frac{π}{3}) |$ ，则下列说法中正确的有（）

A、函数 $f (x)$ 的图象关于点 $(\frac{π}{6} ， 0)$ 对称 B、函数 $f (x)$ 图象的一条对称轴是 $x = \frac{π}{6}$ C、若 $x \in [\frac{π}{3} ， \frac{π}{2}]$ ，则函数 $f (x)$ 的最小值为 $\sqrt{3}$ D、若 $f (x_{1}) f (x_{2}) = 4$ ， $x_{1} \neq x_{2}$ ，则 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{2}$

查看试题解析

三、填空题

13. 下列命题中正确的有．
①若 $\vec{a} ， \vec{b} ， \vec{c}$ 是空间三个非零向量，且满足 $\vec{a} \cdot \vec{b} = \vec{c} \cdot \vec{b}$ ，则 $\vec{a} = \vec{c}$ ；
②回归直线一定过样本中心 $(\bar{x} ， \bar{y})$ ．
③若将一组样本数据中的每个数据都加上同一个常数后，则样本的方差不变；
④用相关指数 $R^{2}$ 来刻画回归效果， $R^{2}$ 越接近0，说明模型的拟合效果越好；

查看试题解析
14. 若 ${(1 + x)}^{10} = \sum_{i = 0}^{10} a_{i} {(1 - x)}^{i}$ ，则 $a_{9} =$ .

查看试题解析
15. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a>b>0）的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，其焦距为2 $c$ ，点Q（ $c$ ， $\frac{a}{2}$ ）在椭圆内部，点P是椭圆上动点，且|PF₁|+|PQ|<6|F₁F₂|恒成立.则椭圆离心率的取值范围是.

查看试题解析
16. 在数列 ${a_{n}}$ 中， $a_{1} = 1$ ， $a_{n + 1} = a_{n} + \frac{1}{a_{n}}$ （n∈ $N^{*}$ ），若 $t \in Z$ ，则当 $| a_{7} - t |$ 取得最小值时，整数 $t$ 的值为.

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别是 $a ， b ， c$ ，已知 $t a n C = \frac{s i n B}{1 - c o s B}$ ．

(1)、求证： $△ A B C$ 为等腰三角形；

(2)、若 $△ A B C$ 是钝角三角形，且面积为 $\frac{a^{2}}{4}$ ，求 $\frac{b^{2}}{a c}$ 的值．

查看试题解析
18. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且满足 $a_{3} = 6$ ， $S_{11} = 132$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求数列 ${\frac{1}{S_{n}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
19. 如图，在梯形 $A B C D$ 中， $A B ⊥ A D ， A D / / B C ， A D = 2 A B = 2 B C = 2 ， A E ⊥$ 平面 $A B C D$ ， $C F ⊥$ 平面 $A B C D$ ．

(1)、求证： $C D ⊥ E F$ ；

(2)、 $A E = 2 ， C F = 3$ ，求点 $F$ 到平面 $C D E$ 的距离．

查看试题解析
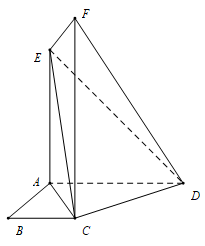20. 已知两定点 $P (- 1 ， 0)$ ， $Q (1 ， 0)$ ，动点 $M$ 满足 $| P M | = 4$ ，线段 $M Q$ 的垂直平分线与线段 $P M$ 相交于点 $N$ ，设点 $N$ 的轨迹为曲线 $C$ ．

(1)、求曲线 $C$ 的方程；

(2)、若直线l：y=kx+m与椭圆 $C$ 相交于A，B两点，且 $k_{O A} \cdot k_{O B} = - \frac{b^{2}}{a^{2}}$ ，判断△AOB的面积是否为定值？若为定值，求出定值；若不为定值，说明理由．

查看试题解析
21. 一个口袋中装有 $n$ 个红球 $(n \geq 5$ 且 $n \in N)$ 和 $5$ 个白球，一次摸奖从中摸两个球，两个球颜色不同则为中奖.

(1)、用 $n$ 表示一次摸奖中奖的概率 $p_{n}$ ；

(2)、若 $n = 5$ ，设三次摸奖（每次摸奖后球放回）恰好有 $X$ 次中奖，求 $X$ 的数学期望 $E X$ ；

(3)、设三次摸奖（每次摸奖后球放回）恰好有一次中奖的概率 $P$ ，当 $n$ 取何值时， $P$ 最大？

查看试题解析
22. 已知函数 $f (x) = (x - 1) e^{x} - a x$ ．

(1)、当 $x > - 1$ 时， $x_{0}$ 是 $y = f (x)$ 的一个极值点且 $f (x_{0}) = - 1$ ，求 $x_{0}$ 及 $a$ 的值；

(2)、已知 $g (x) = x^{2} l n x$ ，设 $h (x) = e^{x} [f^{'} (x) + a]$ ，若 $x_{1} > 1$ ， $x_{2} > 0$ ，且 $g (x_{1}) = h (x_{2})$ ，求 $x_{1} - 2 x_{2}$ 的最小值．

查看试题解析