广东省湛江市2023届高三数学一模试卷

试卷更新日期：2023-04-07 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $i$ 为虚数单位，若 $\frac{1 + i}{1 - b i} = i$ ，则实数 $b =$ （）

A、1 B、-1 C、2 D、-2

查看试题解析
2. 已知R为实数集，集合 $A = {x | \frac{2}{x - 1} < 1}$ ， $B = {x | \frac{1}{2} < 2^{x} < 4}$ ，则图中阴影部分表示的集合为（）

A、 ${x | - 1 < x \leq 3}$ B、 ${x | 2 < x \leq 3}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | - 1 < x < 2}$

查看试题解析
3. 小明在设置银行卡的数字密码时，计划将自己出生日期的后6个数字 $0 ， 5 ， 0 ， 9 ， 1 ， 9$ 进行某种排列得到密码．如果排列时要求两个9相邻，两个0也相邻，则小明可以设置多少个不同的密码（）

A、16 B、24 C、166 D、180

查看试题解析
4. 在平行四边形 $A B C D$ 中， $E$ 为边 $B C$ 的中点，记 $\vec{A C} = \vec{a}$ ， $\vec{D B} = \vec{b}$ ，则 $\vec{A E} =$ （）

A、 $\frac{1}{2} \vec{a} - \frac{1}{4} \vec{b}$ B、 $\frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}$ C、 $\vec{a} + \frac{1}{2} \vec{b}$ D、 $\frac{3}{4} \vec{a} + \frac{1}{4} \vec{b}$

查看试题解析
5. 元宵节是春节之后的第一个重要节日，元宵节又称灯节，很多地区家家户户都挂花灯．下图是小明为自家设计的一个花灯，该花灯由上面的正六棱台与下面的正六棱柱组成，若正六棱台的上、下两个底面的边长分别为40cm和20cm，正六棱台与正六棱柱的高分别为10cm和60cm，则该花灯的体积为（）

A、 $46000 \sqrt{3} c m^{3}$ B、 $48000 \sqrt{3} c m^{3}$ C、 $50000 \sqrt{3} c m^{3}$ D、 $52000 \sqrt{3} c m^{3}$

查看试题解析
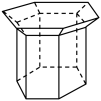6. 已知F为抛物线 $C ： x^{2} = 8 y$ 的焦点，过F的直线 $l$ 与抛物线C交于A，B两点，与圆 $x^{2} + {(y - 2)}^{2} = 4$ 交于D，E两点，A，D在y轴的同侧，则 $| A D | \cdot | B E | =$ （）

A、1 B、4 C、8 D、16

查看试题解析
7. 已知 $a = {(\frac{9}{11})}^{0.1} ， b = l o g_{9} 10 ， c = l g 11$ ，则（）

A、 $b > c > a$ B、 $c > b > a$ C、 $b > a > c$ D、 $c > a > b$

查看试题解析
8. 已知函数 $f (x)$ 及其导函数 $f^{'} (x)$ 的定义域均为R，且 $f (x - 1)$ 为奇函数， $f^{'} (2 - x) + f^{'} (x) = 2$ ， $f^{'} (- 1) = 2$ ，则 $\sum_{i = 1}^{25} f^{'} (2 i - 1) =$ （）

A、13 B、16 C、25 D、51

查看试题解析

二、多选题

9. 某服装生产商为了解青少年的身高和体重的关系，在15岁的男生中随机抽测了10人的身高和体重，数据如下表所示：
编号
1
2
3
4
5
6
7
8
9
10
身高/cm
165
168
170
172
173
174
175
177
179
182
体重/kg
55
89
61
65
67
70
75
75
78
80
由表中数据制作成如下所示的散点图：
由最小二乘法计算得到经验回归直线 $l_{1}$ 的方程为 $\hat{y} = {\hat{b}}_{1} x + {\hat{a}}_{1}$ ，相关系数为 $r_{1}$ ，决定系数为 $R_{1}^{2}$ ；经过残差分析确定 $(168 ， 89)$ 为离群点（对应残差过大），把它去掉后，再用剩下的9组数据计算得到经验回归直线 $l_{2}$ 的方程为 $\hat{y} = {\hat{b}}_{2} x + {\hat{a}}_{2}$ ，相关系数为 $r_{2}$ ，决定系数为 $R_{2}^{2}$ ．则以下结论中正确的有（）

A、 ${\hat{a}}_{1} > {\hat{a}}_{2}$ B、 ${\hat{b}}_{1} > {\hat{b}}_{2}$ C、 $r_{1} < r_{2}$ D、 $R_{1}^{2} > R_{2}^{2}$

查看试题解析
10. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点E，F分别为棱BC与 $D_{1} C_{1}$ 的中点，则下列选项正确的有（）

A、 $A_{1} B / /$ 平面 $A E C_{1}$ B、 $E F$ 与 $B C_{1}$ 所成的角为30° C、 $E F ⊥$ 平面 $B_{1} A C$ D、平面 $A E C_{1}$ 截正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的截面面积为 $2 \sqrt{6}$

查看试题解析
11. 已知 $ω > 0$ ，函数 $f (x) = c o s (ω x + \frac{π}{3})$ ，下列选项正确的有（）

A、若 $f (x)$ 的最小正周期 $T = 2$ ，则 $ω = π$ B、当 $ω = 2$ 时，函数 $f (x)$ 的图象向右平移 $\frac{π}{3}$ 个单位长度后得到 $g (x) = c o s 2 x$ 的图象 C、若 $f (x)$ 在区间 $(\frac{2 π}{3} ， π)$ 上单调递增，则 $ω$ 的取值范围是 $[1 ， \frac{5}{3}]$ D、若 $f (x)$ 在区间 $(0 ， π)$ 上只有一个零点，则 $ω$ 的取值范围是 $(\frac{1}{6} ， \frac{7}{6}]$

查看试题解析
12. 已知 $F_{1} ， F_{2}$ 分别为双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点，点 $A (x_{1} ， y_{1})$ 为双曲线C在第一象限的右支上一点，以A为切点作双曲线C的切线交x轴于点 $B (x_{2} ， 0)$ ，则下列结论正确的有（）

A、 $0 < x_{2} < a$ B、 $∠ F_{1} A B = ∠ F_{2} A B$ C、 $x_{1} x_{2} = a b$ D、若 $c o s ∠ F_{1} A F_{2} = \frac{1}{3}$ ，且 $\vec{F_{1} B} = 3 \vec{B F_{2}}$ ，则双曲线C的离心率 $e = 2$

查看试题解析

三、填空题

13. 已知 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，若 $a_{3} = 10 ， S_{15} = 0$ ，则 $S_{16} =$ ．

查看试题解析
14. $\frac{c o s 70 ° - c o s 20 °}{c o s 65 °} =$ ．

查看试题解析
15. 若函数 $f (x) = e^{x} - a x^{2} - a$ 存在两个极值点 $x_{1} ， x_{2}$ ，且 $x_{2} = 2 x_{1}$ ，则 $a =$ ．

查看试题解析
16. 已知函数 $f (x) = 2 x + 1$ ，记 $f^{(2)} (x) = f (f (x)) = 2 (2 x + 1) + 1 = 4 x + 3$ 为函数 $f (x)$ 的2次迭代函数， $f^{(3)} (x) = f (f (f (x))) = 4 (2 x + 1) + 3 = 8 x + 7$ 为函数 $f (x)$ 的3次迭代函数，…，依次类推， $f^{(n)} (x) = \underset{n 个}{\underset{︸}{f (f (f (\cdot \cdot \cdot f (x) \cdot \cdot \cdot)))}}$ 为函数 $f (x)$ 的n次迭代函数，则 $f^{(n)} (x) =$ ； $f^{(100)} (32)$ 除以17的余数是．

查看试题解析

四、解答题

17. 在△ABC中，内角A，B，C的对边分别为a，b，c，已知 $\frac{b}{a} = 2 c o s (\frac{π}{3} - C)$ ．

(1)、求A；

(2)、若△ABC的面积为 $\frac{3 \sqrt{3}}{2}$ ， $b = 2$ ，求a．

查看试题解析
18. 已知 $S_{n}$ ，为数列 ${a_{n}}$ 的前n项和， $S_{n} = 2 a_{n} - 4 n + 2$ ．

(1)、证明：数列 ${a_{n} + 4}$ 为等比数列；

(2)、设数列 ${\frac{2^{n}}{a_{n} \cdot a_{n + 1}}}$ 的前n项和为 $T_{n}$ ，证明： $T_{n} < \frac{1}{6}$ ．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中， $△ P A B$ 是边长为2的等边三角形，底面 $A B C D$ 为平行四边形，且 $A D = \sqrt{2}$ ， $P B ⊥ B C$ ， $∠ A D C = 45 °$ ．

(1)、证明：点 $P$ 在平面 $A B C D$ 的正投影在直线 $A D$ 上；

(2)、求平面 $P B C$ 与平面 $P D C$ 夹角的余弦值．

查看试题解析
20. 某工厂一台设备生产一种特定零件，工厂为了解该设备的生产情况，随机抽检了该设备在一个生产周期中的100件产品的关键指标（单位： $c m$ ），经统计得到下面的频率分布直方图：
参考公式：直方图的方差 $s^{2} = \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} p_{i}$ ，其中 $x_{i}$ 为各区间的中点， $p_{i}$ 为各组的频率．
参考数据：若随机变量X服从正态分布 $N (μ ， σ^{2})$ ，则 $P (μ - 3 σ \leq X \leq μ + 3 σ) \approx 0.9973$ ， (1)由频率分布直方图估计抽检样本关键指标的平均数 $\bar{x}$ 和方差 $s^{2}$ ．（用每组的中点代表该组的均值）

(1)、已知这台设备正常状态下生产零件的关键指标服从正态分布 $N (μ ， σ^{2})$ ，用直方图的平均数估计值 $\bar{x}$ 作为 $μ$ 的估计值 $\hat{μ}$ ，用直方图的标准差估计值s作为 $σ$ 估计值 $\hat{σ}$ ．
（i）为了监控该设备的生产过程，每个生产周期中都要随机抽测10个零件的关键指标，如果关键指标出现了 $(μ - 3 σ ， μ + 3 σ)$ 之外的零件，就认为生产过程可能出现了异常，需停止生产并检查设备．下面是某个生产周期中抽测的10个零件的关键指标：
0.8
1.2
0.95
1.01
1.23
1.12
1.33
0.97
1.21
0.83
利用 $\hat{μ}$ 和 $\hat{σ}$ 判断该生产周期是否需停止生产并检查设备．
（ii）若设备状态正常，记X表示一个生产周期内抽取的10个零件关键指标在 $(μ - 3 σ ， μ + 3 σ)$ 之外的零件个数，求 $P (X \geq 1)$ 及X的数学期望．
$\sqrt{0.011} \approx 0.105$ ， $\sqrt{0.012} \approx 0.110$ ， $0.997 3^{9} \approx 0.9760$ ， $0.997 3^{10} \approx 0.9733$ ．

查看试题解析
21. 已知 $F_{1} ， F_{2}$ 分别为椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点，椭圆E的离心率为 $\frac{1}{2}$ ，过 $F_{2}$ 且不与坐标轴垂直的直线 $l$ 与椭圆E交于A，B两点， $△ F_{1} A B$ 的周长为8．

(1)、求椭圆E的标准方程；

(2)、过 $F_{1}$ 且与 $l$ 垂直的直线 $l^{'}$ 与椭圆E交于C，D两点，求四边形ACBD面积的最小值．

查看试题解析
22. 已知函数 $f (x) = e^{x} + c o s x - 2$ ．

(1)、证明：函数 $f (x)$ 只有一个零点；

(2)、在区间 $(0 ， + ∞)$ 上函数 $f (x) > a x - s i n x$ 恒成立，求a的取值范围．

查看试题解析

编号	1	2	3	4	5	6	7	8	9	10
身高/cm	165	168	170	172	173	174	175	177	179	182
体重/kg	55	89	61	65	67	70	75	75	78	80