广东省江门市2023届高三数学一模试卷

试卷更新日期：2023-04-07 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 0 ， 1}$ ， $B = {m | m^{2} - 1 \in A ， m - 1 \notin A}$ ，则集合B中所有元素之和为（）

A、0 B、1 C、－1 D、 $\sqrt{2}$

查看试题解析
2. 已知i为虚数单位，复数z满足 $z (1 + i) = | 1 + i |$ ，则 $z =$ （）

A、 $\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i$ B、 $\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} i$ C、 $- \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i$ D、 $- \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} i$

查看试题解析
3. 命题“ $\forall x \in Q$ ， $x^{2} - 5 \neq 0$ ”的否定为（）

A、 $\exists x \notin Q$ ， $x^{2} - 5 = 0$ B、 $\forall x \in Q$ ， $x^{2} - 5 = 0$ C、 $\forall x \notin Q$ ， $x^{2} - 5 = 0$ D、 $\exists x \in Q$ ， $x^{2} - 5 = 0$

查看试题解析
4. 已知多项式 ${(x - 1)}^{10} = a_{0} + a_{1} (x + 1) + a_{2} {(x + 1)}^{2} + ⋯ + a_{10} {(x + 1)}^{10}$ ，则 $a_{7} =$ （）

A、－960 B、960 C、－480 D、480

查看试题解析
5. 设非零向量 $\vec{m}$ ， $\vec{n}$ 满足 $| \vec{m} | = 2$ ， $| \vec{n} | = 3$ ， $| \vec{m} + \vec{n} | = 3 \sqrt{2}$ ，则 $\vec{m}$ 在 $\vec{n}$ 方向上的投影向量为（）

A、 $- \frac{5}{18} \vec{n}$ B、 $\frac{5}{18} \vec{n}$ C、 $- \frac{5}{8} \vec{m}$ D、 $\frac{5}{8} \vec{m}$

查看试题解析
6. 衣柜里有灰色，白色，黑色，蓝色四双不同颜色的袜子，从中随机选4只，已知取出两只是同一双，则取出另外两只不是同一双的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{4}{5}$ C、 $\frac{8}{15}$ D、 $\frac{8}{9}$

查看试题解析
7. 已知等差数列 ${a_{n}}$ （ $n \in N_{+}$ ）的前n项和为 $S_{n}$ ，公差 $d < 0$ ， $\frac{a_{10}}{a_{9}} < - 1$ ，则使得 $S_{n} > 0$ 的最大整数n为（）

A、9 B、10 C、17 D、18

查看试题解析
8. 我们知道按照一定顺序排列的数字可以构成数列，那么按照一定顺序排列的函数可以构成函数列.设无穷函数列 ${f_{n} (x)}$ （ $n \in N_{+}$ ）的通项公式为 $f_{n} (x) = \frac{n^{2} + 2 n x + x^{2} + 1}{(n + x) (n + 1)}$ ， $x \in (0 ， 1)$ ，记 $E_{n}$ 为 $f_{n} (x)$ 的值域， $E = U_{n = 1}^{+ \infty} E_{n}$ 为所有 $E_{n}$ 的并集，则E为（）

A、 $(\frac{5}{6} ， \frac{10}{9})$ B、 $(1 ， \frac{10}{9})$ C、 $(\frac{5}{6} ， \frac{5}{4})$ D、 $(1 ， \frac{5}{4})$

查看试题解析

二、多选题

9. 已知函数 $f (x) = | s i n (2 x - \frac{π}{3}) |$ ，则下列说法正确的是（）

A、 $f (x)$ 的值域为 $[0 ， 1]$ B、 $f (x)$ 的图像关于点 $(\frac{π}{6} ， 0)$ 中心对称 C、 $f (x)$ 的最小正周期为 $π$ D、 $f (x)$ 的增区间为 $[\frac{k π}{2} + \frac{π}{6} ， \frac{k π}{2} + \frac{5 π}{12}]$ （ $k ∈ Z$ ）

查看试题解析
10. 已知曲线 $C ： x^{2} s i n α + y^{2} c o s α = 1 (0 \leq α < π)$ ，则下列说法正确的是（）

A、若曲线 $C$ 表示两条平行线，则 $α = 0$ B、若曲线 $C$ 表示双曲线，则 $\frac{π}{2} < α < π$ C、若 $0 < α < \frac{π}{2}$ ，则曲线 $C$ 表示椭圆 D、若 $0 < α < \frac{π}{4}$ ，则曲线 $C$ 表示焦点在 $x$ 轴的椭圆

查看试题解析
11. 已知函数 $f (x) = x^{2} (x + 2) (x - 1)$ ，则下列说法正确的是（）

A、 $f (x)$ 的图象是轴对称图形 B、 $f (x)$ 的极大值为0 C、 $f (x)$ 的所有极值点之和为 $- \frac{3}{4}$ D、 $f (x)$ 的极小值之积为 $\frac{9}{8}$

查看试题解析
12. 勒洛Franz Reuleaux（1829～1905），德国机械工程专家，机构运动学的创始人.他所著的《理论运动学》对机械元件的运动过程进行了系统的分析，成为机械工程方面的名著.勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触，因此它能像球一样来回滚动.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体.如图所示，设正四面体 $A B C D$ 的棱长为2，则下列说法正确的是（）

A、勒洛四面体能够容纳的最大球的半径为 $2 - \frac{\sqrt{6}}{2}$ B、勒洛四面体被平面 $A B C$ 截得的截面面积是 $2 (π - \sqrt{3})$ C、勒洛四面体表面上交线 $A C$ 的长度为 $\frac{2 π}{3}$ D、勒洛四面体表面上任意两点间的距离可能大于2

查看试题解析

三、填空题

13. 已知 $θ \in (- \frac{π}{2} ， 0)$ ， $c o s 2 θ = \frac{7}{9}$ ，则 $s i n θ$ 的值为.

查看试题解析
14. 椭圆是特别重要的一类圆锥曲线，是平面解析几何的核心，它集中地体现了解析几何的基本思想.而黄金椭圆是一条优美曲线，生活中许多椭圆形的物品，都是黄金椭圆，它完美绝伦，深受人们的喜爱.黄金椭圆具有以下性质：①以长轴与短轴的四个顶点构成的菱形内切圆经过两个焦点，②长轴长，短轴长，焦距依次组成等比数列.根据以上信息，黄金椭圆的离心率为.

查看试题解析
15. 已知直线l过点 $A (1 ， 2 ， 0)$ ，且直线l的一个方向向量为 $\vec{m} = (0 ， - 1 ， 1)$ ，则坐标原点O到直线l的距离d为.

查看试题解析
16. 已知 $f (x) = | l n x |$ ， $x_{1} ， x_{2}$ 是方程 $f (x) = a$ （ $a \in R$ ）的两根，且 $x_{1} < x_{2}$ ，则 $\frac{a}{x_{1} x_{2}^{2}}$ 的最大值是．

查看试题解析

四、解答题

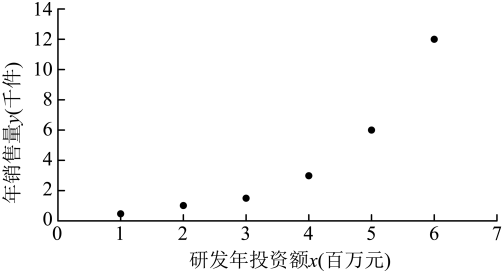
17. 已知数列 ${a_{n}}$ （ $n \in N_{+}$ ）满足 $a_{1} = 1$ ， $a_{n + 1} = \frac{3 n + 3}{n} a_{n}$ ，且 $b_{n} = \frac{a_{n}}{n}$ .

(1)、求数列 ${b_{n}}$ 是通项公式；

(2)、求数列 ${a_{n}}$ 的前n项和 $S_{n}$ .

查看试题解析
18. 在锐角 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $\frac{1}{t a n B}$ ， $\frac{1}{s i n A}$ ， $\frac{1}{t a n C}$ 依次组成等差数列.

(1)、求 $\frac{a^{2}}{b c}$ 的值；

(2)、若 $b > c$ ，求 $\frac{b^{2} + c^{2}}{a^{2}}$ 的取值范围.

查看试题解析
19. 某高科技公司对其产品研发年投资额x（单位：百万元）与其年销售量y（单位：千件）的数据进行统计，整理后得到如下统计表和散点图.
x
1
2
3
4
5
6
y
0.5
1
1.5
3
6
12
$z = l n y$
-0.7
0
0.4
1.1
1.8
2.5
参考公式及数据： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ，
$R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} y_{i}^{2} - n {\bar{y}}^{2}}$ ，
$\sum_{i = 1}^{6} x_{i} z_{i} = - 1 \times 0.7 + 2 \times 0 + 3 \times 0.4 + 4 \times 1.1 + 5 \times 1.8 + 6 \times 2.5 = 28.9$ ， $e^{3.4} = 30$ .

(1)、该公司科研团队通过分析散点图的特征后，计划分别用① $y = b x + a$ 和② $y = e^{d x + c}$ 两种方案作为年销售量y关于年投资额x的回归分析模型，请根据统计表的数据，确定方案①和②的经验回归方程；（注：系数b，a，d，c按四舍五入保留一位小数）

(2)、根据下表中数据，用相关指数 $R^{2}$ （不必计算，只比较大小）比较两种模型的拟合效果哪个更好，并选择拟合精度更高、更可靠的模型，预测当研发年投资额为8百万元时，产品的年销售量是多少？
经验回归方程
残差平方和
$y = b x + a$
$y = e^{d x + c}$
${\sum_{i = 1}^{5} (y_{i} - {\hat{y}}_{i})}^{2}$
18.29
0.65

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是菱形， $O$ 是 $A D$ 的中点，点 $E$ 在 $P C$ 上，且 $A P / /$ 平面 $B O E$ .

(1)、求 $\frac{P E}{E C}$ 的值；

(2)、若 $O P ⊥$ 平面 $A B C D$ ， $O E ⊥ P C$ ， $A B = 2$ ， $∠ B A D = 6 0^{∘}$ ，求直线 $O E$ 与平面 $P B C$ 所成角的正弦值.

查看试题解析
21. 已知M是平面直角坐标系内的一个动点，直线 $M A$ 与直线 $y = x$ 垂直，A为垂足且位于第一象限，直线 $M B$ 与直线 $y = - x$ 垂直，B为垂足且位于第四象限，四边形 $O A M B$ （O为原点）的面积为8，动点M的轨迹为C.

(1)、求轨迹C的方程；

(2)、已知 $T (5 ， 3)$ 是轨迹C上一点，直线l交轨迹C于P，Q两点，直线 $T P$ ， $T Q$ 的斜率之和为1， $t a n ∠ P T Q = 1$ ，求 $△ T P Q$ 的面积.

查看试题解析
22. 已知函数 $f (x) = x - \frac{1}{x} - a l n x$ ，其中 $a \in R$ .

(1)、若 $f (x)$ 的图象在 $x = 1$ 处的切线过点 $(2 ， 1)$ ，求a的值；

(2)、证明： $\forall a > 1$ ， $f (e^{- a}) < 0$ ，其中e的值约为2.718，它是自然对数的底数；

(3)、当 $a > 2$ 时，求证： $f (x)$ 有3个零点，且3个零点之积为定值.

查看试题解析

x	1	2	3	4	5	6
y	0.5	1	1.5	3	6	12
$z = l n y$	-0.7	0	0.4	1.1	1.8	2.5