鲁教版(五四制)2022-2023学年度第二学期七年级数学 证明的必要性 期中复习
试卷更新日期:2023-04-06 类型:复习试卷
一、单选题
-
1. 嘉淇在证明“平行于同一条直线的两条直线平行”时,给出了如下推理过程:
已知:如图,b∥a,c∥a,求证:b∥c;
证明:作直线DF交直线a、b、c分
别于点D、E、F,
∵a∥b,∴∠1=∠4,又∵a∥c,
∴∠1=∠5,
∴b∥c.

小明为保证嘉淇的推理更严谨,想在方框中“∴∠1=∠5”和“∴b∥c”之间作补充,下列说法正确的是( )
A、嘉淇的推理严谨,不需要补充 B、应补充∠2=∠5 C、应补充∠3+∠5=180° D、应补充∠4=∠52. 阅读下列材料,其中①~④步数学依据错误的是( )如图:已知直线 , a⊥b,求证: .
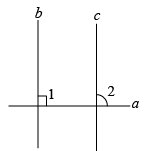
证明:∵(已知),
∴(①垂直的定义).
∵ (已知),
∴(②两直线平行,同位角相等),
∴(③同角的余角相等),
∴(④垂直的定义).
A、① B、② C、③ D、④3. 小英、小亮、小明和小华四名同学参加了“大梦杯”竞赛选拔赛,小亮和小华两个同学的得分和等于小明和小英的得分和;小英与小亮的得分和大于小明和小华的得分和;小华的得分超过小明与小亮的得分和.则这四位同学的得分由小到大的顺序是( )A、小明、小亮、小华、小英 B、小明、小亮、小英、小华 C、小英、小华、小亮、小明 D、小亮、小英、小华、小明4. 有四位同学一起研究一道数学题.如图,已知EF⊥AB , CD⊥AB . 则下列说法正确的是( )甲说:“如果还知道∠CDG=∠BFE , 则能得到∠AGD=∠ACB . ”
乙说:“把甲的已知和结论倒过来,即由∠AGD=∠ACB , 可得到∠CDG=∠BFE . ”
丙说:“∠AGD一定大于∠BFE . ”
丁说:“如果连接GF , 则GF一定平行于AB . ”
 A、甲对乙错 B、乙错丁对 C、甲、乙对 D、乙、丙对5. 如图,四边形ABCD中,AC , BD交于点O , 如果∠BAC=∠DCA , 那么以下四个结论中错误的是( )
A、甲对乙错 B、乙错丁对 C、甲、乙对 D、乙、丙对5. 如图,四边形ABCD中,AC , BD交于点O , 如果∠BAC=∠DCA , 那么以下四个结论中错误的是( ) A、AD∥BC B、AB∥CD C、∠ABD=∠CDB D、∠BAD+∠ADC=180°6. 小明用计算器求了一些正数的平方,记录如下表.
A、AD∥BC B、AB∥CD C、∠ABD=∠CDB D、∠BAD+∠ADC=180°6. 小明用计算器求了一些正数的平方,记录如下表.x
15
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9
16
225
228.01
231.04
234.09
237.16
240.25
243.36
246.49
249.64
252.81
256
下面有四个推断:
① =1.51
②一定有3个整数的算术平方根在15.5~15.6之间
③对于小于15的两个正数,若它们的差等于0.1,则它们的平方的差小于3.01
④16.22比16.12大3.23
所有合理推断的序号是( )
A、①② B、③④ C、①②④ D、①②③④7. 下列推理中,错误的是( )A、∵AB=CD,CD=EF,∴AB=EF B、∵∠α=∠β,∠β=∠γ,∴∠α=∠γ C、∵a∥b,b∥c,∴a∥c D、∵AB⊥EF,EF⊥CD,∴AB⊥CD8. 某班四个小组进行辩论比赛,赛前三位同学预测比赛结果如下:甲说:“第二组得第一,第四组得第三”;
乙说:“第一组得第四,第三组得第二”;
丙说:“第三组得第三,第四组得第一”;
赛后得知,三人各猜对一半,则冠军是( )
A、第一组 B、第二组 C、第三组 D、第四组9. 一同学在n天假期中观察:(1)下了7次雨,在上午或下午
(2)当下午下雨时,上午是晴天
(3)一共有5个下午是晴天
(4)一共有6个上午是晴天
则n最小为( )
A、7 B、9 C、10 D、1110. 在一次400米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )A、甲 B、乙 C、丙 D、丁二、填空题
-
11. 小丽在4张同样的纸片上各写了一个正整数,从中随机抽取2张,并将它们上面的数相加.重复这样做,每次所得的和都是5,6,7,8中的一个数,并且这4个数都能取到.猜猜看,小丽在4张纸片上各写下的数是 .12. 新定义:对非负数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n﹣ ≤ x< n+ 则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若( x-1)= 4,则x的取值范围是9≤x<11;
④当x≥0,m为非负整数时,有(m+2020x)=m+(2020x);
其中正确的结论有(填写所有正确的序号).
13. 如图,长方形是由若干个小长方形和小正方形组成,从面积的角度研究这个图形,可以得到一个数学等式,这个数学等式是 . (用图中的字母表示出来)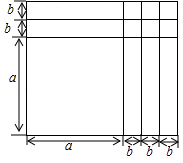 14. 如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 , 破译“正做数学”的真实意思是 .
14. 如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 , 破译“正做数学”的真实意思是 . 15. A、B、C、D、E、F六足球队进行单循环比赛,当比赛到某一天时,统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球,则还没与B队比赛的球队是
15. A、B、C、D、E、F六足球队进行单循环比赛,当比赛到某一天时,统计出A、B、C、D、E、五队已分别比赛了5、4、3、2、1场球,则还没与B队比赛的球队是三、解答题
-
16. 把下面的说理过程补充完整:
已知:如图,在四边形中, , 直线与和的延长线分别交于点 , , 若 , 那么与相等吗?请说明理由.
解: . 理由如下:
因为(已知),
所以 ▲ ▲ ( ),
所以 ▲ ( ),
因为 ▲ (已知),
所以 ▲ ( ),
所以(等量代换).
 17. 补全解题过程.
17. 补全解题过程.已知:如图,于点 , 于点 , .
求证: .
证明:∵ , ,
∴ ▲ .
∴( )(填推理依据).
∴ ▲ ( )(填推理依据).
又∵ ,
∴ ▲ .
∴( )(填推理依据).
 18. 填空并完成以下证明:
18. 填空并完成以下证明:如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.

证明:∵FH⊥AB(已知),
∴∠BHF= ▲ .
∵∠1=∠ACB(已知),
∴DE∥BC,( )
∴∠2= ▲ . ( )
∵∠2=∠3(已知),
∴∠3= ▲ , ( )
∴CD∥FH( )
∴∠BDC=∠BHF= ▲ °,( )
∴CD⊥AB.
四、综合题
-
19. 如图 , , 点A、B在的两条边上运动,与的平分线交于点C.
 (1)、点A、B在运动过程中,的大小会变吗?如果不会,求出的度数;如果会,请说明理由.(2)、如图 , AD是的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,的大小会变吗?如果不会,求出的度数;如果会,请说明理由.(3)、若 , 请直接写出; .20. 已知AB∥CD,线段EF分别与AB,CD相交于点E,F.
(1)、点A、B在运动过程中,的大小会变吗?如果不会,求出的度数;如果会,请说明理由.(2)、如图 , AD是的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,的大小会变吗?如果不会,求出的度数;如果会,请说明理由.(3)、若 , 请直接写出; .20. 已知AB∥CD,线段EF分别与AB,CD相交于点E,F. (1)、请在横线上填上合适的内容,完成下面的解答:
(1)、请在横线上填上合适的内容,完成下面的解答:如图1,当点P在线段EF上时,已知∠A=35°,∠C=62°,求∠APC的度数;
解:过点P作直线PH∥AB,
所以∠A=∠APH,依据是 ▲ ;
因为AB∥CD,PH∥AB,
所以PH∥CD,依据是 ▲ ;
所以∠C=( ),
所以∠APC=( ▲ )+( ▲ )=∠A+∠C=97°.
(2)、当点P,Q在线段EF上移动时(不包括E,F两点):①如图2,∠APQ+∠PQC=∠A+∠C+180°成立吗?请说明理由;
②如图3,∠APM=2∠MPQ,∠CQM=2∠MQP,∠M+∠MPQ+∠PQM=180°,请直接写出∠M,∠A与∠C的数量关系.
21.(1)、世界杯足球小组赛,每组四个队进行单循环比赛.每场比赛胜队得3分,败队记0分,平局时两队各记1分.小组赛全赛完以后,总积分数高的两个队出线进入下一轮比赛.如果总积分相同,则还要按净胜球多少和进球数多少来排序.问一个队至少要积多少分才能保证出线?简述理由.
(2)、在小组赛中,一个队只积3分有可能出线吗?只积2分呢?

