鲁教版（五四制）2022-2023学年度第二学期七年级数学三元一次方程组期中复习

试卷更新日期：2023-04-06 类型：复习试卷

进入出卷网下载

一、单选题

1. 三元一次方程组 ${\begin{array}{l} 3 x - 2 y = 5 ， \\ x + y + z = 2 ， \\ z = 2 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 1 \\ z = 2 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = - 1 \\ z = 2 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 1 \\ z = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 1 \\ z = 2 \end{array}$

查看试题解析
2. 小明到文具店购买文具，他发现若购买4支钢笔、2支铅笔、1支水彩笔需要50元，若购买1支钢笔、3支铅笔、4支水彩笔也正好需要50元，则购买1支钢笔、1支铅笔、1支水彩笔需要（）

A、10元 B、20元 C、30元 D、不能确定

查看试题解析
3. 已知 $x$ 、 $y$ 、 $z$ 是三个非负实数，满足 $3 x + 2 y + z = 5$ ， $x + y - z = 2$ ，若 $S = 2 x + y - z$ ，则 $S$ 的最大值与最小值的和为 $($ $)$

A、5 B、6 C、7 D、8

查看试题解析
4. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6

查看试题解析
5. 解方程组 ${\begin{cases} 3 x - y + 2 z = 3 \\ 2 x + y - 4 z = 11 \\ 7 x + y - 5 z = 1 \end{cases}$ ，若要使运算简便，消元的方法应选取（）

A、先消去x B、先消去y C、先消去z D、以上说法都不对

查看试题解析
6. 已知 ${\begin{cases} 2 x + 3 y = z \\ 3 x + 4 y = 2 z + 6 \end{cases}$ ，且x+y=3，则z的值为（）

A、9 B、-3 C、12 D、不确定

查看试题解析
7. 解三元一次方程组 ${\begin{cases} a + b - c = 1 ① \\ a + 2 b - c = 3 ② \\ 2 a - 3 b + 2 c = 5 ③ \end{cases}$
具体过程如下：

（ 1 ）②-①，得b=2；（2）①×2+③，得4a-2b=7；（3）所以 ${\begin{cases} b = 2 \\ 4 a - 2 b = 7 \end{cases}$ ；（4）把b=2代入4a-2b=7，得4a-2×2=7（以下求解过程略）其中开始出现错误的一步是（）

A、（1） B、（2） C、（3） D、（4）

查看试题解析
8. 有甲、乙、丙三种商品，如果购买3件甲商品、2件乙商品、1件丙商品共需315元，购买1件甲商品、2件乙商品、3件丙商品共需285元，那么购买甲、乙、丙三种商品各一件共需（）

A、50元 B、100元 C、150元 D、200元

查看试题解析
9. 三元一次方程组 ${\begin{array}{l} x - y = 1 \\ y - z = 1 \\ x + z = 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \\ z = 4 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 4 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 4 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 3 \\ z = 2 \end{array}$

查看试题解析
10. 甲、乙、丙三种商品，若购买甲2件、乙4件、丙3件，共需220元钱，购甲3件、乙1件、丙2件共需235元钱，那么购甲、乙、丙三种商品各一件共需（）

A、85元 B、89元 C、90元 D、91元

查看试题解析

二、填空题

11. 若 ${\begin{cases} x + y = 27 \\ y + z = 33 \\ z + x = 30 \end{cases}$ ，则代数式x+y+z的值为．

查看试题解析
12. 重庆一中趣味数学社团在社团活动日举办了知识竞答挑战赛.比赛共设置有A、B、C三关，每关设有若干问题，且每关的每个问题分值相同.参赛选手需回答完所有试题，答对得分，答错不扣分.甲、乙、丙三人作答完毕后，结果如下：甲在A、B、C三个关中回答正确的问题数目之比为 $2 ： 1 ： 1$ ，在A关的得分占甲总得分的75%；乙在A、B、C三个关中回答正确的问题数目之比为 $2 ： 5 ： 2$ ，在B关的得分占乙总得分的 $\frac{1}{3}$ ；丙在A关回答正确的问题数目是甲、乙在A关回答正确的问题数目之和的一半，丙在B关回答正确的问题数目比乙在B关回答正确的问题数目少 $\frac{2}{5}$ ，丙与甲在C关回答正确的数目相同，若甲、乙两人的总得分之比为 $48 ： 25$ ，则乙、丙两人的总得分之比为.

查看试题解析
13. 实数x，y，z满足2x+y-3z=5，x+2y+z=-4，请用含x的代数式表示z，即.

查看试题解析
14. “端午节”是我国的传统佳节，民间历来有吃粽子的习俗.某超市准备了515个豆沙粽，525个火腿粽和若干个腊肉棕，将这些粽子分成了A，B，C三类礼品盒进行包装.A类礼品盒里有4个豆沙粽，4个火腿粽和6个腊肉粽；B类礼品盒里有3个豆沙粽，5个火腿粽和6个腊肉粽；C类礼品盒里有6个豆沙粽，4个火腿粽和4个腊肉粽.已知A，B，C三类礼品盒的数量都为正整数，并且A类礼品盒少于44盒，B类礼品盒少于49盒.如果所有礼品盒里的腊肉粽的总个数为m，则m=

查看试题解析
15. 如图，在正方形 $A B C D$ 的每个顶点上写一个数，然后把它的每条边的两个端点上的数加起来，将结果写在这条边上，若 $A B$ 边上的数字是3， $B C$ 边上的数字是7， $C D$ 边上的数字是10，则 $A D$ 边上的数字是.

查看试题解析

三、解答题

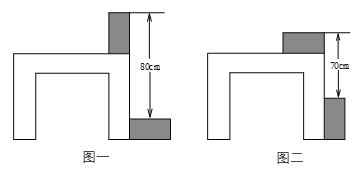
16. 在解方程组 ${\begin{array}{l} a x - b y = 13 \\ c x - y = 4 \end{array}$ 时，甲同学因看错了b的符号，从而求得解为 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ，乙同学因看漏了c，从而求得解为 ${\begin{matrix} x = 5 \\ y = 1 \end{matrix}$ ，试求(b＋c)^a的值．

查看试题解析
17. 购买铅笔7支，作业本3本，圆珠笔1支共需6元；购买铅笔10支，作业本4本，圆珠笔1支共需8元.求购买铅笔11支，作业本5本，圆珠笔2支共需多少元.

查看试题解析
18. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.

查看试题解析

四、综合题

19. 已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ ，求 $- 2 x + y + 4 z$ 的值.
小明凑出“ $- 2 x + y + 4 z = 2 \times (x + 2 y + 3 z) + (- 1) \times (4 x + 3 y + 2 z) = 20 - 15 = 5$ ”，虽然问题获得解决，但他觉得凑数字很辛苦！他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设 $- 2 x + y + 4 z = m (x + 2 y + 3 z) + n (4 x + 3 y + 2 z)$ ，对照方程两边各项的系数可列出方程组 ${\begin{array}{l} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{array}$ 它的解就是你凑的数！

(1)、根据丁老师的提示，已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 3 \\ 4 x + 3 y + 2 z = 7 \end{array}$ ，求 $2 x + 5 y + 8 z$ 的值.

(2)、已知 $2 a - b + k c = 4$ ，且 $a + 3 b + 2 c = - 2$ ，当k为时， $8 a + 3 b - 2 c$ 为定值，此定值是.（直接写出结果）

查看试题解析
20. 在等式y=ax²+bx+c中，当x=-1时，y=4；当x=2时，y=4；当x=1时，y=2.

(1)、求a，b，c的值；

(2)、当x=-2时，求y的值.

查看试题解析
21. 对于一个三位数 $n$ ，如果 $n$ 满足：它的百位数字、十位数字之和与个位数字的差等于8，那么称这个数 $n$ 为“快乐数”.例如： $n_{1} = 934$ ， $∵ 9 + 3 - 4 = 8$ ， $∴ 934$ 是“快乐数”； $n_{2} = 701$ ， $∵ 7 + 0 - 1 = 6$ ， $∴ 701$ 不是“快乐数”.

(1)、判断844，735是否为“快乐数”？并说明理由；

(2)、若将一个“快乐数” $m$ 的个位数的3倍放到百位，原来的百位数变成十位数，原来的十位数变成个位数，得到一个新的三位数 $t$ （例如：若 $m = 642$ ，则 $t = 664$ ），若 $t$ 也是一个“快乐数”，求满足条件的所有 $m$ 的值.

查看试题解析
22. 【信息阅读】
有些问题，所要求的结果往往不是某一个量的值，而是某些式子或问题的整体值.
如下面的问题：
问题：已知实数x，y同时满足3x- y =5①，和2x+3y =7②．求代数式7x+5y的值.
思路1：将①和②联立组成方程组，先求得x、y的值后，再代入7x +5y求值.
思路2：为降低运算量，由①+②×2，可直接得出7x+5y = 19．这样的解题思路即为整体思想.
【问题解决】

(1)、已知方程组 ${\begin{cases} 3 x + 2 y = 7 \\ 2 x + 3 y = 3 \end{cases}$ ，则x- y =；

(2)、若购买13支铅笔、5块橡皮、3本日记本共需33元；若购买25支铅笔、9块橡皮、3本日记本共需55元，求购买1支铅笔、1块橡皮、3本日记本共需多少元?

查看试题解析
23. 水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如表所示：（假设每辆车均满载）
车型
甲
乙
丙
汽车运载量（吨/辆）
5
8
10
汽车运费（元/辆）
400
500
600

(1)、若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，市场可以调用甲、乙、丙三种车型参与运送（每种车型至少1辆），已知它们的总辆数为16辆，如何安排车辆运送使总运费最省？

查看试题解析

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	400	500	600

鲁教版（五四制）2022-2023学年度第二学期七年级数学 三元一次方程组 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期七年级数学三元一次方程组期中复习