云南省玉溪市2023届高三数学毕业生第一次教学质量检测试卷
试卷更新日期:2023-04-06 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、(-2,2) B、[0,3) C、(-2,3) D、(-2,3]2. 如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数(其中)为“等部复数”,则复数在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在扇形COD中 , . 设向量 , , 则( )A、-4 B、4 C、-6 D、64. 如图是某灯具厂生产的一批不倒翁型台灯外形,它由一个圆锥和一个半球组合而成,圆锥的高是0.4m,底面直径和球的直径都是0.6m,现对这个台灯表面涂胶,如果每平方米需要涂200克,则共需涂胶( )克(精确到个位数)
 A、176 B、207 C、239 D、2705. 已知奇函数图像的相邻两个对称中心间的距离为2π,将的图像向右平移个单位得函数的图像,则的图像( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称6. 若 , 则在“函数的定义域为”的条件下,“函数为奇函数”的概率为( )A、 B、 C、 D、7. 已知展开式中x的系数为q,空间有q个点,其中任何四点不共面,这q个点可以确定的直线条数为m,以这q个点中的某些点为顶点可以确定的三角形个数为n,以这q个点中的某些点为顶点可以确定的四面体个数为p,则( )A、2022 B、2023 C、40 D、508. 已知 , , , 则( )A、 B、 C、 D、
A、176 B、207 C、239 D、2705. 已知奇函数图像的相邻两个对称中心间的距离为2π,将的图像向右平移个单位得函数的图像,则的图像( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称6. 若 , 则在“函数的定义域为”的条件下,“函数为奇函数”的概率为( )A、 B、 C、 D、7. 已知展开式中x的系数为q,空间有q个点,其中任何四点不共面,这q个点可以确定的直线条数为m,以这q个点中的某些点为顶点可以确定的三角形个数为n,以这q个点中的某些点为顶点可以确定的四面体个数为p,则( )A、2022 B、2023 C、40 D、508. 已知 , , , 则( )A、 B、 C、 D、二、多选题
-
9. 已知双曲线C过点且渐近线方程为 , 则下列结论正确的是( )A、C的方程为 B、C的离心率为 C、曲线经过C的一个焦点 D、C的焦点到渐近线的距离为110. 已知 , 且则下列结论一定正确的有( )A、 B、 C、ab有最大值4 D、有最小值911. 已知函数 , 则下列结论正确的有( )A、 B、函数图象关于直线对称 C、函数的值域为 D、若函数有四个零点,则实数的取值范围是12. 在棱长为1的正方体 中, 为底面的中心,是棱 上一点,且 , , 为线段 的中点,给出下列命题,其中正确的是( )
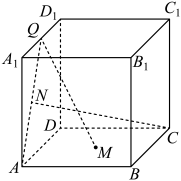 A、 与 共面; B、三棱锥 的体积跟的取值无关; C、当时, ; D、当时,过 , , 三点的平面截正方体所得截面的周长为 .
A、 与 共面; B、三棱锥 的体积跟的取值无关; C、当时, ; D、当时,过 , , 三点的平面截正方体所得截面的周长为 .三、填空题
-
13. 已知函数的图象在处的切线的倾斜角为α,则 .14. 已知随机变量 , 若 , 则p= .15. 已知直线与圆C:相交于点A,B,若是正三角形,则实数16. 已知 , 分别是椭圆的左、右焦点, , 是椭圆与抛物线的公共点, , 关于轴对称且位于轴右侧, , 则椭圆的离心率的最大值为 .
四、解答题
-
17. 在① , ②这两个条件中选择一个补充在下面的问题中,然后求解.
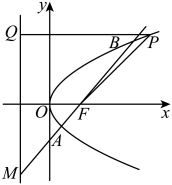
设等差数列的公差为 , 前n项和为 , 等比数列的公比为q.已知 , , ____.(说明:只需选择一个条件填入求解,如果两个都选择并求解的,只按选择的第一种情形评分)
(1)、请写出你的选择,并求数列和的通项公式;(2)、若数列满足 , 设的前n项和为 , 求证: .18. 在△ABC中,角A,B,C的对边长依次是a,b,c, , .(1)、求角B的大小;(2)、当△ABC面积最大时,求∠BAC的平分线AD的长.19. 某地A,B,C,D四个商场均销售同一型号的冰箱,经统计,2022年10月份这四个商场购进和销售该型号冰箱的台数如下表(单位:十台):A商场
B商场
C商场
D商场
购讲该型冰箱数x
3
4
5
6
销售该型冰箱数y
2.5
3
4
4.5
参考公式:回归方程中斜率和截距的最小二乘估计公式分别为 , .
(1)、已知可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;(2)、假设每台冰箱的售价均定为4000元.若进入A商场的甲、乙两位顾客购买这种冰箱的概率分别为p, , 且甲乙是否购买冰箱互不影响,若两人购买冰箱总金额的期望不超过6000元,求p的取值范围.20. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形, , , M,N分别是线段AB,PC的中点.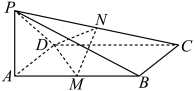 (1)、求证:MN平面PAD;(2)、在线段CD上是否存在一点Q,使得直线NQ与平面DMN所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.
(1)、求证:MN平面PAD;(2)、在线段CD上是否存在一点Q,使得直线NQ与平面DMN所成角的正弦值为?若存在,求出的值;若不存在,请说明理由.