天津市和平区2023届高三下学期数学一模试卷
试卷更新日期:2023-04-06 类型:高考模拟
一、单选题
-
1. 已知全集 , 则中元素个数为( )A、3个 B、4个 C、5个 D、6个2. 已知a是实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 函数y=lncosx(-<x)的图象是( )A、
 B、
B、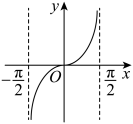 C、
C、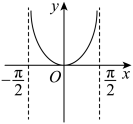 D、
D、 4. 某城市在创建文明城市的活动中,为了解居民对“创建文明城市”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为100的样本,发现数据均在内.现将这些分数分成6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示观察图形,则下列说法错误的是( )
4. 某城市在创建文明城市的活动中,为了解居民对“创建文明城市”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为100的样本,发现数据均在内.现将这些分数分成6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示观察图形,则下列说法错误的是( ) A、频率分布直方图中第三组的频数为15人 B、根据频率分布直方图估计样本的众数为75分 C、根据频率分布直方图估计样本的中位数为75分 D、根据频率分布直方图估计样本的平均数为75分5. 已知 , 则的大小关系为( )A、 B、 C、 D、6. 将函数图象上所有点的横坐标缩短为原来的 , 纵坐标不变,再将所得的图象向右平移个单位长度,得到函数的图象,则( )A、的最小正周期为 B、的图象关于直线对称 C、在上单调递增 D、的图像关于点对称7. 抛物线的焦点为 , 其准线与双曲线的渐近线相交于两点,若的周长为 , 则( )A、2 B、 C、8 D、48. 为庆祝国庆,立德中学将举行全校师生游园活动,其中有一游戏项目是夹弹珠.如图,四个半径都是1cm的玻璃弹珠放在一个半球面形状的容器中,每颗弹珠的顶端恰好与容器的上沿处于同一水平面,则这个容器的容积是( )
A、频率分布直方图中第三组的频数为15人 B、根据频率分布直方图估计样本的众数为75分 C、根据频率分布直方图估计样本的中位数为75分 D、根据频率分布直方图估计样本的平均数为75分5. 已知 , 则的大小关系为( )A、 B、 C、 D、6. 将函数图象上所有点的横坐标缩短为原来的 , 纵坐标不变,再将所得的图象向右平移个单位长度,得到函数的图象,则( )A、的最小正周期为 B、的图象关于直线对称 C、在上单调递增 D、的图像关于点对称7. 抛物线的焦点为 , 其准线与双曲线的渐近线相交于两点,若的周长为 , 则( )A、2 B、 C、8 D、48. 为庆祝国庆,立德中学将举行全校师生游园活动,其中有一游戏项目是夹弹珠.如图,四个半径都是1cm的玻璃弹珠放在一个半球面形状的容器中,每颗弹珠的顶端恰好与容器的上沿处于同一水平面,则这个容器的容积是( ) A、 B、 C、 D、9. 已知函数 ,设方程 的四个实根从小到大依次为 ,对于满足条件的任意一组实根,下列判断中一定成立的是( )A、 B、 C、 D、
A、 B、 C、 D、9. 已知函数 ,设方程 的四个实根从小到大依次为 ,对于满足条件的任意一组实根,下列判断中一定成立的是( )A、 B、 C、 D、二、填空题
-
10. 设为虚数单位,复数.11. 的展开式中常数项为.12. 直线与圆交 , 两点,若为等边三角形,则的值为 .13. 先后掷两次骰子(骰子的六个面上的点数分别是1、2、3、4、5、6),落在水平桌面后,记正面朝上的点数分别为x、y,记事件A为“为偶数”,事件B为“x、y中有偶数且”,则概率 , .14. 若实数x、y满足 , 则的最大值是 .15. 已知四边形 , 且 , 点为线段 , 上一点,且 , 则 , 过作∥交于点 , 则.
三、解答题
-
16. 已知的内角的对边分别为 , 且.(1)、求的大小:(2)、若 ,
(i)求的面积;
(ii)求.
17. 在如图所示的几何体中,平面平面;是的中点. (1)、求证:;(2)、求直线与平面所成角的正弦值;(3)、求平面与平面的夹角的余弦值.18. 已知数列为首项的等比数列,且成等差数列;数列为首项的单调递增的等差数列,数列的前项和为 , 且成等比数列.(1)、求数列的通项公式;(2)、求;(3)、数列满足 , 记和分别为和的前项和,证明:.
(1)、求证:;(2)、求直线与平面所成角的正弦值;(3)、求平面与平面的夹角的余弦值.18. 已知数列为首项的等比数列,且成等差数列;数列为首项的单调递增的等差数列,数列的前项和为 , 且成等比数列.(1)、求数列的通项公式;(2)、求;(3)、数列满足 , 记和分别为和的前项和,证明:.