吉林省长春市吉大附中2021-2022学年九年级下学期一模数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 下列各数中,最大的数是( )A、-2 B、0 C、3 D、62. 据省统计局公布的数据,2021年上半年某省统筹疫情防控和经济社会发展成效持续显现,农村居民人均可支配收入达到10010元,高出全国平均水平762元,这里“10010”用科学记数法表示( )A、 B、 C、 D、3. 如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
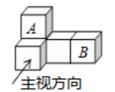 A、左视图会发生改变,其他视图不变 B、俯视图会发生改变,其他视图不变 C、主视图会发生改变,其他视图不变 D、三种视图都会发生改变4. 如图,AB为⊙O的直径,点C、D在⊙O上,若∠BCD=30°,则∠ABD的大小为( )
A、左视图会发生改变,其他视图不变 B、俯视图会发生改变,其他视图不变 C、主视图会发生改变,其他视图不变 D、三种视图都会发生改变4. 如图,AB为⊙O的直径,点C、D在⊙O上,若∠BCD=30°,则∠ABD的大小为( ) A、60° B、50° C、40° D、20°5. 若关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则常数c的值为( )A、±4 B、4 C、±16 D、166. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、
A、60° B、50° C、40° D、20°5. 若关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则常数c的值为( )A、±4 B、4 C、±16 D、166. 如图,在△ABC中,∠C=90°,AC>BC.用直尺和圆规在边AC上确定一点P,使点P到AB、BC的距离相等,则符合要求的作图痕迹( )A、 B、
B、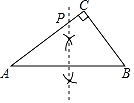 C、
C、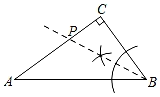 D、
D、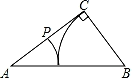 7. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).
7. 如图是某商场营业大厅自动扶梯的示意图.自动扶梯 的倾斜角为 ,大厅两层之间的距离 为6米,则自动扶梯 的长约为( )( ).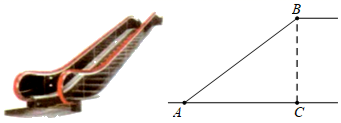 A、7.5米 B、8米 C、9米 D、10米8. 如图,直线交y轴于点A,交双曲线于点B,将直线向下平移2个单位长度后与y轴交于点C,交双曲线于点D,若 , 则n的值( )
A、7.5米 B、8米 C、9米 D、10米8. 如图,直线交y轴于点A,交双曲线于点B,将直线向下平移2个单位长度后与y轴交于点C,交双曲线于点D,若 , 则n的值( ) A、4 B、3 C、2 D、5
A、4 B、3 C、2 D、5二、填空题
-
9. 分解因式: .10. “如果两直线平行,那么同旁内角相等”是命题.(填“真”或“假”)11. 将直角三角形纸片和矩形纸片按如图方式折叠放在一起,若 , 则 .
 12. 如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当 OM=cm时,⊙M与OA相切.
12. 如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M,当 OM=cm时,⊙M与OA相切. 13. 如图所示,把一张矩形的纸片按图示对折两次,然后剪下一部分,若得到一个钝角为120°的菱形,则剪口与第二次折痕所成角的度数应为 .
13. 如图所示,把一张矩形的纸片按图示对折两次,然后剪下一部分,若得到一个钝角为120°的菱形,则剪口与第二次折痕所成角的度数应为 . 14. 已知函数 , 当时, , 则m的取值范围是 .
14. 已知函数 , 当时, , 则m的取值范围是 .三、解答题
-
15. 求值: .16. 图①、图②均为 4×4 的正方形网格,线段 AB、BC 的端点均在格点上,按要求在图①、图②中作图并计算其面积.

 (1)、在图①中画一个四边形 ABCD,点D在格点上 , 使四边形 ABCD 有一组对角相等,并求 .(2)、在图②中画一个四边形 ABCE,点E在格点上 , 使四边形 ABCE 有一组对角互补,并求 .17. 先化简,再求值:( +1)÷ ,其中a=﹣4.18. 如图,在△ABC中,∠C=90°,点O为AB上一点,以OA为半径的⊙O与BC相切于点D,连结AD,过D作DE⊥AB,垂足为点E.
(1)、在图①中画一个四边形 ABCD,点D在格点上 , 使四边形 ABCD 有一组对角相等,并求 .(2)、在图②中画一个四边形 ABCE,点E在格点上 , 使四边形 ABCE 有一组对角互补,并求 .17. 先化简,再求值:( +1)÷ ,其中a=﹣4.18. 如图,在△ABC中,∠C=90°,点O为AB上一点,以OA为半径的⊙O与BC相切于点D,连结AD,过D作DE⊥AB,垂足为点E. (1)、求证:AD平分∠CAB.(2)、若AB=20,且AE:EB=3:2,则⊙O的半径为 .19. 2020年11月19日,长春发生了罕见的冻雨灾害,市政清洁队一个小分队承担着2100米长的道路冰雪清理任务.为了提高清理进度,在清理了300米后增加了人数和设备,清理效率是原来的4倍,结果共用了5小时就完成了清理任务求原来每小时清理的长度.20. 为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列可题:
(1)、求证:AD平分∠CAB.(2)、若AB=20,且AE:EB=3:2,则⊙O的半径为 .19. 2020年11月19日,长春发生了罕见的冻雨灾害,市政清洁队一个小分队承担着2100米长的道路冰雪清理任务.为了提高清理进度,在清理了300米后增加了人数和设备,清理效率是原来的4倍,结果共用了5小时就完成了清理任务求原来每小时清理的长度.20. 为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组(从左到右的顺序).统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列可题: (1)、本次调查共随机抽取了该年级名学生,并将频数分布直方图补充完整;(2)、估计该年级1500名考生中,考试成绩120分以上(含120分)学生有名;(3)、扇形统计图中,第二组所占圆心角的度数为 .(4)、如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生好是一名女生和一名男生的概率.21. 一艘轮船在航行中遇到暗礁船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,修船过程中进水和排水速度不变,修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽.设轮船触礁后船舱内积水量为 ,时间为 ,y与x之间的函数图象如图所示.
(1)、本次调查共随机抽取了该年级名学生,并将频数分布直方图补充完整;(2)、估计该年级1500名考生中,考试成绩120分以上(含120分)学生有名;(3)、扇形统计图中,第二组所占圆心角的度数为 .(4)、如果第一组(75~90)中只有一名是女生,第五组(135~150)中只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想.请你用列表或画树状图的方法求出所选两名学生好是一名女生和一名男生的概率.21. 一艘轮船在航行中遇到暗礁船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,修船过程中进水和排水速度不变,修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽.设轮船触礁后船舱内积水量为 ,时间为 ,y与x之间的函数图象如图所示. (1)、修船过程中排水速度为 ,a的值为 .(2)、求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.(3)、当船内积水量是船内最高积水量的 时,直接写出x的值.22.
(1)、修船过程中排水速度为 ,a的值为 .(2)、求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.(3)、当船内积水量是船内最高积水量的 时,直接写出x的值.22.
【感知】小亮遇到了这样一道题:已知如图①在中,在上,E在的延长上,交于点F,且 , 求证:.
小亮仔细分析了题中的已知条件后,如图②过D点作交于G,进而解决了该问题.(不需要证明)
(1)、【探究】如图③,在四边形中, , 为边的中点,与的延长线交于点F,试探究线段与之间的数量关系,并证明你的结论.(2)、【应用】如图④,在正方形中,E为边的中点,G、F分别为 , 边上的点,若=1,= , ∠=90°,则的长为.23. 如图,在中, , , , D为AB的中点,动点P从点A出发以每秒4个单位向终点B匀速运动(点P不与A、D、B重合),过点P作AB的垂线交折线于点Q.以PQ、PD为邻边构造矩形PQMD.设矩形PQMD与重叠部分图形的面积为S,点P的运动时间为t秒. (1)、直接写出PQ的长(用含t的代数式表示).(2)、当点M落在的边上时,求t的值.(3)、当矩形PQMD与重叠部分图形为矩形时,求S与t的函数关系式.并写出t的取值范围.(4)、沿直线CD将矩形PQMD剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,请直接写出所有符合条件的t的值.24. 在平面直角坐标系中,把函数 ( 、 为常数)的图象记为 .(1)、求 与 轴交点的坐标.(2)、当 时, 与 只有一个交点,求 的值.(3)、①设 ,若点 在 上,则点 必在 上,且 过点 ,求 的函数表达式.
(1)、直接写出PQ的长(用含t的代数式表示).(2)、当点M落在的边上时,求t的值.(3)、当矩形PQMD与重叠部分图形为矩形时,求S与t的函数关系式.并写出t的取值范围.(4)、沿直线CD将矩形PQMD剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,请直接写出所有符合条件的t的值.24. 在平面直角坐标系中,把函数 ( 、 为常数)的图象记为 .(1)、求 与 轴交点的坐标.(2)、当 时, 与 只有一个交点,求 的值.(3)、①设 ,若点 在 上,则点 必在 上,且 过点 ,求 的函数表达式.②点 、 是①中函数图象上的两点,比较 与 的大小.
③点 、 是①中函数图象上的两点,比较 与 的大小.
(4)、矩形 四个顶点的坐标分别为 、 、 、 ,当 时,函数 ( )的图象在矩形 内部的部分均为自左向右下降时,直接写出 的取值范围.