吉林省长春市新区2022年中考数学二模试题

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数a在数轴上的对应点的位置如图所示，若实数b满足 $a + b > 0$ ，则b的值可以是（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
2. 2021年2月24日6时29分，我国自主研制的首个火星探测器“天问一号”成功实施第三次近火制动，进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道．将59000用科学记数法表示应为（）

A、 $0.59 \times 10^{5}$ B、 $5.9 \times 10^{5}$ C、 $5.9 \times 10^{4}$ D、 $5.9 \times 10^{3}$

查看试题解析
3. 如图是某几何体的视图，该几何体是（）

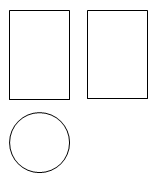A、圆柱 B、球 C、三棱柱 D、长方体

查看试题解析
4. 如图， $A B / / C D ， ∠ A = 100 ° ， ∠ B C D = 50 ° ， ∠ A C B$ 的度数为（）

A、 $25 °$ B、 $30 °$ C、 $45 °$ D、 $50 °$

查看试题解析
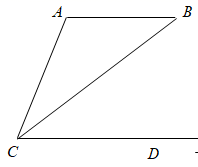5. 已知关于x的一元二次方程 $x^{2} + m x + m - 1 = 0$ 有两个不相等的实数根，下列结论正确的是（）

A、 $m \neq 2$ B、 $m > 2$ C、 $m \geq 2$ D、 $m < 2$

查看试题解析
6. 如果 $a - b = 2$ ，那么代数式 $(\frac{a^{2} + b^{2}}{a} - 2 b) \cdot \frac{a}{a - b}$ 的值是（）

A、2 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
7. 如图，已知直线l₁⊥l₂ ，且在某平面直角坐标系中， x轴∥l₁ ， y轴∥l₂ ，若点A的坐标为(-1，2)，点B的坐标为(2，-1)，则点C在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 在平面直角坐标系中，一次函数y＝x+a（a≠0）的图象与y轴交于点A．过点B（0，2a）且平行于x轴的直线与一次函数y＝x+a（a≠0）的图象、反比例函数y＝ $\frac{3 a}{x}$ 的图象分别交于点C、D．若CD≥BD，则a的取值范围是（　　）

A、a＜0 B、a≥3 C、a＜0或a≥3 D、0＜a≤3

查看试题解析

二、填空题

9. 因式分解： $a^{2} b - b =$ ．

查看试题解析
10. 若 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
11. 若正多边形的一个外角为30°，则这个多边形为正边形．

查看试题解析
12. 图1中的直角三角形有一条直角边长为3，将四个图1中的直角三角形分别拼成如图2，图3所示的正方形，其中阴影部分的面积分别记为 $S_{1} ， S_{2}$ ，则 $S_{1} - S_{2}$ 的值为．

查看试题解析
13. 如图，AB为⊙O的直径，点C在AB的延长线上，CD与⊙O相切于D，过点B作BE $∥$ CD交⊙O于点E，连接AD，AE，且∠EAD＝22.5°．若BC＝2 $\sqrt{2}$ -2，则BE的长为．

查看试题解析
14. 图1是一个坡度为1：2的斜坡的横截面，斜坡顶端B与地面的距离BC为2.5米，为了对这个斜坡上的绿地进行喷灌，在斜坡底端安装了一个喷头A，喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分，设喷出水珠的竖直高度为y（单位：米）（水珠的竖直高度是指水珠与地面的距离），水珠与喷头A的水平距离为x（单位：米），图2记录了y与x的相关数据，则y与x的函数关系式为．

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{4})}^{- 1} + 2 \cos 45 ° - | - \sqrt{2} | + {(2021 - π)}^{0}$ ．

查看试题解析
16. 盒中有2枚白色棋子和2枚黑色棋子，这四枚棋子除颜色外无其他差别，从中一次，摸出两枚棋子，用树状图（或列表法）求摸出的两枚棋子一黑一白的概率．

查看试题解析
17. 《孙子算经》是中国南北朝时期重要的数学专著，其中包含了“鸡兔同笼”、“物不知数”等许多有趣的数学问题，《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”其译文为：“用一根绳子去量一根长木，绳子还剩余4.5尺，将绳子对折再量长木，长木还剩余1尺，问木长多少尺？”请解答《孙子算经》中的这道题．

查看试题解析
18. 图①、图②、图③均是5×5的正方形网格，每个小正方形的顶点称为格点．△ABC的顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，并保留适当的作图痕迹．

(1)、在图①中的BC边上确定一点D，使得AD平分△ABC的面积．

(2)、在图②中的BC边上确定一点E，使得AE平分∠BAC．

(3)、在图③中的AC边上确定一点F，使得BF平分△ABC的周长．

查看试题解析
19. 品味诗词之美，传承中华文明，央视节目《中国诗词大会》备受大众欢迎，节目规则如下：由100位诗词爱好者组成的百人团与挑战者共同答题，每位挑战者最多可答五轮题，每轮比赛答题时，如挑战者答对，则百人团答错的人数即为选手该轮得分；如挑战者答错，则该轮不得分，且停止答题．每轮比赛的得分之和即为挑战者的总得分，现有甲、乙、丙三人作为挑战者参加节目答题，相关信息如下：
a．甲、乙两人参加比赛的得分统计图如图1，每个点的横坐标与纵坐标分别表示甲、乙二人在相同轮次的得分；

b．丙参加比赛的得分统计图如图2；

根据以上信息，回答下列问题：

(1)、已知点A的坐标为（26，18），则此轮比赛中：乙的得分为，与乙同场答题的百人团中，有人答对；

(2)、这五轮比赛中，甲得分高于乙得分的比赛共有轮；甲、乙、丙三人中总得分最低的为；

(3)、设甲参加的第一轮至第五轮比赛时百人团答对人数的方差为 $s_{1}^{2}$ ，乙参加的第一轮至第五轮比赛时百人团答对人数的方差为 $s_{2}^{2}$ ，则 $s_{1}^{2}$ $s_{2}^{2}$ ．（填“＞”，“＜”或“＝”）

查看试题解析
20. 如图，在矩形ABCD中，对角线AC，BD相交于点O，过点C作CE $∥$ BD，交AD的延长线于点E．

(1)、求证：∠ACD＝∠ECD；

(2)、连接OE，若AB＝1，tan∠ACD＝2．求OE的长．

查看试题解析

21. 小明根据学习函数的经验，对函数y＝-|x|+3的图象与性质进行了探究．下面是小明的探究过程，请你解决相关问题．

(1)、如表y与x的几组对应值：

X	…	-4	-3	-2	-1	0	1	2	3	4	…
Y	…	-1	0	1	2	3	2	1	a	-1	…

①a＝；

②若A（b，-7）为该函数图象上的点，则b＝；

(2)、如图，在平面直角坐标系中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象：

①该函数有（填“最大值”或“最小值”），并写出这个值为；

②求出函数图象与坐标轴在第二象限内所围成的图形的面积．

查看试题解析

22.

(1)、【问题原型】如图①，在等边三角形ABC内部有一点P，PA＝2，PB＝ $\sqrt{3}$ ， PC＝1，求∠BPC的度数，解决方法：将线段BP绕点B逆时针旋转60°得到线段BP'，连结AP'、PP'易证△BPC≌△BP'A，则∠BPC＝度．

(2)、【类比迁移】如图②，在正方形ABCD内有一点P，且PA＝ $\sqrt{10}$ ， PB＝2，PC＝ $\sqrt{2}$ ．
∠BPC＝度．

(3)、求正方形ABCD的边长．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $s i n A = \frac{3}{5}$ ．点P从点A出发，以每秒4个单位长度的速度向终点B匀速运动，过点P作 $P D ⊥ A B$ 交折线 $A C$ ， $C B$ 于点D，连结 $B D$ ，将 $△ D B P$ 绕点D逆时针旋转 $90 °$ 得到 $△ D E F$ ．设点P的运动时间为t（秒）．

(1)、用含t的代数式表示线段 $P D$ 的长．

(2)、当点E落在 $A B$ 边上时，求 $A D$ 的长．

(3)、当点F在 $△ A B C$ 内部时，求t的取值范围．

(4)、当线段 $D P$ 将 $△ A B C$ 的面积分成 $1 ： 2$ 的两部分时，直接写出t的值．

查看试题解析
24. 在平面直角坐标系中，抛物线y＝x²-2mx+m²与y轴的交点为A，过点A作直线l垂直于y轴．

(1)、求抛物线的对称轴（用含m的式子表示）；

(2)、将抛物线在y轴右侧的部分沿直线l翻折，其余部分保持不变，组成图形G，点M（x₁ ， y₁），N（x₂ ， y₂）为图形G上任意两点．
①当m＝0时，若x₁＜x₂ ，判断y₁与y₂的大小关系，并说明理由；
②若对于x₁＝m-1，x₂＝m+1，都有y₁＞y₂ ，求m的取值范围；

(3)、当图象G与直线y＝m+2恰好有3个公共点时，直接写出m的取值范围．

查看试题解析