吉林省长春市绿园区2022年中考二模数学试题
试卷更新日期:2023-04-06 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 根据国家统计局数据显示,我国冰雪运动参与人数达到346000000人.数据346000000用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的几何体是由6个大小相同的小正方体组成,它的主视图为( )
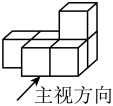 A、
A、 B、
B、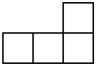 C、
C、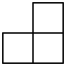 D、
D、 4. 一元二次方程2x2﹣3x﹣4=0的根的情况是( )A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根5. 如图,一棵大树被台风拦腰刮断,树根A到刮断点的距离是4米,折断部分与地面成的夹角,那么原来这棵树的高度是( )
4. 一元二次方程2x2﹣3x﹣4=0的根的情况是( )A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根5. 如图,一棵大树被台风拦腰刮断,树根A到刮断点的距离是4米,折断部分与地面成的夹角,那么原来这棵树的高度是( )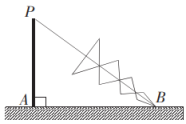 A、米 B、米 C、米 D、米6. 如图,AB是⊙O的直径,点C在AB延长线上,CD与⊙O相切于点D,连接AD,若∠ACD=20°,则∠CAD的度数等于( )
A、米 B、米 C、米 D、米6. 如图,AB是⊙O的直径,点C在AB延长线上,CD与⊙O相切于点D,连接AD,若∠ACD=20°,则∠CAD的度数等于( )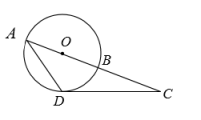 A、20° B、25° C、35° D、45°7. 在中, , , , 用无刻度的直尺和圆规在边上找一点 , 使 , 下列作法错误的是( )A、
A、20° B、25° C、35° D、45°7. 在中, , , , 用无刻度的直尺和圆规在边上找一点 , 使 , 下列作法错误的是( )A、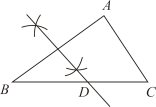 B、
B、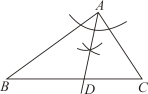 C、
C、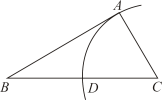 D、
D、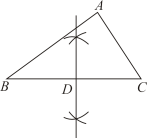 8. 如图,在平面直角坐标系中,矩形的边、分别在y轴和x轴上,已知对角线 . . F是边上一点,过点F的反比例函数的图象与边交于点E,若将沿翻折后,点C恰好落在上的点M处,则k的值为( )
8. 如图,在平面直角坐标系中,矩形的边、分别在y轴和x轴上,已知对角线 . . F是边上一点,过点F的反比例函数的图象与边交于点E,若将沿翻折后,点C恰好落在上的点M处,则k的值为( )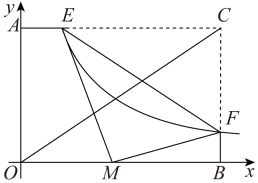 A、2 B、 C、3 D、
A、2 B、 C、3 D、二、填空题
-
9. 分解因式: .10. 若点P(3a-9,1-a)在第三象限内,且a为整数,则a的值是.11. 如图,把三角尺的直角顶点放在直线b上, , 若 , 则°.
 12. 如图,若的半径为 , , , , 则的长为 .
12. 如图,若的半径为 , , , , 则的长为 .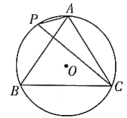 13. 如图,在平面直角坐标系中,点A在第一象限,连结 , 过点A作轴于点B, , , 把绕点O逆时针旋转后,得到 , 则点的坐标为 .
13. 如图,在平面直角坐标系中,点A在第一象限,连结 , 过点A作轴于点B, , , 把绕点O逆时针旋转后,得到 , 则点的坐标为 .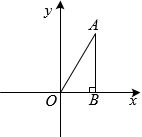 14. 如图,在平面直角坐标系中,抛物线与轴正半轴交于点 . 以为边在轴上方作正方形 , 延长交抛物线于点 , 再以为边向上作正方形 . 则点的坐标是 .
14. 如图,在平面直角坐标系中,抛物线与轴正半轴交于点 . 以为边在轴上方作正方形 , 延长交抛物线于点 , 再以为边向上作正方形 . 则点的坐标是 .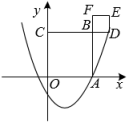
三、解答题
-
15. 先化简,再求值: ,其中 .16. 现有三张不透明的牌,正面分别标有数字2、3、5,这三张牌除正面数字不同外其余均相同,将三张牌背面朝上,洗匀后放在不透明的桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用画树状图(或列表)的方法列出所有等可能的结果,并求两人抽取数字之和是偶数的概率.17. 某单位党支部在“精准扶贫”活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗.已知每棵乙种树苗的价格比甲种树苗的价格贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同,求甲、乙两种树苗每棵的价格.18. 如图,在四边形中,已知平分 , , 的延长线交的延长线于F, .
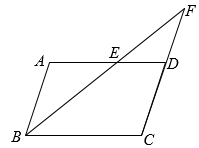 (1)、求证: .(2)、若 , 则的度数是 .19. 某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择其中一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出两幅不完整的统计图,请根据统计图回答问题.
(1)、求证: .(2)、若 , 则的度数是 .19. 某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择其中一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出两幅不完整的统计图,请根据统计图回答问题.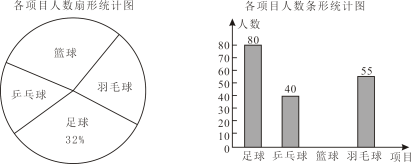 (1)、这次活动一共调查了多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度.(4)、若该学校有3000人,请估计该学校选择乒乓球项目的学生人数约是多少人.20. 图①、图②均是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的三个顶点均在格点上.
(1)、这次活动一共调查了多少名学生?(2)、补全条形统计图.(3)、在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度.(4)、若该学校有3000人,请估计该学校选择乒乓球项目的学生人数约是多少人.20. 图①、图②均是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,△ABC的三个顶点均在格点上.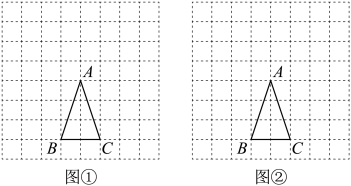 (1)、只用无刻度的直尺,在图①、图②中分别画一个△PBC,使点P在格点上,且∠BPC=∠BAC,所画的两个三角形不全等,不要求写出画法.(2)、 sin∠BPC= .21. 某太阳能热水器水箱的最大水量为160升,在没有放水的情况下匀速注水.已知水箱的蓄水量y(升)与注水时间x(分)之间有如表对应关系.
(1)、只用无刻度的直尺,在图①、图②中分别画一个△PBC,使点P在格点上,且∠BPC=∠BAC,所画的两个三角形不全等,不要求写出画法.(2)、 sin∠BPC= .21. 某太阳能热水器水箱的最大水量为160升,在没有放水的情况下匀速注水.已知水箱的蓄水量y(升)与注水时间x(分)之间有如表对应关系.x(分)
0
4
8
12
y(升)
20
60
100
140
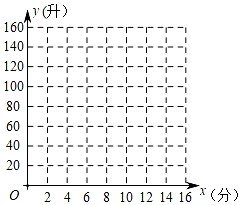 (1)、①建立平面直角坐标系,如图,横轴表示注水时间x,纵轴表示水箱的蓄水量y,描出以表格中数据为坐标的各点.
(1)、①建立平面直角坐标系,如图,横轴表示注水时间x,纵轴表示水箱的蓄水量y,描出以表格中数据为坐标的各点.②观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.
(2)、应用上述发现的规律解决下列问题:①注水时间达到9分钟,水箱的蓄水量为多少升?
②按上述速度注满水箱,需要多少分钟?
22.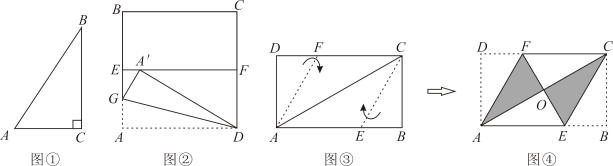 【感知】如图①,中, , , 易知(不需要证明).(1)、【探究】如图②,四边形是一张边长为2的正方形纸片,E、F分别为、的中点,沿过点D的折痕将纸片翻折,使点A落在上的点A'处,折痕交于点G,求的度数和的长.(2)、【拓展】若矩形纸片按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),若 , 直接写出的长.23. 如图,在矩形中, , , 点E为边的中点.动点P从点A出发,沿射线以每秒1个单位长度的速度运动,当点P不与点A重合时,连接 . 作点A关于直线的对称点 , 连接、 , 设点P的运动时间为秒.
【感知】如图①,中, , , 易知(不需要证明).(1)、【探究】如图②,四边形是一张边长为2的正方形纸片,E、F分别为、的中点,沿过点D的折痕将纸片翻折,使点A落在上的点A'处,折痕交于点G,求的度数和的长.(2)、【拓展】若矩形纸片按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),若 , 直接写出的长.23. 如图,在矩形中, , , 点E为边的中点.动点P从点A出发,沿射线以每秒1个单位长度的速度运动,当点P不与点A重合时,连接 . 作点A关于直线的对称点 , 连接、 , 设点P的运动时间为秒.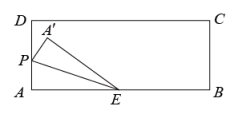 (1)、线段的长为 .(2)、用含t的代数式表示线段的长.(3)、当时,求t的值.(4)、当点在矩形内部(不包括边界)时,直接写出的取值范围.24. 在平面直角坐标系中,已知某二次函数的图象同时经过点、、 . 其中, .
(1)、线段的长为 .(2)、用含t的代数式表示线段的长.(3)、当时,求t的值.(4)、当点在矩形内部(不包括边界)时,直接写出的取值范围.24. 在平面直角坐标系中,已知某二次函数的图象同时经过点、、 . 其中, .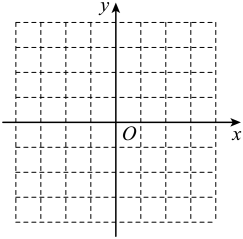 (1)、当时.
(1)、当时.①该二次函数的图象的对称轴是直线 ▲ .
②求该二次函数的表达式.
(2)、当时,若该二次函数的最大值为4,求m的值.(3)、若同时经过点A、B、C的圆恰好与x轴相切时,直接写出该二次函数的图象的顶点坐标.