山西省晋中市太谷区2023年中考一模数学试题

试卷更新日期：2023-04-06 类型：中考模拟

进入出卷网下载

一、单选题

1. -1010的倒数是（）

A、 $1010$ B、 $\frac{1}{1010}$ C、 $- \frac{1}{1010}$ D、 $- 1010$

查看试题解析
2. 下列运算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{6}$ B、 $a^{3} + a^{3} = 2 a^{6}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$

查看试题解析
3. 如图， $A B$ 为 $⊙ O$ 的直径， $A B = 10$ $c m$ ， C、D为 $⊙ O$ 上两点，若 $∠ B C D = 60 °$ ，则 $B D$ 的长为（）

A、 $5 c m$ B、 $5 \sqrt{3} c m$ C、 $\frac{5}{2}$ $c m$ D、 $\frac{5}{2} \sqrt{3}$ $c m$

查看试题解析
4. 若式子 $\frac{1}{\sqrt{2 x - 4}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x < 2$

查看试题解析
5. 受本土疫情波及全国多数省份，线下餐饮、购物、出行等消费需求减少等影响， $2022$ 年，消费市场持续承压，但必需类商品及汽车销售情况依旧良好，前 $11$ 个月，社会消费品零售总额 $399190$ 亿元，同比下降 $0.1 %$ ，数据 $399190$ 亿用科学记数法表示为（）

A、 $39.919 \times 1 0^{12}$ 元 B、 $3.9919 \times 1 0^{12}$ 元 C、 $3.9919 \times 1 0^{14}$ 元 D、 $3.9919 \times 1 0^{13}$ 元

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x - 3 < 0 \\ 4 - x > - 5 \end{array}$ 的解集是（）

A、 $x < \frac{3}{2}$ B、 $\frac{3}{2} < x < 9$ C、 $x > \frac{3}{2}$ D、 $x < 9$

查看试题解析
7. 寒假期间王华坚持每天在家做跳绳训练，他记录了最近一周的成绩（个/分）：157、159、160、162、160、163、164，该组数据的中位数和众数分别为（）

A、162、160 B、160、162 C、160、160 D、159、160

查看试题解析
8. 在三边都不相等的 $△ A B C$ 的边 $A B$ 上有一点D，过点D画一条直线，与三角形的另一边相交所截得的三角形与 $△ A B C$ 相似，这样的直线最多可以画（）

A、5条 B、4条 C、3条 D、2条

查看试题解析
9. 如图，在同一平面直角坐标系中，一次函数 $y_{1} = k x + 3$ （k是常数，且 $k \neq 0$ ）与反比例函数 $y_{2} = \frac{6}{x}$ 的图象交于 $A (- 3 ， - 2)$ ， $B (2 ， m)$ 两点，则不等式 $k x + 3 > \frac{6}{x}$ 的解集是（）

A、 $- 3 < x < 2$ B、 $x < - 3$ 或 $x > 2$ C、 $- 3 < x < 0$ 或 $x > 2$ D、 $0 < x < 2$

查看试题解析
10. 如图，在边长为4的正六边形 $A B C D E$ 中，先以点B为圆心， $A B$ 的长为半径作 $\overset{⌢}{A C}$ ，再以点A为圆心， $A B$ 的长为半径作 $\overset{⌢}{B P}$ 交 $\overset{⌢}{A C}$ 于点P，则图中阴影部分的面积为（）

A、 $4 \sqrt{3} + \frac{8 π}{3}$ B、 $4 \sqrt{3}$ C、 $4 \sqrt{3} - \frac{8 π}{3}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

11. ${(\sqrt{3} - 1.732)}^{0} + {(- \frac{1}{4})}^{- 2} =$ ．

查看试题解析
12. 将抛物线 $y = x^{2} - 4 x - 1$ 化成顶点式为．

查看试题解析
13. 一个不透明的袋子里装有2个白球，2个彩球，这些球除颜色外完全相同，小欢从袋子里随机一次摸出2个球，摸到两个都是彩球的概率是．

查看试题解析
14. 某公园内有一矩形步道，其地面使用相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成．如图表示此步道的地砖排列方式，其中步道上总共使用84个三角形地砖，那么连续排列的正方形地砖总共有个．

查看试题解析
15. 如图，点P是双曲线 $y = \frac{2}{x} (x > 0)$ 上的一点，过点P作y轴的平行线交直线 $A B$ ： $y = \frac{1}{4} x - 1$ 于点Q，连接 $O P 、 O Q$ ．当点P在曲线上运动，且点P在Q的上方时，则四边形 $O A Q P$ 面积的最大值是．

查看试题解析

三、解答题

16.

(1)、计算： $\frac{\sqrt{3}}{3} t a n 60 ° + \frac{1}{2} c o s 30 ° s i n 30 ° + s i n^{2} 45 °$ ．

(2)、先化简： $\frac{3 x + 1}{x + 2} - \frac{2 x}{x^{2} - 4} \div \frac{x}{x^{2} - 4 x + 4}$ ，然后选择一个适当的、你喜欢的数代入求值．

查看试题解析
17. $2023$ 年元旦期间，面对新型肺炎疫情的侵袭，全国上下众志成城，我们坚信在党中央的统一领导下必定打赢这场没有硝烟的战争． $1$ 月 $3$ 日，为了增强学生对此次疫情的了解与防控，某学校在本校网站上开展了相关知识的宣传教育活动． $1$ 月 $13$ 日为了解这次宣传活动的效果，学校在校网站上从全校 $1500$ 名学生中随机抽取若干名在线学生进行知识测试（测试满分 $100$ 分，得分均为整数），并根据这若干人的测试成绩，制作了如下不完整的统计图表．
学生知识测试成绩的频数表

成绩a（分）
频数（人）
$A$
$50 \leq a < 60$
$10$
$B$
$60 \leq a < 70$
$15$
$C$
$70 \leq a < 80$
$m$
$D$
$80 \leq a < 90$
$40$
$E$
$90 \leq a \leq 100$
$15$
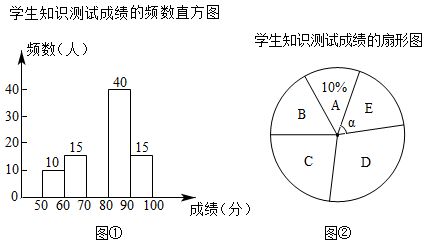
由图表及统计图中给出的信息，回答下列问题：

(1)、本次抽取的样本容量是 ▲ ；扇形 $E$ 的圆心角 $α =$ ▲ $°$ ，并补全频数直方图；

(2)、如果 $80$ 分以上（包括 $80$ 分）为优秀，请估计全校 $1500$ 名学生中成绩优秀的人数．

(3)、针对这次活动谈谈你的想法．

查看试题解析
18. 乡村振兴战略总方针中提出，生态宜居是提高乡村发展质量的保证．生态宜居其内容涵盖村容整洁，村内水、电、路等基础设施完善，以保护自然、顺应自然、敬畏自然的生态文明理念．“村村通”公路政策是国家构建和谐社会、支持新农村建设，实现生态宜居的一项重大公共决策，是一项民心工程。某工程队承接了60万平方米的乡村筑路工程，由于情况有变，……设原计划每天筑路的面积为x万平方米，列方程为： $\frac{60}{(1 - 20 %) x} - \frac{60}{x} = 30$ ，

(1)、根据方程在下列四个选项中选择省略的部分是（）

A、实际工作时每天的工作效率比原计划提高了 $20 %$ ，结果提前30天完成了这一任务 B、实际工作时每天的工作效率比原计划提高了 $20 %$ ，结果推迟30天完成了这一任务 C、实际工作时每天的工作效率比原计划降低了 $20 %$ ，结果推迟30天完成了这一任务 D、实际工作时每天的工作效率比原计划降低了 $20 %$ ，结果提前30天完成了这一任务

(2)、在（1）的条件下，在下列两个选项中任选一项作为问题，写出完整的解题过程．
E．求：实际每天筑路的面积是多少万平方米？
F．求：原计划完成这项筑路工程需要多少天？
我选的问题是： ▲

查看试题解析
19. 如图，在△ABC中，AB＝AC， $∠ B A C < 90 °$ ，以AB为直径作⊙O分别交BC，AC于点D，E，连接AD，过点D作⊙O的切线交AC于点F．

(1)、试猜想 $\overset{⌢}{B D}$ 和 $\overset{⌢}{E D}$ 的数量关系，并说明理由．

(2)、若 $A B = 5 \sqrt{2} ， A D = 2 \sqrt{10}$ ，求AF的长．

查看试题解析

20. 通过学习《解直角三角形》这一章，王凯同学勤学好问，在课外学习活动中，探究发现，三角形的面积、边、角之间存在一定的数量关系，下面是他的学习笔记．请仔细阅读下列材料并完成相应的任务．

在 $△ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别为a、b、c， $△ A B C$ 的面积为 $S_{△ A B C}$ ，过点A作 $A D ⊥ B C$ ，垂足为D，则在 $R t △ A B D$ 中，

∵ $s i n B = \frac{A D}{A B}$

∴ $A D = A B \cdot s i n B$

∴ $S_{△ A B C} = \frac{1}{2} B C \cdot A D = \frac{1}{2} B C \cdot A B \cdot s i n B = \frac{1}{2} a c s i n B$

同理可得， $S_{△ A B C} = \frac{1}{2} b c s i n A$ ， $S_{△ A B C} = \frac{1}{2} b a s i n C$

即 $S_{△ A B C} = \frac{1}{2} b c s i n A = \frac{1}{2} a c s i n B = \frac{1}{2} b a s i n C$ ……………①

由以上推理得结论：三角形的面积等于两边及其夹角正弦积的一半．

又∵ $a b c \neq 0$

∴将等式 $\frac{1}{2} b c s i n A = \frac{1}{2} a c s i n B = \frac{1}{2} b a s i n C$ 两边同除以 $\frac{1}{2} a b c$ ，得， $\frac{s i n A}{a} = \frac{s i n B}{b} = \frac{s i n C}{c}$

∴ $\frac{a}{s i n A} = \frac{b}{s i n B} = \frac{c}{s i n C}$ …………………②

由以上推理得结论：在一个三角形中，各边和它所对角的正弦的比值相等．

理解应用：如图，甲船以 $30 \sqrt{2}$ 海里/时的速度向正北方向航行，当甲船位于A处时，乙船位于甲船的南偏西75°方向的B处，且乙船从B处沿北偏东15°方向匀速直线航行，当甲船航行20分钟到达D处时，乙船航行到甲船的南偏西60°方向的C处，此时两船相距 $10 \sqrt{2}$ 海里．

(1)、求：

△ A D C

的面积；

(2)、求：乙船航行的速度（结果保留根号）．

查看试题解析

21. 光明中学校园有一升旗台，旗杆的高度引起了爱思考的同学们的极大兴趣．数学活动小组的同学对旗杆的高度进行了测量．测量方法如下：如图，从旗杆底部分别向东、西走到达点A、C处，在A，C两处分别放置学生制作的高为 $1.2 m$ 的测倾仪，在A处测得旗杆顶端Q的仰角是 $60 °$ ，在C处测得旗杆顶端Q仰角为 $50 °$ ，点A，C及旗杆 $P Q$ 在同一平面内，旗杆底部P与点A，C在同一条直线上， $A C = 10 m$ ，根据测量小组提供的数据，求该旗杆的高度．
（结果精确到 $0.1 m$ ，参考数据： $s i n 50 ° \approx 0.77$ ， $c o s 50 ° \approx 0.64$ ， $t a n 50 ° \approx 1.2$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
22. 综合与探究
问题情境：
数学活动课上，老师给出如下基础模型：如图①，已知 $R t △ A B C$ ， $∠ A C B = 90 °$ ，过点C任作一条直线l（不与 $C A 、 C B$ 重合），过点A作 $A D ⊥ l$ 于点D，过点B作 $B E ⊥ l$ 于点E，当点A、B在直线l同侧时，易证 $△ A C D ∽ △ C B E$ （下列解题可直接用此结论）．

(1)、如图②，当点A、B在直线l异侧时，求证： $△ A C D ∽ △ C B E$ ．

(2)、模型应用：在平面直角坐标系中，已知直线l： $y = k x - 4 k$ （k为常数， $k \neq 0$ ）与x轴交于点A，与y轴的负半轴交于点B，以AB为边、B为直角顶点作直角三角形 $A B C$ 且 $t a n ∠ A C B = 2$ ．若直线l经过点 $(2 ， - 3)$ ，当点C在第三象限时，点C的坐标为．

(3)、若点D是函数 $y = 2 x (x < 0)$ 图象上的点，且 $B D ∥ x$ 轴，当点C在第四象限时，连接 $C D$ 交y轴于点E，求点C、D的坐标（用含k的式子表示）及 $B E$ 的长．

查看试题解析
23. 综合与探究
如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 2 ， 0)$ ， $B (6 ， 0)$ 两点，与y轴交于点C，且 $O C = 6$ ，点D是抛物线上第一象限内的一个动点，设点D的横坐标为m．连接 $A C 、 B C 、 D B 、 D C$ ．

(1)、求抛物线的函数表达式；

(2)、过点D作与y轴的平行线的直线l，与 $B C$ 交于点E，当 $△ C D E$ 是以 $D E$ 为底边的等腰三角形时，求点D的坐标．

(3)、若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

	成绩a（分）	频数（人）
$A$	$50 \leq a < 60$	$10$
$B$	$60 \leq a < 70$	$15$
$C$	$70 \leq a < 80$	$m$
$D$	$80 \leq a < 90$	$40$
$E$	$90 \leq a \leq 100$	$15$